
- •Задания 10: вычисление значений выражений, включающих степени, радикалы, логарифмы и тригонометрические функции Вычисление значения логарифмического выражения
- •Вычисление значения числового выражения
- •Вычисление значения числового выражения, включающих степени
- •Вычисление значения числового выражения, включающих радикалы (корни)
- •Вычисление значения тригонометрического выражения
- •Знаки тригонометрических функций
- •Формулы приведения
Вычисление значения числового выражения, включающих радикалы (корни)
|
Основные свойства корней:
Если
п 1.
2.
3.
4.
5.
|
|
Задание 10. Найдите значение
выражения
Решение:
Используя формулы
В бланк ответов: 3 |
Пример 33.
Пример 34.
Задание 10. Найдите значение
выражения
Решение: Используя свойство корней , получим:
В бланк ответов: 4 |
Пример 35.
Задание 10. Найдите значение
выражения
Решение: Используя свойства степеней , , получим:
В бланк ответов: 4 |
Вычисление значения тригонометрического выражения
Для любого х справедливы равенства: |
|||
sin(-x) = - sinx |
cos(- x) = cosx |
tg(- х) = - tgx |
ctg(- х) = - ctgx |
sin(x+2πn) = sinx |
cos(x+2πn ) = cosx |
tg (x+πn) = tgx |
ctg (x+πn) = ctgx |
n – произвольное целое число |
|||
Знаки тригонометрических функций
II I 0 х
III IV
|
+ + 0 х 0 - -
|
у
- + 0 х 0 - +
|
у
- + 0 х 0 + -
|
|
Координатные четверти |
Знаки синуса |
Знаки косинуса |
Знаки тангенса и котангенса |
|
0 х 0 III IV
|
sinα
tgα, ctgα |
cosα
|
Чтобы знать знаки тригонометрических функций, достаточно запомнить фигуру в виде стрелки (рисунок справа). Координатные четверти на стрелке показаны на рисунке слева, их запомнить очень просто и легко. |
|
Знак « + » тригонометрических функций. |
|
|||


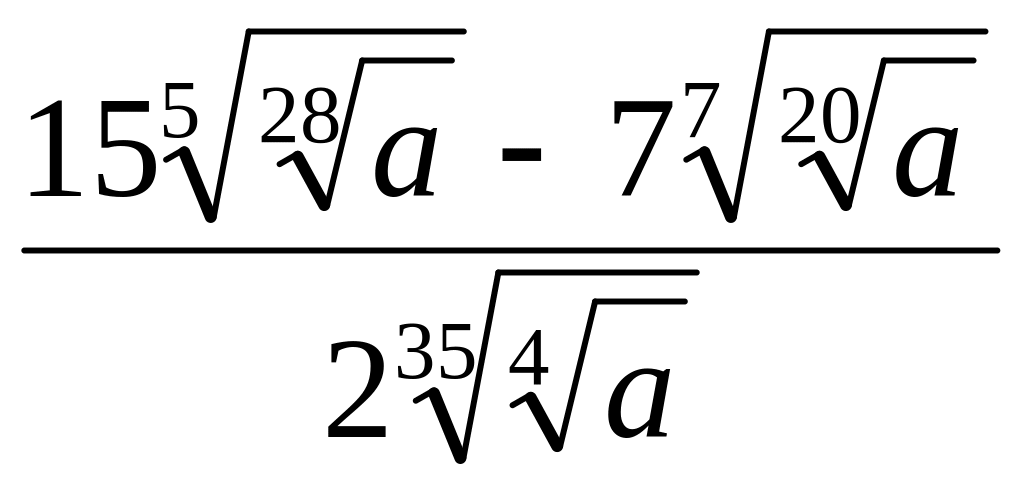 при а > 0.
при а > 0.
 При т = 64
При т = 64
 у
у
 у
у у
у

 II I
II I