2.2.2 Построение графика переходного процесса

Построение графика переходного процесса (рис. 9) в системе по средствам программной среды MathCAD. Так как исходное уравнение имеет вид (13.2), то дифференцирование входного сигнала x(t)=1(t) в правой части уравнения приведет к бесконечно большой величине, что повлечет за собой ошибку в программной среде. Чтобы решение уравнения стало возможным, структуру системы следует преобразовать в виду, показанному на рис. 8. Такое преобразование приводит к тому, что исходное уравнение (13.2) распадается на два уравнения (13.3) [1]:

Рис.8. Преобразованная структура системы

Новой структуре соответствует система уравнений [1]:

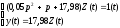(13.3)

Первое уравнение является дифференциальным, второе – алгебраическим, так как содержит производные, находимые из первого уравнения.

Для построения графика переходного процесса (рис. 9) необходимо решить дифференциальное уравнение:

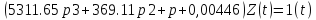
(13.4)

При численном решении дифференциального уравнения n-го порядка преобразуем в систему из n уравнений первого порядка. Для этого выполняем подстановку вида:

z(t)=z₁(t), z^’(t)=z₂(t) (13.5)

В результате подстановки можно записать систему уравнений следующего вида:

(13.6)

Для решение системы в MathCAD необходимо указать следующие параметры:

Исходное уравнение:

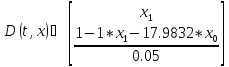(13.7)

Решение дифференциального уравнения методом Рунге-Кутта:

(13.8)

где: - начальные условия.

n – 2000 число точек решения; tk = 200 конечное время решения; D – исходное уравнение.

конечный результат для вычисления переходного процесса.

(13.9)

Представим найденные значение в таблице 5.

Таблица 5 Расчет точек переходного процесса

Расчет точек для графика переходного процесса представим в таблице 6.

Таблица 6. Расчет точек для графика переходного процесса

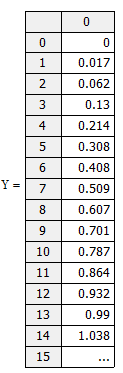
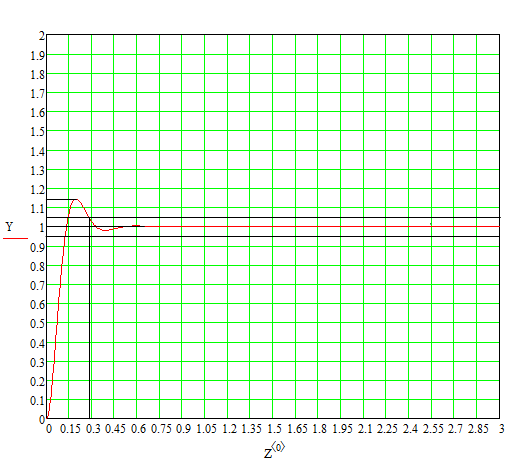
Рис. 9. График переходного процесса системы

2.2.3 Оценка качества исследуемой системы

По графику переходного процесса и по логарифмической характеристики системы производим оценку качества исследуемой системы, приведенной к устойчивости. Для оценки пользуемся следующими показателями:

1. Вид переходного процесса

2. Длительность переходного процесса

3. Величина перерегулирования

4. Запас устойчивости системы по фазе

5. Запас устойчивости системы по амплитуде

Согласно графику переходного процесса (рис.9) переходный процесс имеет колебательный периодический характер.

Длительность переходного процесса для системы удовлетворительного качества должна лежать в пределах:

< t_пп < (13.10)

По графику на чертеже КР-2068.998-26-07-00.00.000.Д. лист1 определяем частоту среза: ω_с=18 оценим время переходного процесса: 0,17< t_пп <0,70

Длительность переходного процесса определим как время, прошедшие от начала переходного процесса (t=0) до момента установления величины выходного сигнала, отличающейся не более чем на 5% от установившегося значения. По графику переходного процесса определяем его длительность: t_пп = 0,28 с.

Это значение удовлетворяет границам оценочного времени переходного процесса.

Величина перерегулирования определяется из соотношения (в процентах):

σ = · 100% =· 100% = 14 %, (13.11)

где: ,- наибольшее и установившееся значения выходного параметра, определяемые по графику переходного процесса (рис.9). Величина перерегулирования не должна превышать 20%, полученное значение удовлетворяет данному условию.

Запасы устойчивости системы, определяемые по логарифмическим характеристикам, характеризуют степень устойчивости системы.

Запас устойчивости системы по фазе определяется через фазовый угол системы на частоте среза ω_с:

(13.12)

где: - фазовый сдвиг, определяем по графику на чертеже КР-2068.998-26-07-00.00.000.Д. лист1

φ_з =180⁰ – 135⁰ = 45⁰

Что бы система обладала достаточным качеством, запас устойчивости по фазе должен лежать в пределах 20˚- 50˚. Система удовлетворяет этому условию.

Запас устойчивости по амплитуде определяется по графику на чертеже КР-2068.998-26-07-00.00.000.Д. лист1 как ордината ЛАХ на частоте фазового угла, равного π:

(13.13)

L_з = -52 дБ

Запас по амплитуде должен быть не менее |15|дБ. В данной системе запас по амплитуде равен -72дБ.