2.1.3. Привидение системы к астатизму

Для того чтобы статическая ошибка системы была равна 0, необходимо привести систему к астатизму, это осуществляется путем добавления интегрального регулятора. передаточная функция регулятора равна [2]

W(p)=k/p (7) где k=10^(L(1)/20)=1

Логарифмическая характеристика системы представлена на чертеже

КР-2068.998-26-07-00.00.000.Д. лист1

2.1.4 Исследование влияния параметров на устойчивость системы.

Исследование проводится методом D – разбиений, и область устойчивости строится в плоскости двух задаваемых параметров системы: постоянная времени объекта управления T_о и коэффициент усиления объекта k_о. Для выполнения исследования необходимо найти характеристический комплекс системы. Для этой цели характеристический полином системы (8) системы преобразуется таким образом, что вместо числовых значений исследуемых параметров в него бы вошли их буквенные обозначения (9):

С(p) = (T_о×p+1)p + k_о·k_им·k_д· k_р (8)

C(p) = (T_о×p+1)p + k_о×15,12 (9)

Преобразуем характеристический полином в характеристический комплекс подстановкой p=jω [1]:

G(jω) = (T_о×jω+1) jω + k_о×15,12 (10)

Запишем условия для граничной устойчивости системы:

(11)

Решив систему уравнений граничной устойчивости найдем параметрические уравнения границы области устойчивости.

(12)

K=0, T=∞

Используем условия устойчивости:

с₀=0 и с₂=0, что дает T_о=0 и k_о=0.

Область устойчивости в соответствии с полученными выражениями показана на рис.7.

рис. 7 Область устойчивости

Правило штриховки. Для его применения найдем определитель[1]:

(12.1)

(12.2)

Таким образом,

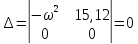
Следовательно, определитель положителен для положительных частот и штриховка должна вестись от кривой при движении по ней в сторону возрастания частот.

Для проверки построений на графике нанесем точку (k_о,Т_о) (зависящие от ω). Примем точку А с координатами (1.18; 0,05); точка принадлежит полученной области устойчивости, следовательно область устойчивости построена верно.

2.2 Исследование качества системы

2.2.1 Уравнение переходного процесса в системе

Передаточная функция замкнутой системы [2]:

Ф(р) = , (13)

где: А(р) и С(p) – степень полинома от p, тогда дифференциальное уравнение системы в операторной форме будет иметь вид:

С(p)·y(p) = A(p)·x(p), (13.1)

где: р - оператор дифференцирования; y(p)- выходной сигнал системы; x(t)- входное воздействие.

Входным воздействием принимается единичная ступенчатая функция x(t) = 1(t), а выражение С(p) подставим из (13), А(р) принимаем равным К. Тогда уравнение системы(13.1) примет следующий вид:

(0.05p²+p+17.98) *y(t)=17.98х(t) (13.2)