2.1.6 Пилкоподібне коливання

З подібними коливаннями завжди маємо справу в пристроях розгортки телевізорів та осцилографів рис. 2.7, а також в пристроях автоматичного регулювання. Оскільки дана функція є непарною, ряд Фур’є для неї має тільки синусні складові.

Знайдемо загальний вираз для коефіцієнтів ряду, враховуючи, що на відрізку

,

де - постійна амплітуда

. (2.14)

Після перетворення отримаємо

(2.15)

З виразу очевидно, що (2.16)

Враховуючи те, що амплітуди синусних гармонік , а початкові фази .

Тоді остаточний вигляд ряду Фур’є для даного сигналу

(2.17)

Графіки амплітудного й фазового спектрів такого коливання показані на рис. 2.8.

2.1.7 Неперіодичні сигнали

Будь-який неперіодичний сигнал можна розглядати як періодичний, період зміни якого дорівнює нескінченності. У зв’язку з цим розглянутий раніше спектральний аналіз періодичних процесів може бути узагальнений і на неперіодичний сигнал.

Розглянемо як буде змінюватись спектр неперіодичного сигналу при необмеженому збільшенні періоду зміни сигналу. При збільшенні періоду Т інтервали між суміжними частотами в спектрі сигналу і амплітуди спектральних складових зменшується і в границі при стають нескінченно малими величинами. При цьому спектральний розклад неперіодичного сигналу відображається рядом Фур’є.

Комплексна форма неперіодичного сигналу має вигляд

. (2.18)

де - спектральна щільність сигналу, - амплітудно-частотна характеристика сигналу, - фазочастотна характеристика сигналу.

Попередній вираз називається формулою зворотного перетворення Фур’є.

Представлення неперіодичної функції інтегралом Фур’є можливо при виконанні таких умов:

1. Функція задовольняє умову Діріхле;

2. Функція абсолютно інтегрована

. (2.19)

Таким чином, спектр неперіодичного сигналу на відміну від спектра періодичного сигналу є суцільним і являє собою суму нескінченної кількості гармонічних складових із нескінченно малими складовими.

Амплітуди гармонічних складових можуть бути представлені у вигляді

, (2.20)

звідки спектральна щільність визначається виразом

. (2.21)

Спектральна щільність пов’язана з функцією часу через пряме перетворення Фур’є

. (2.22)

Спектральна щільність однозначно відображає неперіодичний сигнал і задовольняє умови:

1. ;

2. Модуль спектральної щільності є парною, а аргумент непарною функцією частоти

. (2.23)

2.1.8 Спектр експоненціального імпульсу

Експоненціальний імпульс визначається функцією та приведений на рис. 2.9

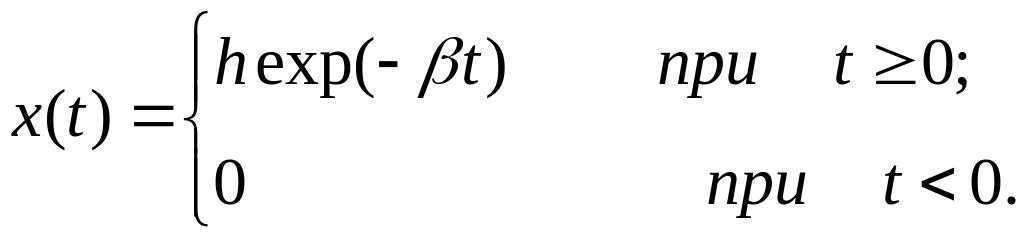(2.24)

модуль і фаза спектральної щільності визначаються відповідно виразами

, (2.25)

де h – початковий рівень сигналу.

На рис. 2.10 приведені графіки модуля і фази спектральної щільності й експоненціального імпульсу.

2.1.9 Спектр сигналу ввімкнення

Сигнал ввімкнення Рис. 2.11 визначається функцією

(2.26)

де – величина сигналу ввімкнення.

Одинична функція 1(t) не задовольняє умову абсолютного інтегрування, тому до неї не можна застосувати перетворення Фур’є. Однак її можна розглядати як утворення з імпульсу експоненціальної форми при необмеженому зменшенні його коефіцієнта затухання . У відповідності з цим спектральна щільність сигналу ввімкнення буде дорівнювати

. (2.27)

Звідки модуль і фаза спектральної щільності визначаються

. (2.28)

Модуль і фаза спектральної щільності сигналу ввімкнення приведені на рис. 2.12.