Тесты

Теория принятия решений.

1. Каноническая задача ЛП.

Каноническая форма задачи характеризуется тремя признаками:

1. Однородная система ограничений в виде системы уравнений;

2. Однородные условия неотрицательности, распространяющиеся на все переменные, участвующие в задаче;

3. Минимизация (максимизация) линейной функции

2. Критерий оптимальности симплекс-метода для решения задачи ЛП на максимум (минимум).

Для задачи на максимум (минимум) коэффициенты в целевой функции в симплекс-таблице неотрицательны (неположительны).

3. Критерий неограниченности целевой функции в симплекс-методе для решения задачи ЛП на максимум (минимум).

Для задачи на максимум существует для которого ,

для задачи на минимум существует для которого .

4. Содержательный смысл оптимального решения вспомогательной задачи в симплекс-методе.

Если оптимальное значение вспомогательной задачи больше нуля, то исходная задача не имеет решений, если оптимальное значение вспомогательной задачи равно нулю, то исходная задача записана в специальной форме с выделенным базисом .

5 . Двойственная задача к задаче ЛП.

6 . Матричная игра, как пара двойственных задач.

7.Задача ЛП для первого игрока.

8.Задача ЛП для второго игрока.

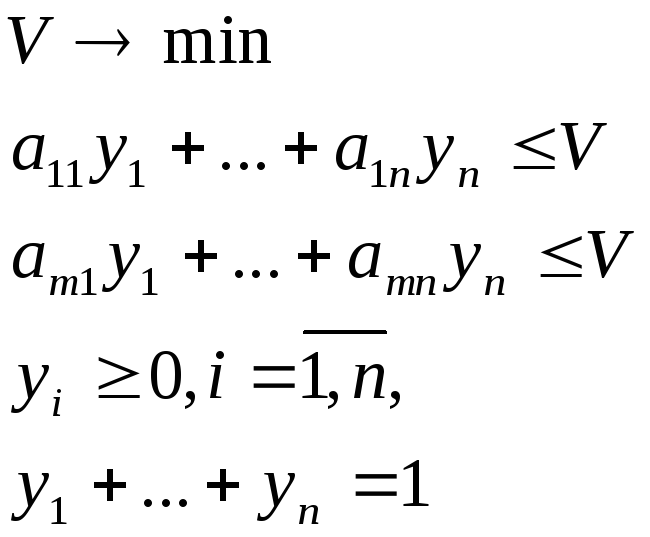
9. Матричная игра «Производство - Рынок».

10. Функция выигрыша для матричной игры «Производство – Рынок».

1 1. Задача о назначениях как задача ЛП.

12. Оценка числа итераций в задаче о назначениях.

Число итераций меньше, либо равно , где -число работ.

13. Уравнение Беллмана.

F_k*(ξ_k­1)=max(ƒ_k(u_k)+F_k+1*(ξ_k))

14.Уравнение Беллмана для задачи с мультипликативным критерием.

F_k*(ξ_k­1)=max (ƒ_k(u_k)F_k+1*(ξ_k))

15.Уравнение Беллмана для задачи распределения ресурсов.

F_k*(ξ_k­1)=max(ƒ_k(u_k)+F_k+1*(ξ_k­1-x_k))

16.Уравнение Беллмана для задачи о замене оборудования.

φ(t)­p+ƒ(0)-r(0) - F_k+1(1)¸ если u= «заменить»

F_k*(t )=

{

ƒ(t)- ƒ(t)-r(t) - F_k+1(t+1)¸ если u= «сохранить»

17.Обобщенная задача Лагранжа.

18. Выбор направления S_K в методе покоординатного спуска.

S_kє{±(0,...,l...)}

19. Нахождение шага α_к в методе наискорейшего спуска.

ƒ(x^k+αS^k)=φ(α)

φ (α)→ min

20. Выбор направления S_K в методе сопряженных градиентов.

2 1. Каноническая задача для задачи выпуклого программирования:

2 2. Нахождение направления в методе возможных направлений.

2 3. Нахождение шага в методе возможных направлений.

24. Последовательная оптимизация для лексикографического подхода решения задачи многокритериальной оптимизации .

Решаем последовательность задач:

1.

2.

25. Симметрическая задача ЛП .