Сравнение выборочных средних
П ри проведении экспериментальных исследований схема опыта часто строится так, что образуются две сопоставимые группы – опытная и контрольная (например, средний вес животных опытной и контрольной групп, средняя продуктивность дочерей двух производителей или двух выборок, составленных из особей разных пород). При этом проводят сравнение прежде всего по величине средних арифметических, полученных для каждой группы, для чего вычисляют разность между этими средними, т.е. D = Х1 – Х2.
По величине разности делают вывод о различиях сравниваемых групп. Но нужно еще определить, достоверна ли эта разность или она случайна. Для этого вычисляют ошибку разности (md):
md
=
и находят критерий достоверности разности (td):
td
=
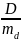
Полученное фактическое значение td сравнивают с табличным критерием Стьюдента (табл. 5) при необходимом уровне вероятности (Р), взятом для соответствующего числа степеней свободы (ν = n1+n2 – 2). При большом числе степеней свободы (ν > 100) о достоверности показателя ориентировочно можно судить по последующим значениям:
при td = 3,29 разность достоверна в 999 случаях из 1000 (99,9%),
при td = 2,58 разность достоверна в 99 случаях из 100 (99%),
если величина td меньше 1,96, то разность между средними сравниваемых групп не может быть признана достоверной.
т.е. принимая Р равным 0,95, риск сделать ошибку составляет 5% или 1 на 20 вариант. При вероятности Р = 0,99 риск ошибиться равен 1% (1 раз из 100) и т.д.
Пример. Изучается эффективность влияния микроэлементов при откорме бычков. С этой целью взяты две группы (опытная и контрольная) по 14 животных с одинаковой средней живой массой в каждой. Откармливают их при использовании одинаковых рационов, лишь в рационы животных опытной группы включены микроэлементы.
П о окончании опыта и обработки первичных данных получены следующие результаты: средняя масса (Х1) животных опытной группы 300 кг, контрольной (Х2) – 260 кг. Средние ошибки по опытной и контрольной группам соответственно равны: Sх1 = 9 кг, Sх2 = 6 кг. Достоверно ли различие по массе животных опытной и контрольной групп?
Подставляем значения средних арифметических и их ошибок в формулу:
td
=
=
=
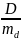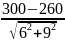= 3,7
Значение вероятности, соответствующее найденному td, определяем по таблице Стьюдента (табл. 5). Для этого устанавливаем, прежде всего, число степеней свободы (v). В данном примере (сравнение двух выборок) v = n1 + n2 – 2 = 14 + 14 – 2 =26. Находим в таблице строку v = 26. Из трёх стандартных значений t, находящихся в этой строке, выбираем число, равное или превышающее установленное в нашем опыте (td = 3,7). Такое число стоит в последней графе. Верхняя строка этой графы показывает искомую вероятность – Р = 0,999.
Следовательно, разность – d = 40 кг, полученную в данном примере, можно считать высокодостоверной (Р ≤ 0,001).
Таблица 5 - Значение критерия достоверности td по Стъюденту
При трех уровнях вероятности р
Число степеней свободы (v)
|
Уровень вероятности (Р) |
||
0,95 |
0,99 |
0,999 |
|
1 |
12,71 |
63,66 |
636,6 |
2 |
4,30 |
9,93 |
31,60 |
3 |
3,18 |
5,84 |
12,94 |
4 |
2,78 |
4,60 |
8,61 |
5 |
2,57 |
4,03 |
6,86 |
6 |
2,45 |
3,71 |
5,96 |
7 |
2,37 |
3,50 |
5,41 |
8 |
2,31 |
3,36 |
5,04 |
9 |
2,26 |
3,25 |
4,78 |
10 |
2,23 |
3,17 |
4,59 |
11 |
2,20 |
3,11 |
4,44 |
12 |
2,18 |
3,06 |
4,32 |
13 |
2,16 |
3,01 |
4,22 |
14 |
2,15 |
2,98 |
4,14 |
15 |
2,13 |
2,95 |
4,07 |
16 |
2,12 |
2,92 |
4,02 |
17 |
2,11 |
2,90 |
3,97 |
18 |
2,10 |
2,88 |
3,92 |
19 |
2,09 |
2,86 |
3,88 |
20 |
2,09 |
2,85 |
3,85 |
21 |
2,08 |
2,83 |
3,82 |
22 |
2,07 |
2,82 |
3,79 |
23 |
2,07 |
2,81 |
3,77 |
24 |
2,06 |
2,80 |
3,75 |
25 |
2,06 |
2,79 |
3,73 |
26 |
2,06 |
2,78 |
3,71 |
27 |
2,05 |
2,77 |
3,69 |
28 |
2,05 |
2,76 |
3,67 |
29 |
2,05 |
2,76 |
3,66 |
30 |
2,04 |
2,75 |
3,65 |
35-39 |
2,03 |
2,72 |
3,59 |
40-44 |
2,02 |
2,70 |
3,55 |
45-60 |
2,01 |
2,66 |
3,50 |
70-100 |
1,98 |
2,63 |
3,39 |
120 и > |
1,96 |
2,58 |
3,29 |
|
Р ≤ 0,05* |
Р ≤ 0,01** |
Р ≤ 0,001*** |
Задание 13. По приведенным ниже данным определить, существуют ли достоверные породные различия в активности ферментов крови коров (табл. 6).
Т аблица 6 - Активность ферментов крови коров в среднем за лактацию, (Х ± Sх)
-
Порода
n
Амилаза (%)
Щелочная фосфатаза (мг%Р)
Айрширская
17
12,86 ± 0,35
2,32 ± 0,19
Голландская
20
13,75± 0,35
2,17 ± 0,15
Чёрно - пестрая
18
10,37 ± 0,47
1,85 ± 0,14
Задание 14. По приведенным ниже данным определить достоверность разности содержания лейкоцитов (тыс.) в 1 мм3 крови здоровых и больных пневмонией овец.
Таблица 7 – Содержание лейкоцитов в крови овец
-
Здоровые
5,8
6,2
8,3
6,0
9,8
7,4
7,2
8,6
7,7
8,0
Больные
12,0
12,1
11,8
11,4
11,5
11,1
13,6
10,5
12,7
13,0
З адание 15. Рассчитать значения Х, Sх в группах бройлерных петушков в возрасте 6 суток, используя нижеприведенные данные (табл. 8). Определить достоверность разницы (td) показателей в контрольной и опытных группах при включении в рацион повышенных дозировок аскорбиновой кислоты в предстартерный период. Сделать вывод об эффективности дополнительного введения витамина и оптимальном дозировании его в комбикорм – предстартер.
Таблица 8 - Живая масса петушков в группах с добавлением аскорбиновой
кислоты – АК, (возраст 6 суток), г
-
Контрольная группа
АК – 50 мг/ кг корма
1 опытная
АК – 250 мг/кг корма
2 опытная
АК – 500 мг/кг корма
115; 118; 120; 121; 113;
113; 110; 112; 116; 110;
120; 122; 113; 121; 116;
120; 118; 115; 112; 112;
110; 116; 120; 122; 120;
115; 118; 120; 121; 122;
125; 126; 128; 130; 128;
127; 130; 129; 131; 130;
126; 131; 131; 131; 129;
126; 129; 130; 128; 131;
130; 127; 126; 125; 126;
126; 125; 127; 130; 131;
123; 125; 119; 126; 125;
125; 124; 120; 126; 124;
124; 122; 123; 125; 120;
119; 126; 125; 124; 126;
120; 126; 124; 122; 124;
123; 125; 119; 126; 122;
Задание 16. Определить достоверность различий иммуногематологических показателей петушков при введении аскорбиновой кислоты (табл.9).
Таблица 9 - Иммуногематологические показатели петушков в возрасте