Тема 2 показатели изменчивости признаков в совокупностях
Цель занятия. Изучить методы вычисления показателей изменчивости признаков и применение их в практике селекционной работы.
Содержание занятия. Установление степени изменчивости (вариабельности) признака в популяциях имеет большое значение при ее генетическом анализе и в селекции. Именно по величине изменчивости определяют возможность улучшения стада путем отбора лучших животных.
При изучении изменчивости (вариабельности) признака особей данной совокупности применяют следующие параметры: лимит (lim = Хmax – Xmin), среднее квадратическое отклонение (σ), коэффициент вариации (Сv, %), нормированное отклонение (t).
Лимиты характеризуют минимальное и максимальное значение изучаемого признака в выборочной совокупности и указывают на амплитуду вариации. Чем больше разность между максимальной и минимальной вариантой, тем значительнее изменчивость признака. Однако эти показатели недостаточны, так как особи с такими показателями зачастую бывают нехарактерны для данной популяции. Кроме того, лимиты не отражают степень разнообразия внутри группы. Поэтому в биометрии используют другой показатель, учитывающий отклонения (точнее, их квадраты) каждой варианты от средней арифметической.
Н апример, при одинаковой средней высоте в холке животных двух групп – Х1 = 115 см и Х2 = 115 см – лимиты в первой группе составляли 105 – 125 см, а во второй – 110 – 120 см. Размах колебаний в первой группе – D1= 125 – 105 =20 см, а во второй – D2 =120 – 110 = 10 см. Таким образом, при одной и той же средней группы не однородны.
Наилучшим показателем разнообразия признака является среднее квадратическое отклонение (σ), которое учитывает отклонение каждой варианты от средней арифметической.
Вычисление среднего квадратического отклонения
σ (сигма) – среднеквадратическое отклонение, показывает насколько в среднем каждая варианта отклоняется от Х ; чем больше варьирует признак, тем больше σ. Вся изменчивость признака укладывается от средней арифметической в пределах ± 3σ (правило плюс-минус трех сигм), поэтому средняя арифметическая, уменьшенная или увеличенная на 3σ, дает практически крайние варианты признака. Так, при нормальном распределении особей совокупности в пределы ±3σ входит 99,7% особей. Около 95% особей входит в пределы ± 2σ и приблизительно 68% особей - в пределы ±1σ. Например, если σ удоя коров за лактацию равна 520 кг, а Х = 4000 кг, то минимальный удой коров в такой совокупности, вероятнее всего, будет равен 2440 кг = (Х - 3σ = 4000 – (3 × 520) , а максимальный – 5560 кг = (Х + 3σ = 4000 + (3 × 520).
При небольшом числе вариант среднее квадратическое отклонение вычисляется по формуле:
;
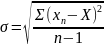при малой выборке
;
при большой выборке
г де Σ(хn – Х)2 – сумма квадратов отклонений вариант от средней арифметической совокупности.
Пример. Вычислить среднее квадратическое отклонение по данным о живой массе при рождении десяти поросят из помета одной свиноматки (табл. 2).
Таблица 2 – Вычисление среднего квадратического отклонения прямым способом (при малом числе вариант)
-
Живой вес
поросят (кг),
х
Отклонения
х - Х
Квадраты отклонений
( х – Х)2
1,2
- 0,15
0,0225
1,5
+ 0,15
0,0225
1,1
- 0,25
0,0625
1,3
- 0,05
0,0025
1,4
+ 0,05
0,0025
1,3
- 0,05
0,0025
1,4
+ 0,05
0,0025
1,4
+ 0,05
0,0025
1,3
- 0,05
0,0025
1,6
+ 0,25
0,0625
Σ х = 13,5
Σ (х-Х) = 0
Σ (х-Х)2 = 0,1850
В первую графу вписывают варианты (живую массу поросят при рождении). Суммировав их и разделив сумму на число вариант, получают среднюю массу поросенка (Х).
Х
=
=
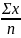= 1,35 кг
З атем надо вычесть Х из каждой варианты и разности (х – Х), т.е. отклонения варианты от средней, вписать во вторую графу. Для проверки правильности вычислений суммируют все разности (х – Х): сумма должна быть равной нулю. Далее каждое отклонение возводят в квадрат и вписывают квадраты отклонений (х – Х)2 в третью графу. В отличие от отклонений, которые могут быть положительными и отрицательными, квадраты отклонений всегда положительны.
Н аконец, просуммировав все показатели третьей графы, получают сумму квадратов отклонений - Σ(х-Х)2, которую вписывают в итоге третьей графы.
Среднее квадратическое отклонение вычисляют по формуле:
=
= ± 0,14
Сигма является показателем разнообразия признака. Согласно правилу трёх сигм, почти все варианты укладываются в интервал от - 3σ до + 3σ. В данном примере масса поросят в генеральной совокупности должна находиться между 1,35 - 3×0,14 и 1,35 + 3×0,14, т.е. между 0,93 и 1,77 кг, что соответствует действительности.
Задание 4. В двух хозяйствах имеется по 10 бычков. В первом хозяйстве их массы равны (кг): 400, 410, 420, 430, 440, 450, 460, 470, 480, 490; во втором – 400, 445, 445, 445, 445, 445, 445, 445, 445, 490. Найти среднюю живую массу бычков, лимиты и средние квадратические отклонения по данным первого и второго хозяйств.
З адание 5. Вычислить Х и σ для следующих выборок:
а) 56, 60, 46, 53, 58, 52, 53, 50, 48, 54;
б) 53, 25, 70, 34, 42, 92, 55, 86, 49, 54.