Тема 1 вычисление средних величин

Цель занятия. Изучить методы вычисления средних величин, используемых в животноводстве.

Содержание занятия. Наблюдения, проводимые над биологическими объектами, могут охватывать всех членов изучаемой совокупности (сплошное наблюдение), а могут ограничиваться обследованием лишь части (выборочное наблюдение). Совокупность из которой отбирается часть – это генеральная совокупность, а отобранная часть – выборка. По выборке судят о состоянии всей генеральной совокупности. Например, нецелесообразно высевать всю партию семян для того, чтобы определить их всхожесть или силу прорастания. Поэтому в большинстве случаев обходятся выборочными наблюдениями (исследованиями).

Количественные показатели (живая масса животных, количество яиц, количество протеина в зерне, удой молока, урожайность зерна и т.п.), которые позволяют судить о качественном своеобразии варьирующих объектов и сравнивать их между собой, называются статистическими характеристиками.

Наиболее важные из них средние величины и показатели вариации признаков.

Средние величины обладают большей устойчивостью, способностью характеризовать группу однородных единиц одним средним числом.

Средняя арифметическая (Х или М) – наиболее распространенный и широко применяемый статистический показатель среднего значения варьирующего признака при количественном его выражении.

Среднюю арифметическую в малочисленных выборках (до 30 особей) вычисляют прямым способом - определяется как сумма всех членов совокупности, делённая на их общее число - n.

Х

где х₁, х₂, х_n – члены совокупности.

Х показывает, какое значение признака наиболее характерно в целом для конкретной совокупности животных.

Например, в группе их 10 коров суточный удой молока отдельных особей составил, кг: 18,4; 15,5; 19,1; 14,4; 18,7; 16; 19,5; 17; 20,1; 17,3. Следовательно, средняя арифметическая для группы коров

Х = = 17,6 кг

Средняя взвешенная (Х_взв) представляет собой результат усреднения средних арифметических нескольких совокупностей. Она вычисляется по формуле:

Х_взв = =

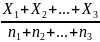г де Х_взв – средняя взвешенная;

Х ₁, Х₂, Х₃…- средние арифметические первой, второй и т.д. совокупностей;

n₁, n₂, n₃ – объем этих совокупностей.

Пример. Требуется вычислить среднюю жирность молока, полученного от коровы за первый квартал, по приведенным ниже данным (табл.1).

Таблица 1 – Данные о содержании жира в молоке и удоях коровы

Месяцы	Средняя жирность м олока (Х), %	Удои (n), кг
Январь	4,0	350
Февраль	3,8	400
Март	4,0	450

Средняя взвешенная за квартал равна:

Х _взв = 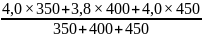= 3,93%

Задание 1. Живая масса поросят свиноматки №1 при рождении (крупноплодность) составила: 1,2; 1,5; 1,0; 1,3; 1,4; 1,3; 0,9; 1,4; 1,3 кг, а поросят свиноматки №2: 1,2; 1,3; 1,0; 0,8; 1,3; 0,9; 1,0; 1,1; 1,2; 1,0 кг.

Вычислить отдельно среднюю живую массу поросят матки №1 и матки №2.

Задание 2. Суточные приросты живой массы в группе телят составили (г): 667, 521, 644, 443, 759, 576, 820, 691, 487, 722. Вычислить среднюю арифметическую приведенного показателя.

З адание 3. Вычислить среднюю живую массу коров по данным трех хозяйств. В первом хозяйстве Х₁ =380 кг, n₁ = 1000; во втором Х₂ = 460, n₂ = 500; в третьем Х₃ = 400, n₃ = 2000.