2.6 Задания по задаче о назначениях

Решить задачу о назначениях с матрицей:

2.1		2.2
2.3		2.4
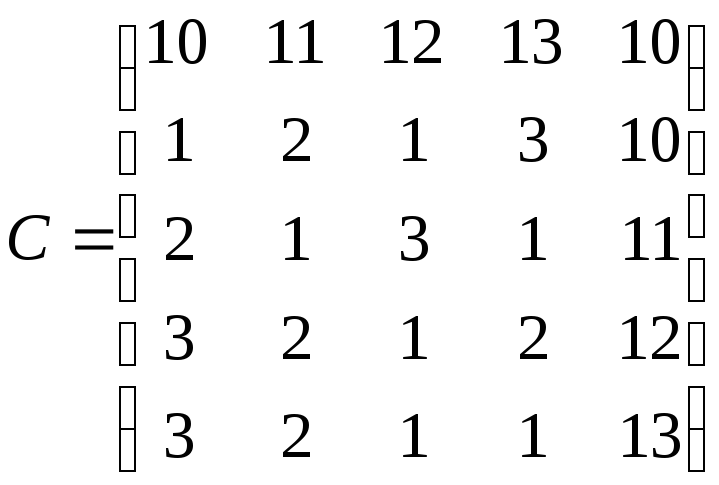
2.5		2.6
2.7		2.8
2.9		2.10
2.11		2.12
2.13		2.14
2.15		2.16
2.17		2.18
2.19		2.20
2.21		2.22
2.23		2.24
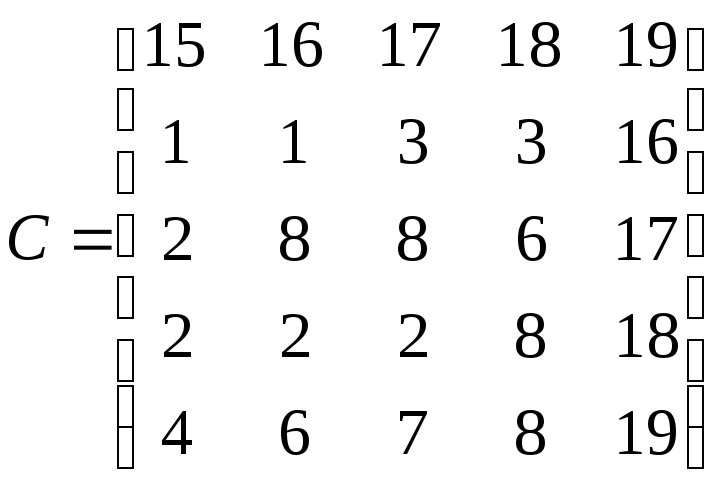
2.25		2.26
2.27		2.28
2.29		2.30

3. Задача о коммивояжере

3.1 Постановка задачи

Имеется nгородов. Расстояния между любой парой городов известны и составляют:. Если между городамиiиjнет дороги, то. По тем же соображениям. Вообще говоря,(путь в одну сторону не обязательно совпадает с путем, пройденным в обратную сторону). Коммивояжер, выезжая из какого-либо города, должен посетить все города, побывав в каждом из них ровно один раз, и вернуться в исходный город. Объезд городов, удовлетворяющий этим требованиям, называется маршрутом коммивояжера. Необходимо определить маршрут минимальной длины, понимая под длиной маршрута сумму длин входящих в него дуг.

3.2 Математическая модель

Для каждой пары городов iиjвведем переменную, которая может принимать следующие значения:

Тогда длина маршрута вычисляется по формуле:

.

Ограничения задачи:

, (3.1)

(3.2)

интерпретируются следующим образом. Уравнения (3.1) характеризуют то требование к маршруту, что въезжать в каждый город jможно ровно один раз; уравнения (3.2) обеспечивают ровно один выезд из каждого городаi. Однако этих условий недостаточно для полного описания маршрутов, так как возможны неполные обходы городов, к примеру, как на рисунке

Поэтому для исключения подциклов необходимо добавить следующее условие: пусть S– некоторое подмножество данного множества городов,– остальные города. Так как коммивояжер должен объехать всеnгородов, то во всяком его маршруте должна присутствовать хотя бы одна дуга с началом в множествеSи с концом в множестве. Аналитически это требование можно записать так:

для любогоS.(3.3)

Таким образом, математической моделью задачи коммивояжера является следующая задача целочисленного линейного программирования:

(3.4)

при ограничениях (3.1), (3.2), (3.3) и

,(3.5)

–целочисленные,.(3.6)