2.5.Метод Гомори

Метод Гомори для нахождения целочисленного решения относится к большой группе методов, называемых методами отсечений. Эти методы основаны на введении в задачу дополнительных ограничений, позволяющих учесть требование целочисленности. Основная идея методов отсечений состоит в том, что на полученное оптимальное нецелочисленное решение накладывается дополнительное ограничение, которое делает это решение недопустимым, но и не отсекает ни одного целочисленного решения от области допустимых решений.

2.5.1.Методы отсечения и их сущность

Рассмотрим общую задачу целочисленного программированияв постановке:

_, назовем эту задачу — задачей.

Задача без учета целочисленности:

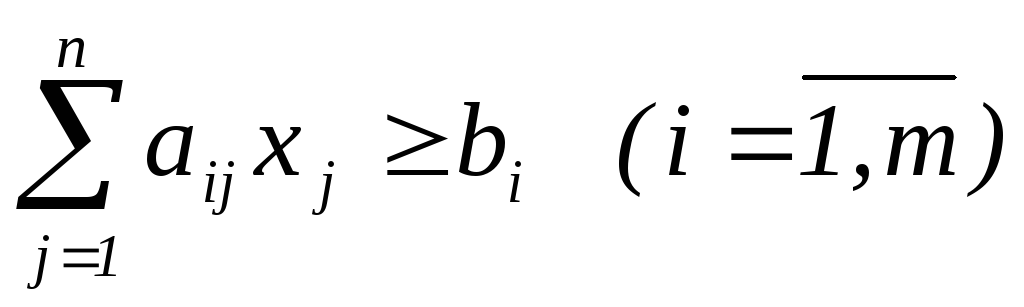
_, назовем -задачей.

Теорема:

Пусть G- многогранник, -множество его целых точек, R- выпуклая линейная

оболочка множества , тогда:

1. -целочисленный многогранник;

2. ;

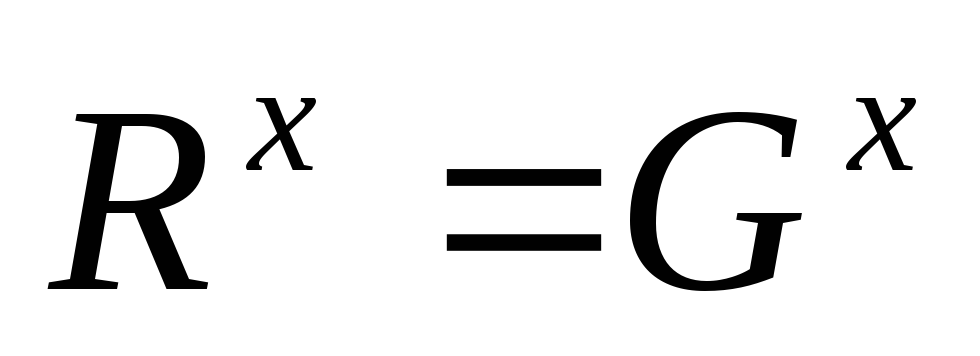3. - множество опорных планов задачи содержится в

2.5.2.Общий алгоритм метода Гомори

Правильное отсечение - отсечение, которое удовлетворяют следующим требованиям:

1. линейно;

2. отсекает часть области, не содержащей допустимых решений

целочисленной задачи

3. не отсекает ни одного целочисленного оптимального плана.

Этапы решения:

1. Решается -задача, соответствующая исходнойзадаче.

Если -задача не имеет решения, т.е. G пуста или неограниченна в положительном направлении возрастания (убывания) F, то устанавливается неразрешимость целочисленной задачи.

2. Оптимальное решение -задачи проверяется на целочисленность.

Если решение целочисленное, то задача решена.

В противном случае, если условие целочисленности не выполняется хотя бы по одной координате, то переходят к третьему этапу.

1. Дополнительное ограничение, которое

1. линейно;

2. отсекает часть области, не содержащей допустимых решений целочисленной - задачи;

3. не отсекает ни одного целочисленного оптимального плана, который входит в систему ограничений..

Шаг 0.Пусть оптимальная таблица имеет вид:

	b		…
L			…
			…
…	…	…………..
/			…

Среди элементов – есть дробные числа.

Шаг 1.Среди дробных компоненттаблицы выбираем элементс максимальной дробной частьюи по строкеiсоставляем дополнительное ограничение:

Здесь - целая часть числа(наибольшее целое число, не превышающее число).

Шаг 2.Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

Замечания:

• Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами.

• На шаге 2 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно потребуется несколько итераций).

• Если на шаге 2 в базис вводится переменная дополнительного ограничения , то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).