2.3 Двойственный симплекс-метод

Метод работает с теми же симплексными таблицами, что и прямой симплекс - метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис.

Вычислительная схема двойственного симплекс – метода

Шаг 0. Начинаем с симплексной таблицы

	B		…
L			…
			…
…	…	…………..
			…

где .

Шаг 1.Проверка на оптимальность. Если, то решение- оптимальное.

Шаг 2.Выбор ведущей строки. Выбираем среди номеровi, для которых, номерkс максимальным по модулю значением

Строка kобъявляетсяведущей.

Шаг 3.Проверка на неразрешимость. Если в строкенет отрицательных элементов, то двойственная целевая функция неограниченна и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.

Шаг 4.Выбор ведущего столбцаs. Выбираем среди отрицательных элементов строкиэлемент с номеромs, для которого выполняется равенство

Столбец sобъявляетсяведущим, а элемент-ведущимэлементом.

Шаг 5.Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).

2.4 Алгоритм метода искусственного базиса

Шаг 1.Приводим задачу ЛП к канонической форме

с неотрицательными правыми частями .

Шаг 2. В каждуюi-ю строку ограничений вводим искусственную неотрицательную переменнуюx_i и строим вспомогательную задачу ЛП вида:

Эта задача имеет допустимое базисное решение . Для этого целевую функцию необходимо выразить через свободные переменные:

Шаг 3. Для построенной вспомогательной задачи строим симплексную таблицу:

	b		…
			…
			…
.	.	…
			…

и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.

Шаг 4. Еслии все переменныеявляются небазисными, тоmпеременных извойдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид:

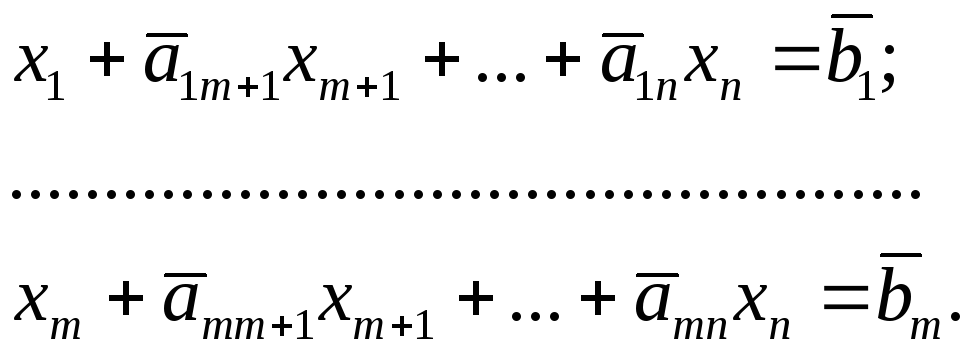
Так как переменные , то их исключили, не нарушив при этом равенств. Выражая целевую функцию основной задачичерез небазисные переменныесистемы, получим исходную задачу.

Шаг 5.Если, но в базисе остались искусственные переменные, для которых, то проводим для каждой искусственной переменной из базиса следующее преобразование симплексной таблицы: выбираем ведущим столбцом столбец такой переменной, для которой элемент индексной строки, а элемент столбца . В этом случае строка искусственной переменнойбудет ведущей и после стандартного преобразования симплексной таблицы (Шаг 6 из прямого симплекс-метода) искусственная переменнаявыведется из базиса. В результате получим симплексную таблицу, соответствующуюШагу 4.

Шаг 6. Если, то допустимого решения в исходной задаче не существует (не могут все искусственные переменныебыть равными нулю), а значит, система ограничений задачи несовместна – процесс решения исходной задачи завершается.