1 Построение математической модели

Цель оптимизации: минимизация убытков от производства костюмов при условии выполнения установленного плана производства.

Составим математическую модель.

1. Параметры задачи:

i - вид костюма( i=1..3)

j – номер цеха (j=1..3)

Пусть x_ij – количество костюмов i-го вида, производимых на j-ом цехе

g_i – стоимость одного костюма i-го вида

a_ij - затраты на производство одного костюма i-го вида в j-ом цехе

d_i – заказ на костюмы i-го вида

2. Составим ограничения, которым должны удовлетворять эти переменные.

Заказ по костюмам i-того вида должен быть выполнен:

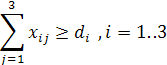
Данная задача относится к классу задач целочисленного линейного программирования, поэтому

Эти ограничения означают, что отрицательное количество костюмов не имеет содержательного смысла, также как и дробное число костюмов.

3. Составим целевую функцию, которая в математической форме, отражает критерий эффективности выбора лучшего варианта.

Так как необходимо составить оптимальный план производства обеспечивающий минимальные расходы, то целевую функцию можно представить в виде разности между расходами на производство всех костюмов и выгодой от их продажи:

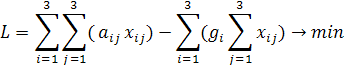
Итак, математическая модель будет иметь вид:

, (i= , j=)

(i= , j=)

2 Теоретическая часть

2.1 Обзор численных методов решения задач лп

Рассмотрим задачу ЛП в канонической форме:

(1)

(2)

(3)

Будем предполагать, что , уравнения системы (2) линейно независимы, m<n и система (2) -(3) совместна.

При сделанных предположениях можно выбрать m неизвестных, таких, чтобы определитель, составленный из коэффициентов при неизвестных, не обращался в ноль. Тогда задача (1)-(3) может быть приведена к виду, который называется специальной формой задачи ЛП:

(4)

Одно из допустимых решений этой задачи можно найти, если переменные положить равными нулю. Такое решение называетсядопустимым базисным решением. Оно имеет вид:

Этому решению соответствует значение целевой функции . Переменныеназываютбазисными, а переменные называютнебазисными или свободными. Число возможных базисов в задаче размерности n с m ограничениями не превосходит величину .

Известно, что каждому допустимому базисному решению соответствует вершина многоугольника допустимых решений, и оптимальное решение задачи достигается в одной из вершин многоугольника. Поэтому оптимальное решение задачи ЛП находится среди допустимых базисных решений. Существуют рациональные способы последовательного перебора допустимых базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальное число. К таким методам относится симплекс-метод. [2].

2.2 Алгоритм симплекс-метода для задачи на минимум

Шаг 0. Приводим задачу ЛП к специальной форме (4).

Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме:

	B		…		…
L			…		…
			…		…
..	..	…………
			…		…
..	..	…………
			…		…

Заметим, что этой таблице соответствует допустимое базисное решение задачи (4). Значение целевой функции на этом решении

Шаг 2. Проверка на оптимальность.

Если среди элементов индексной строки симплекс – таблицы нет ни одного положительного элемента, т. е., оптимальное решение задачи ЛП найдено:.Алгоритм завершает работу.

Шаг 3. Проверка на неразрешимость.

Если среди есть положительный элемент, а в соответствующем столбценет ни одного положительного элемента, то целевая функцияL является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует. Алгоритм завершает работу.

Шаг 4. Выбор ведущего столбца q.

Среди элементов выбираем максимальный положительный элемент.Этот столбец объявляемведущим.

Шаг 5. Выбор ведущей строки p.

Среди положительных элементов столбца находим элемент, для которого выполняется равенство:

Строку p объявляем ведущей. Элемент объявляем ведущим.

Шаг 6. Преобразование симплексной таблицы.

Составляем новую симплекс-таблицу, в которой:

а) вместо базисной переменной записываем, вместо небазисной переменнойзаписываем;

б) ведущий элемент заменяем на обратную величину ;

в) все элементы ведущего столбца (кроме ) умножаем на ;

г) все элементы ведущей строки (кроме ) умножаем на;

д) оставшиеся элементы симплексной таблицы преобразуются по следующей схеме «прямоугольника»: Из элемента вычитается произведение трех сомножителей:

первый - соответствующий элемент ведущего столбца;

второй - соответствующий элемент ведущей строки;

третий - обратная величина ведущего элемента .

Преобразуемый элемент и соответствующие ему три сомножителя как раз и являются вершинами «прямоугольника».

Шаг 7. Переход к следующей итерации осуществляется возвратом к шагу 2.