Задания для самостоятельной работы

Вычислить интегралы:

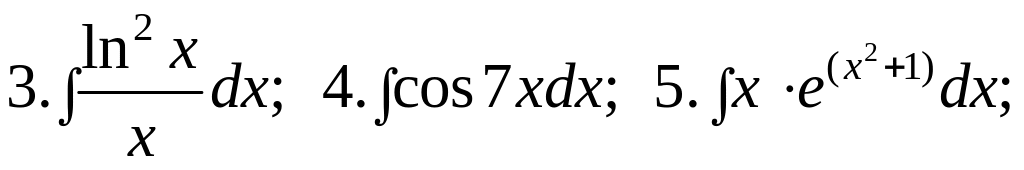
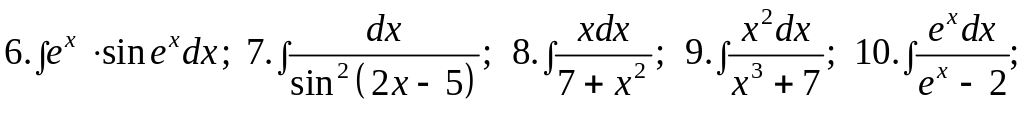
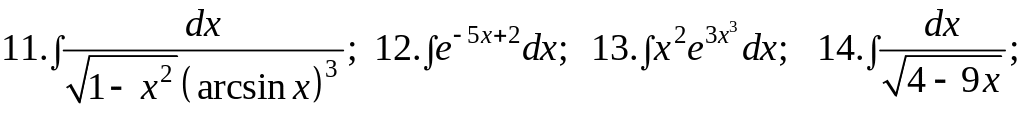
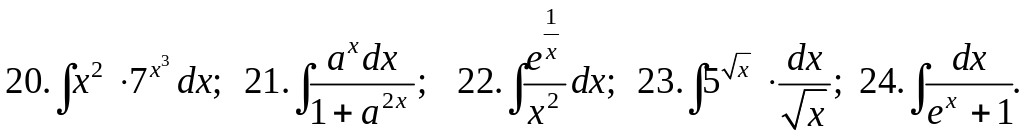
4. Замена переменной (подстановка).

Один из сильнейших приёмов для интегрирования функций – метод замены переменной или подстановки  основан на следующем простом замечании:

если известно, что

,

то тогда

.

Это непосредственно вытекает из правила дифференцирования сложной функции

,

если учесть, что .

Обращаем внимание на то, что при выборе подстановки , которая упростит подынтегральное выражение, в составе последнего должен найтись множитель , дающий дифференциал новой переменной.

Пример 1. Вычислить интеграл .

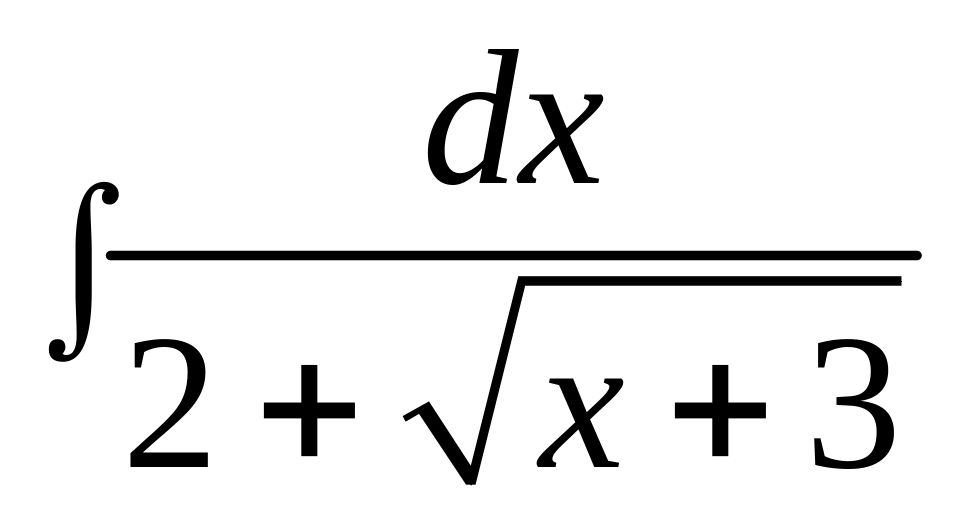Решение. Произведём подстановку, избавляющую подынтгральную функцию от иррациональности: . Получаем

.

Выделим целую часть, вычислим интегралы и сделаем обратную замену :

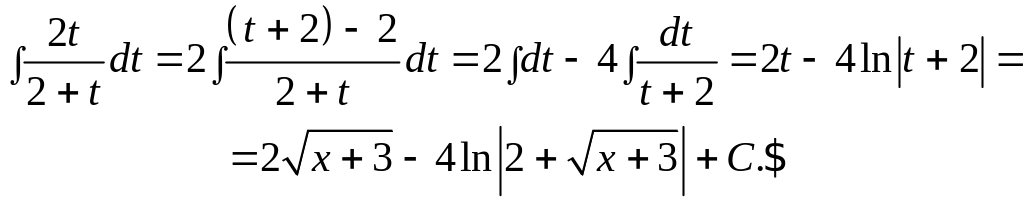
В следующих примерах предлагается сокращённая запись.

Пример 2. Вычислить интегралы a) 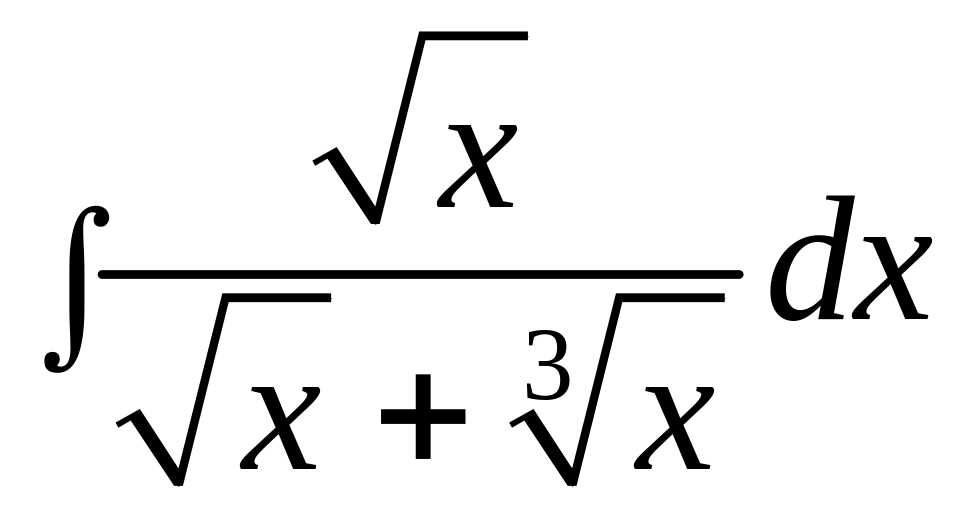; b) .

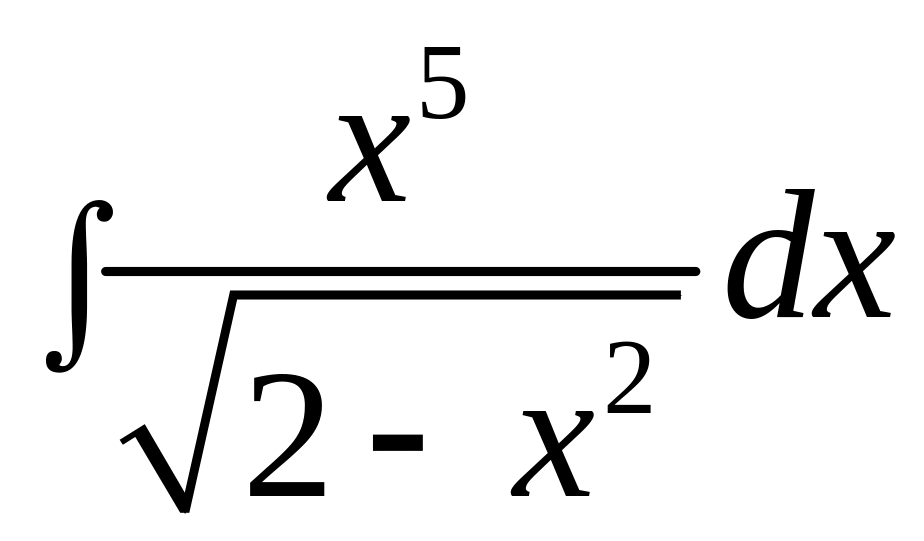Решение.

a) Если сделать замену , то все корни извлекутся, поэтому

.

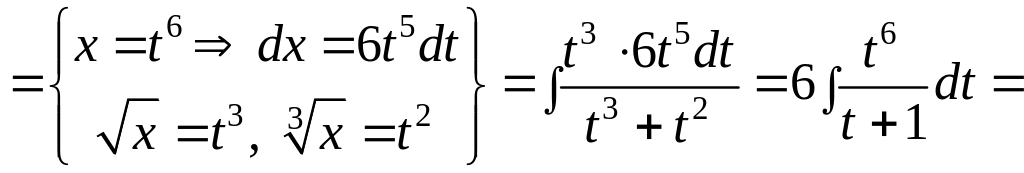
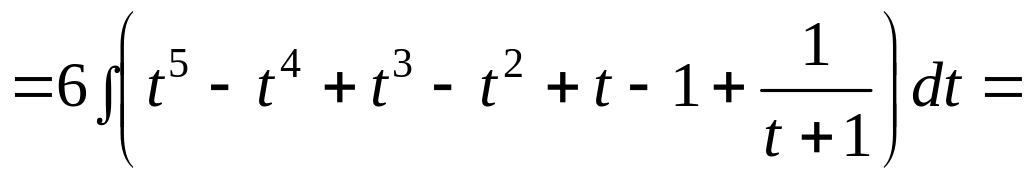
b) Если представить подынтегральное выражение в виде

,

то становится очевидной подстановка . Поэтому

.▼

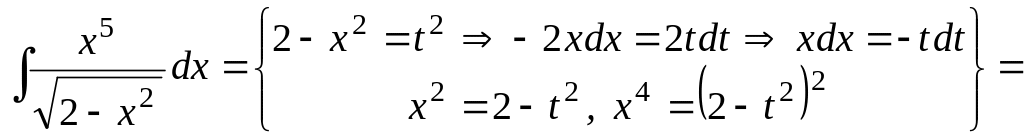
Пример 3. Вычислить интеграл .

Решение. Сначала преобразуем подынтегральное выражение:

.

Теперь вырисовывается подстановка :

.▼

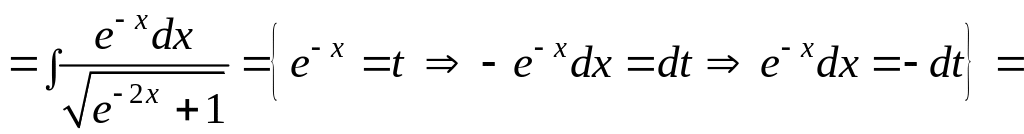
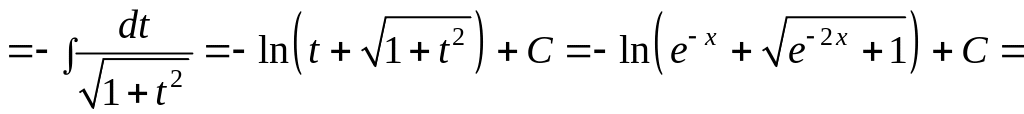
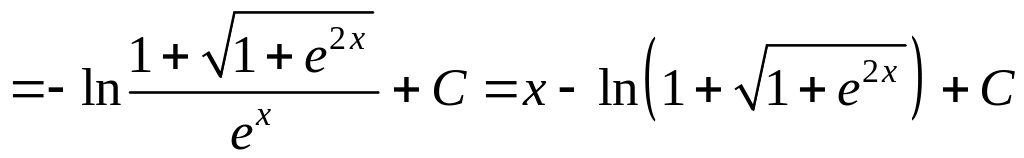Пример 4. Вычислить интегралы a) , b) .

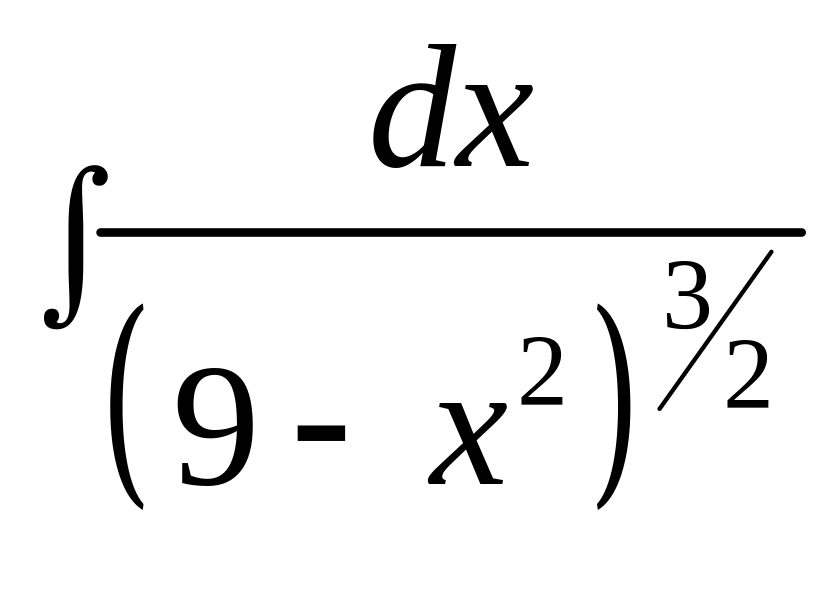Решение. a) Разность квадратов под корнем и основное тригонометрическое тождество подсказывают нам тригонометрическую подстановку (или )

.

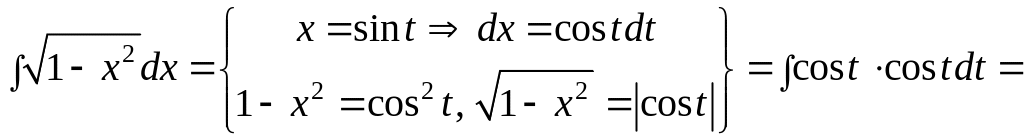
Остаётся произвести обратную замену:

.

Значит, .▼

Замечание. Мы считаем, что переменная изменяется между –1 и 1, а переменная , поэтому , а . Позже, при вычислении определённых интегралов от таких функций надо будет внимательно следить за пределами изменения переменной.

b) В этом случае квадратный корень извлечется, если сделать замену . Тогда

.

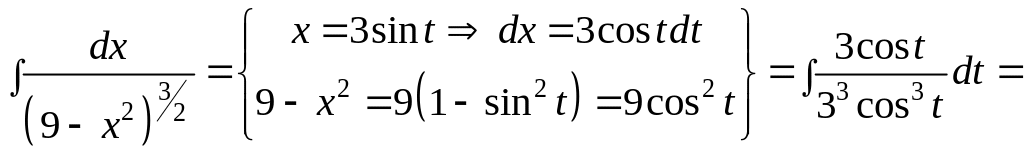
Вернемся к исходной переменной. Т.к. , то

.▼

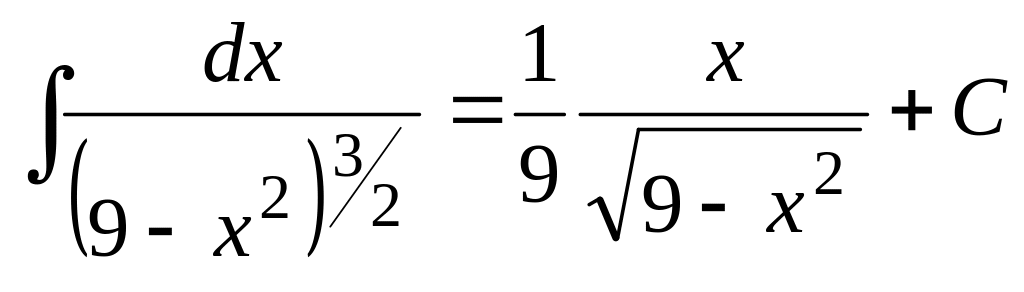Пример 5. Вычислить интегралы a) 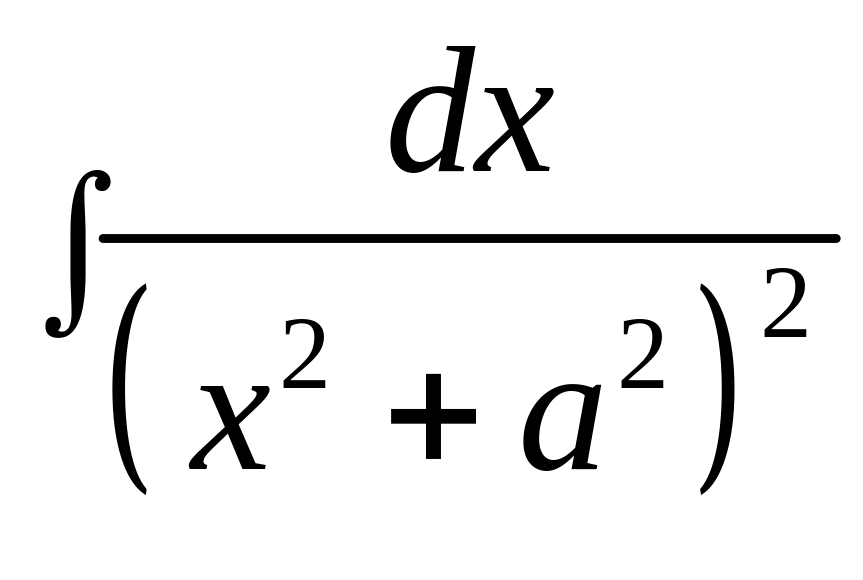, b) .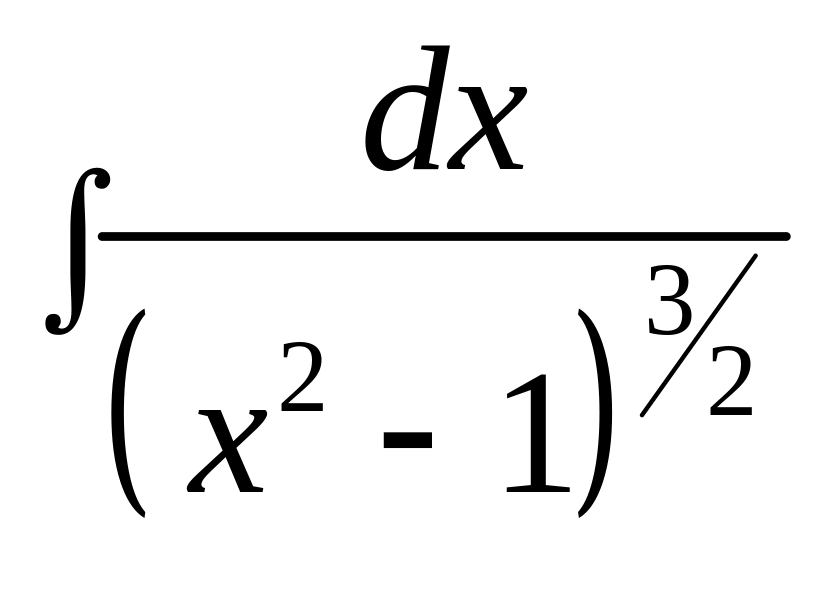

Замену переменной в таких интегралах подсказывает тригонометрическое тождество .

Решение.

a)

.

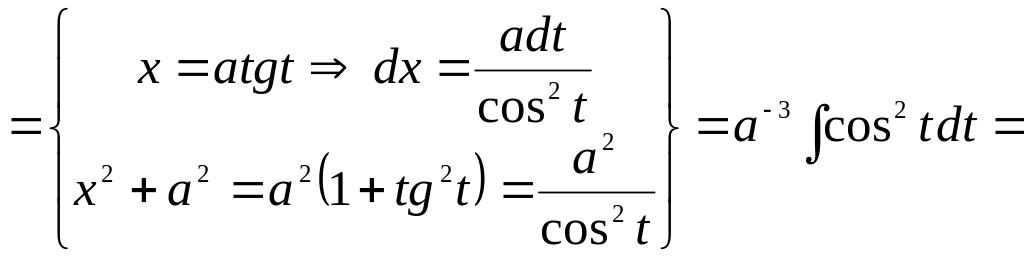
Вернёмся к исходной переменной (по известному тангенсу найдем косинус и синус):

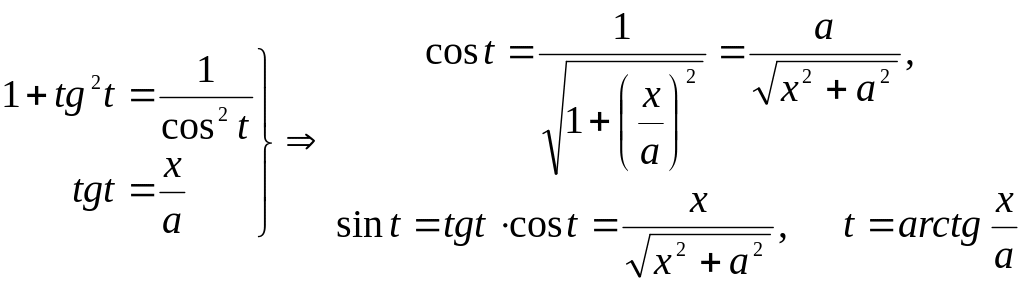
Значит, = .

Позже этот интеграл будет вычислен другим методом.

b) =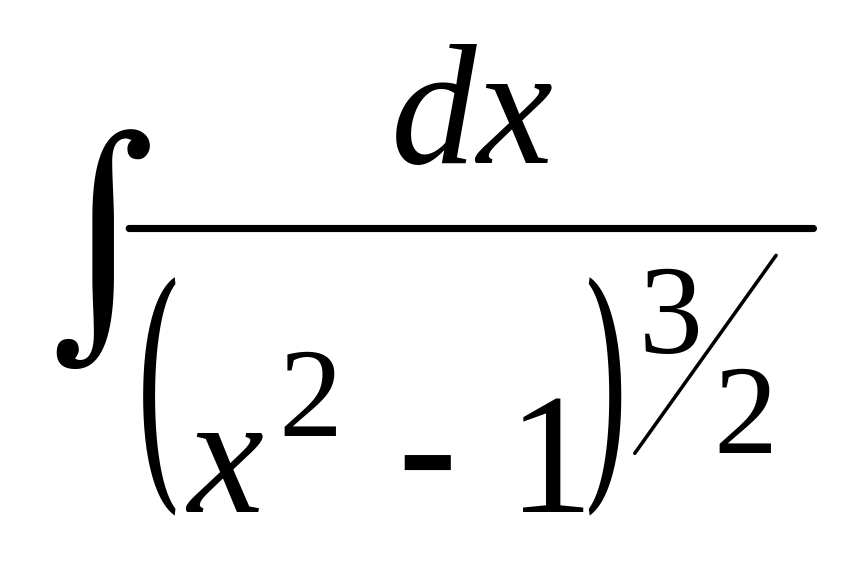

.

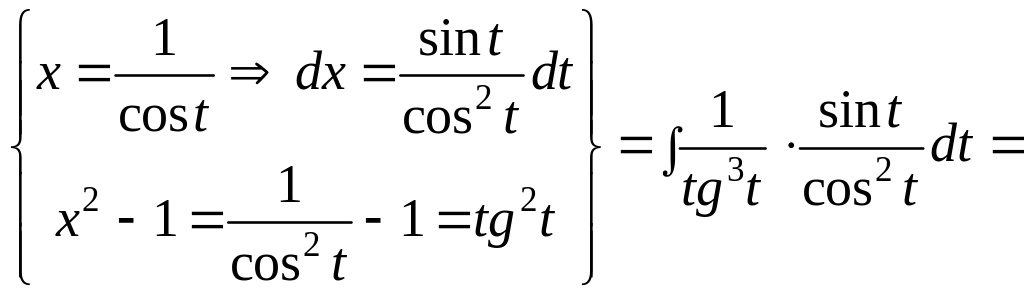
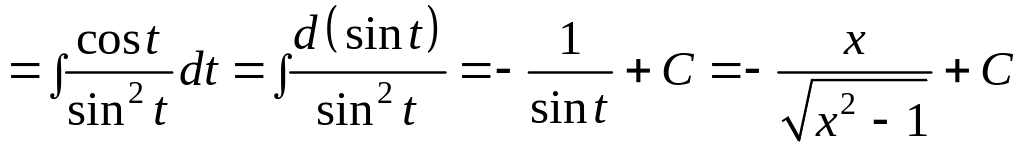Здесь при обратной замене по известному косинусу нашли синус: .▼

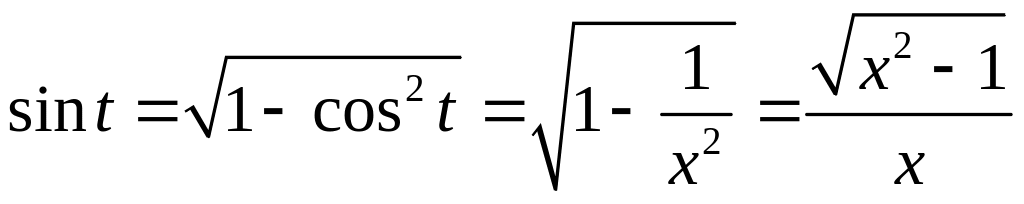Задания для самостоятельной работы

Вычислить интегралы:

; ;

; ;

; ;

; ;

; .

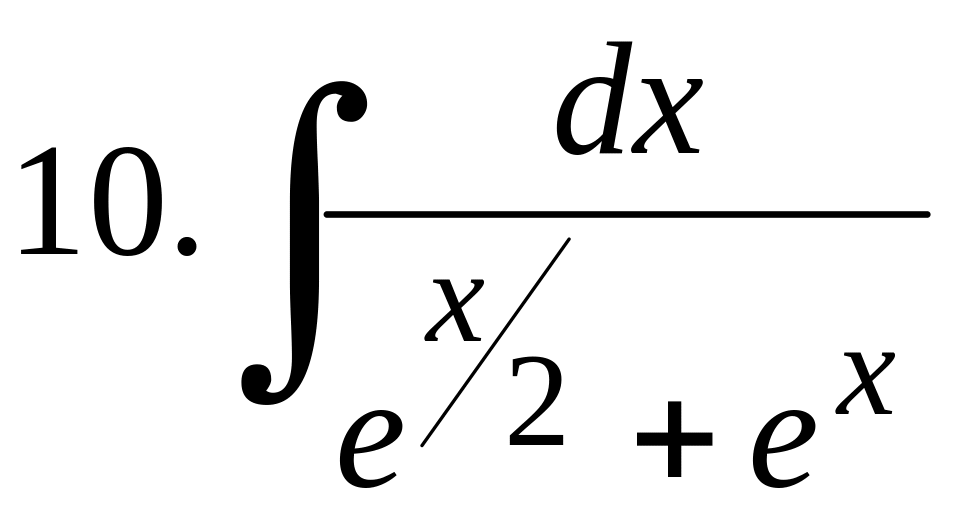5. Интегрирование по частям

Пусть функции и дифференцируемы на некотором множестве и пусть на этом множестве существует первообразная для произведения . Тогда на множестве существует первообразная и для функции , причём справедлива формула

.

Так как , а , то формулу интегрирования по частям можно записать в виде:

. (1)

Формула (1) сводит вычисление интеграла к интегралу . Обращаем внимание на то, что часть интеграла в дальнейшем дифференцируется – справа в формуле (1) мы видим выражение . А часть интегрируется – справа фигурирует функция . Если правильно выбрать части, то получим более простой интеграл (во всяком случае, не более сложный).

Перечислим основные группы интегралов, которые вычисляются методом интегрирования по частям.

1. К первой группе относятся интегралы вида

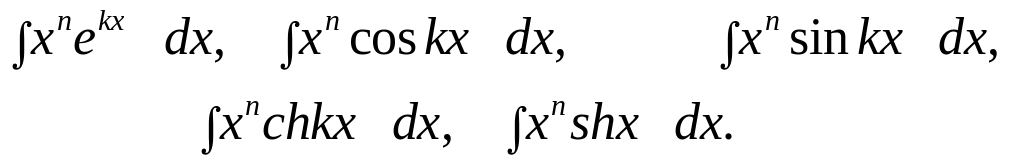
Вместо степенной функции подынтегральное выражение может содержать функцию . Здесь постоянные, натуральное число. Такие интегралы вычисляются с помощью -кратного интегрирования по частям. В качестве части , которую предстоит дифференцировать, следует взять (или ), тогда каждый шаг понижает степень на единицу. А интегрирование части - экспоненты, косинуса или синуса – не изменяет характера этой функции.

Пример 1. Вычислить интеграл

Решение. В соответствии с рекомендациями будем множитель дифференцировать, т.е. положим , а множитель будем интегрировать: .

Предлагаем следующую форму записи:

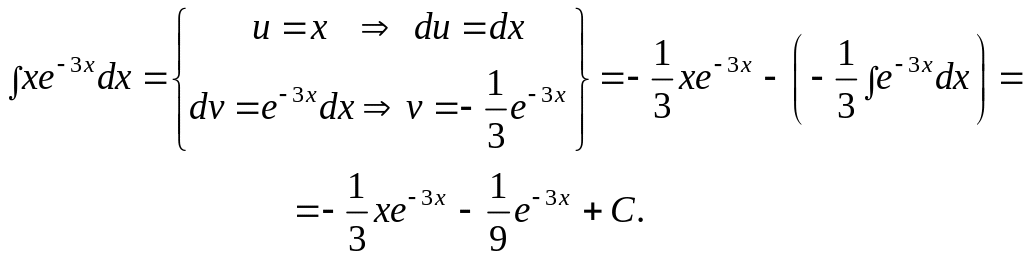
Здесь получили результат после первого шага. ▼

Пример 2. Вычислить интеграл .

Решение.

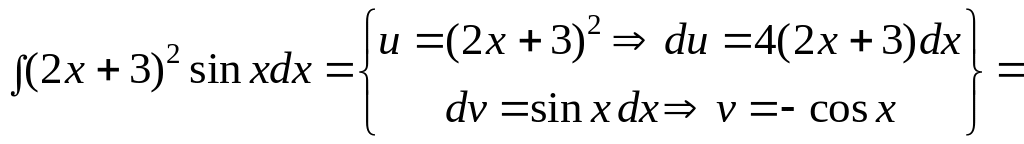
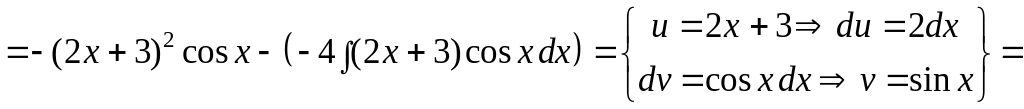
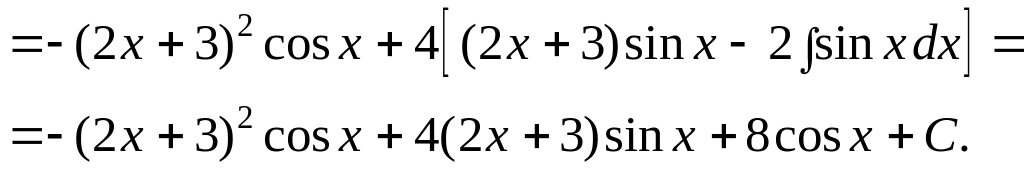
Здесь пришлось дважды интегрировать по частям. ▼

Пример 3. Вычислить интеграл .

Решение.

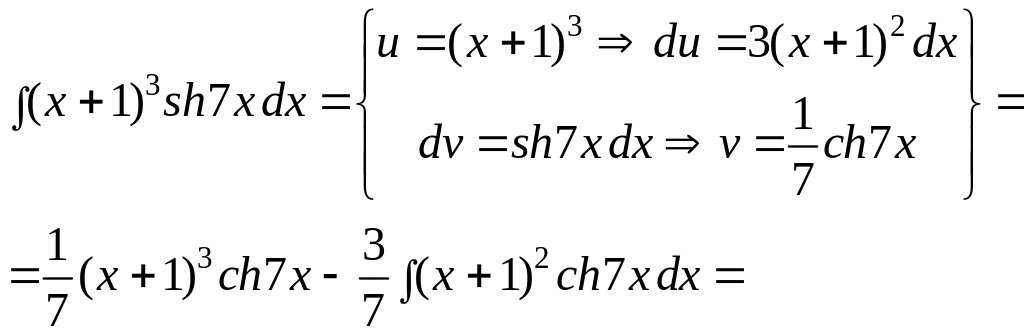
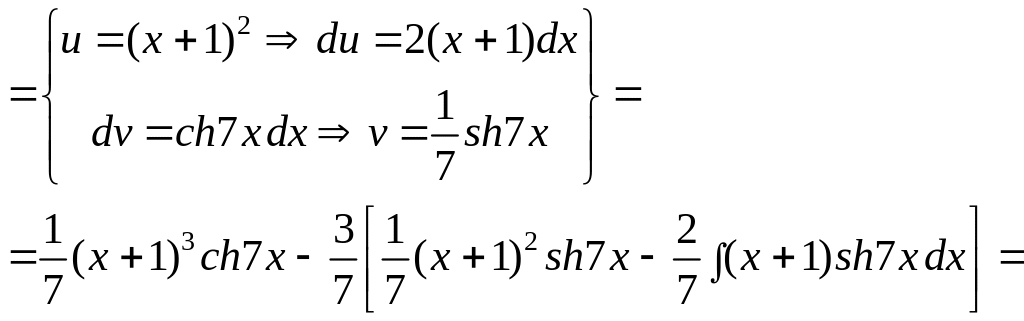
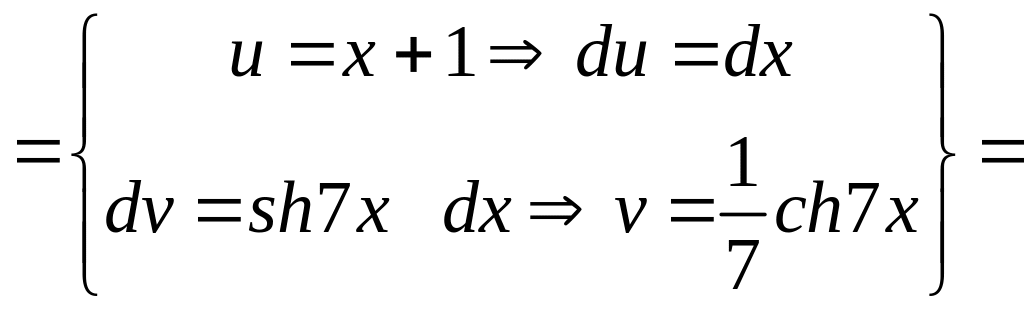
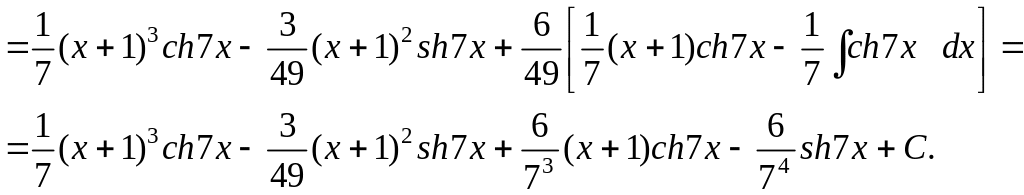
В этой задаче интегрировать по частям пришлось трижды. ▼

Пример 4. Вычислить интеграл

Решение. Конечно, можно получить результат, трижды интегрируя по частям. При этом после первого шага выделится слагаемое с некоторым коэффициентом, после второго шага – слагаемое , затем и, наконец, останется , т.е. в результате получим произведение некоторого многочлена третьей степени на экспоненту :

Из последнего соотношения легко определить коэффициенты Продифференцируем это соотношение:

.

Так как производная от неопределённого интеграла равна подынтегральной функции (одно из основных свойств), то получаем

После сокращения на отличный от нуля множитель и приведения подобных членов получаем равенство

.

Но два многочлена равны тогда и только тогда, когда совпадают коэффициенты при одинаковых степенях. Значит, приходим к системе уравнений

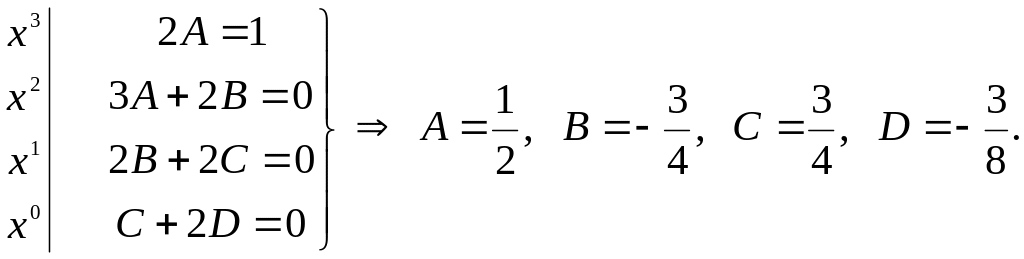
Задача решена:

▼

2. Ко второй группе относятся интегралы от произведения степенной функции на одну из следующих трансцендентных функций:

Здесь в качестве функции , которая далее дифференцируется, следует выбрать трансцендентную функцию. Интегрирование части затруднений не вызовет.

Пример 5. Вычислить интеграл .

Решение. В этой задаче нет вариантов в выборе частей – надо дифференцировать множитель , т.е. , тогда :

▼

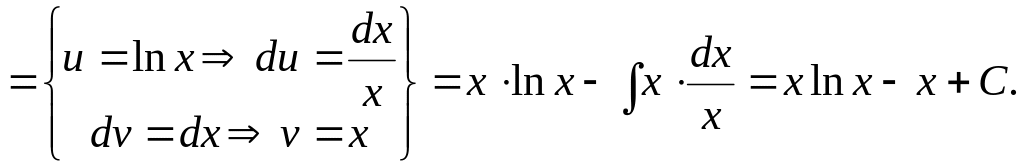Пример 6. Вычислить интеграл .

Решение. В соответствии с рекомендациями дифференцировать следует часть , а интегрировать – часть :

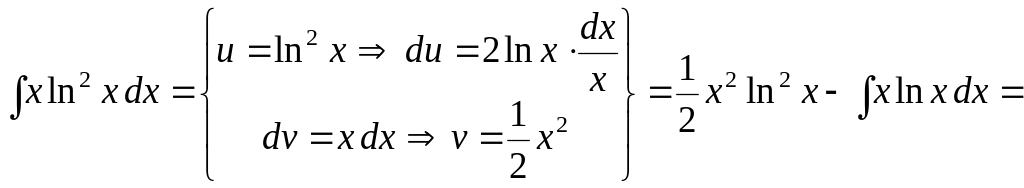
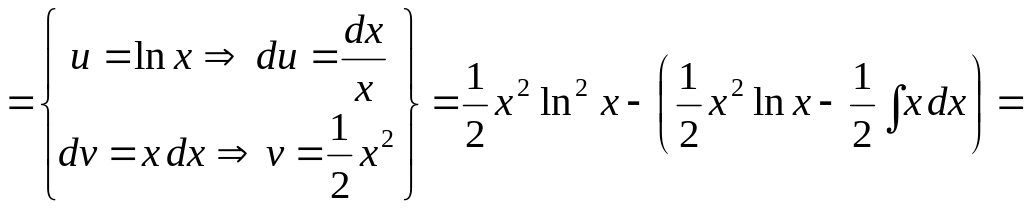
Здесь дважды интегрировали по частям. ▼

Пример 7. Вычислить интеграл .

Решение.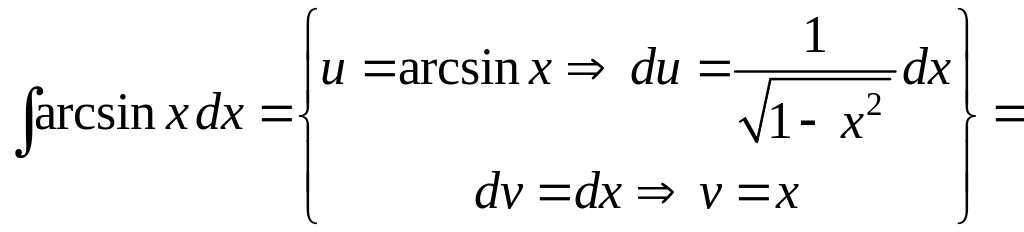

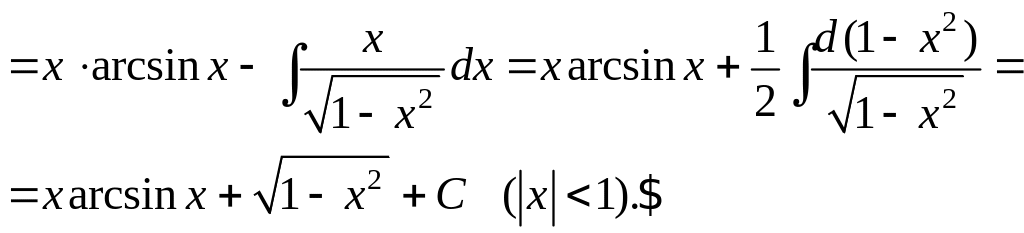
Пример 8. Вычислить интеграл .

Решение.

Здесь для интеграла воспользовались результатом примера 4 из раздела 3. ▼

Пример 9. Вычислить интеграл .

Решение.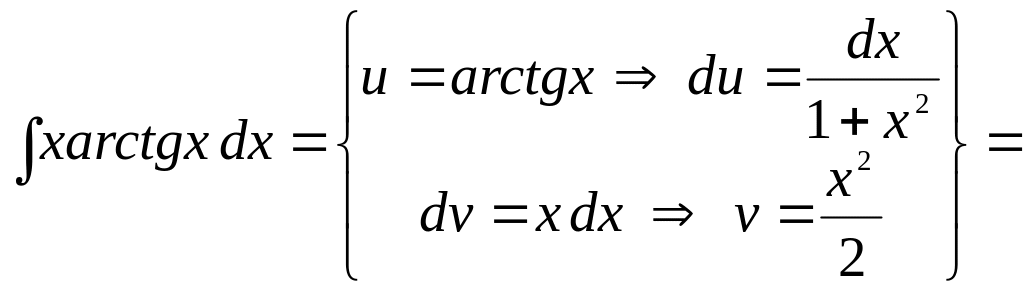

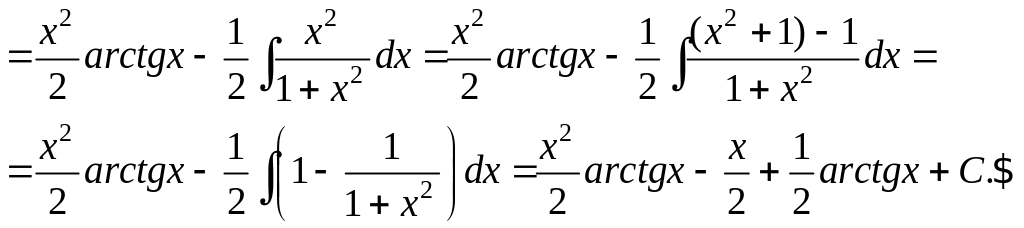
Пример 10. Вычислить интеграл .

Решение. Можно, полагая (а других вариантов здесь нет), интегрировать по частям. Но мы предлагаем сначала сделать замену переменных . Тогда

,

т.е. получили интеграл, вычисленный в предыдущем примере:

.

Осталось вернуться к исходной переменной, заменяя :

= .▼

3. К третьей группе относятся так называемые циклические интегралы. Это прежде всего интегралы вида

Поскольку каждый из множителей в подынтегральной функции одинаково просто и дифференцируется, и интегрируется, части можно выбирать произвольно. При любом выборе частей первый шаг приведет исходный интеграл к интегралу (и наоборот). Еще раз интегрируем по частям, но теперь обязательно надо выбирать части так же, как и первый раз. В результате вновь появится исходный интеграл  цикл завершится. Остаётся решить полученное линейное уравнение относительно .

Пример 11. Вычислить интеграл .

Решение. Начнём с дифференцирования функции и интегрирования функции :

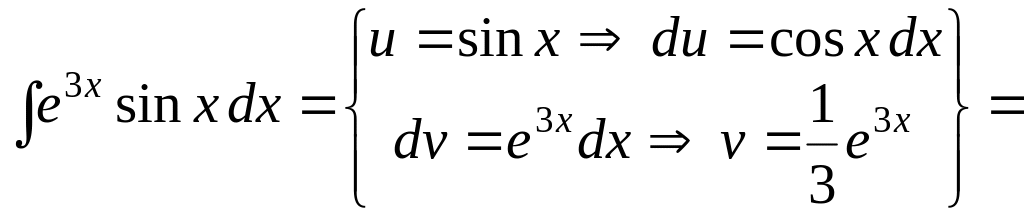
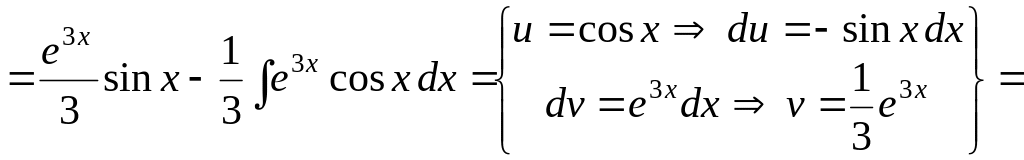
Если обозначим , то можем записать, что

.▼

Пример 12. Вычислить интеграл .

Решение. В этой задаче начнём с дифференцирования функции и интегрирования функции :

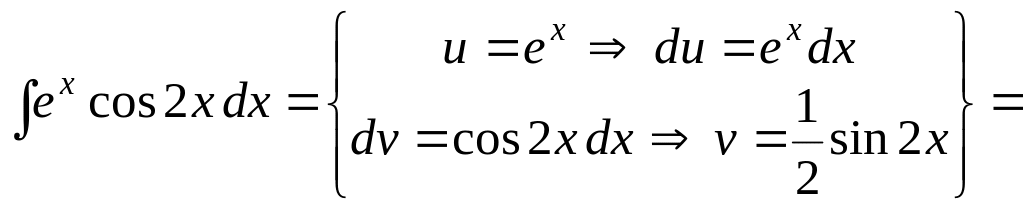
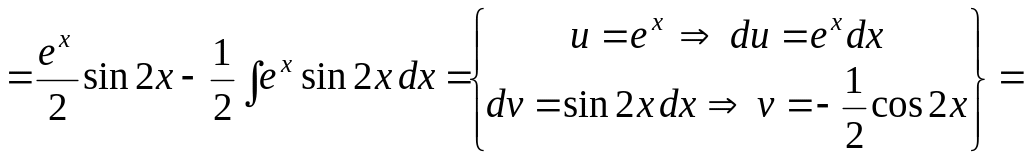
Обозначим , тогда

▼

К циклическим относятся также интегралы

.

Пример 13. Вычислить интеграл .

Решение. Здесь нет вариантов в выборе частей:

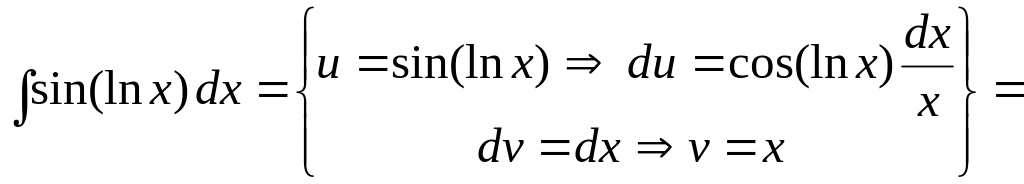
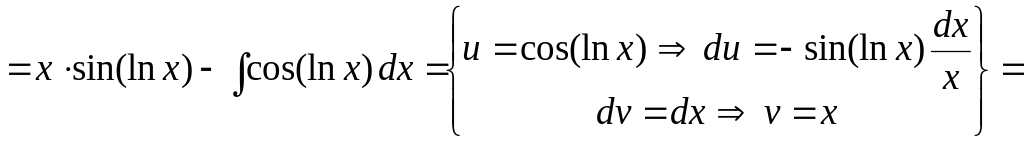
Значит, ▼

Возможности применения метода интегрирования по частям не исчерпываются интегралами из перечисленных групп. Рассмотрим несколько примеров.

Пример 14. Вычислить интеграл .

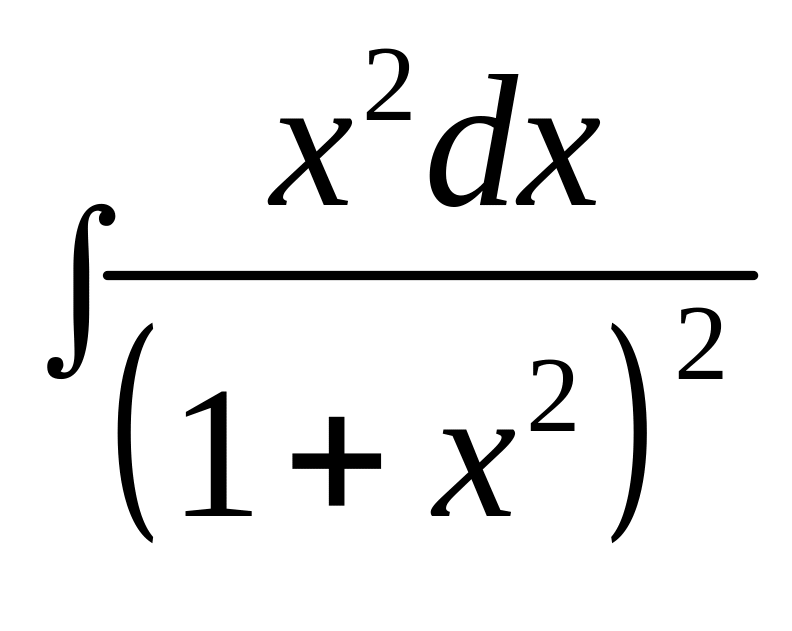Решение. Представим числитель в виде и примем тогда вторая часть – функция легко интегрируется заменой . Получаем

▼

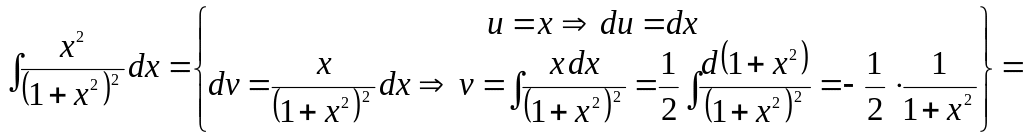
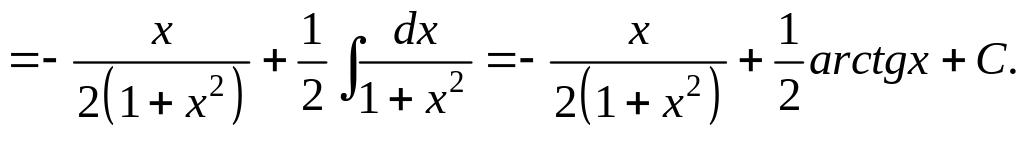Пример 15. Вычислить интеграл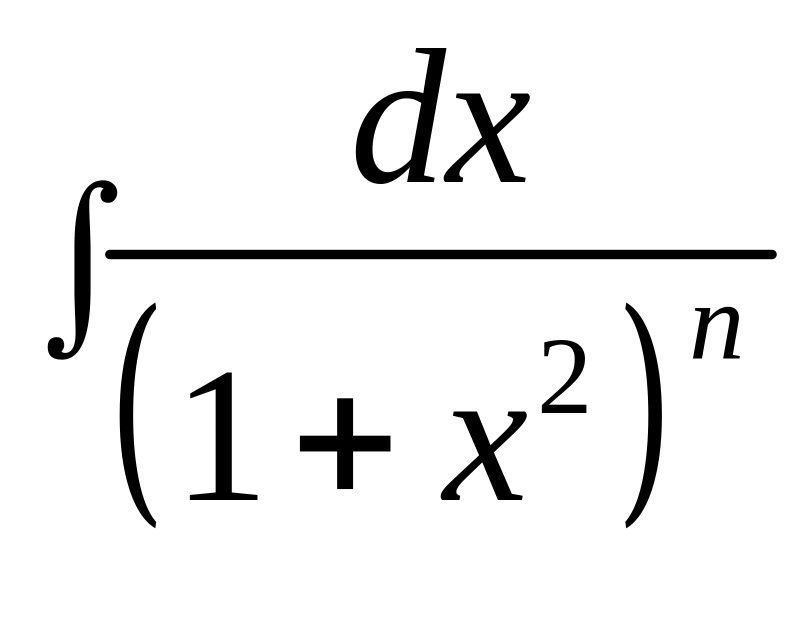 .