Часть 2. Неопределенные интегралы

1. Определение и основные свойства.

Таблица неопределенных интегралов.

Определение. Функция называется первообразной для функции на интервале , если в любой точке она дифференцируема и .

Определение. Совокупность всех первообразных для данной функции на интервале называется неопределенным интегралом от функции и обозначается .

Если - одна из первообразных для функции на , то , где - произвольная постоянная.

Основные свойства неопределенного интеграла

1. , 2.

Свойства 1 и 2 означают, что знаки и взаимно сокращаются, но во втором случае к следует прибавить произвольную постоянную .

3. , 4.

Свойства 3 и 4 называют линейными свойствами интегралов. Из этих свойств следует:

если , то

Таблица простейших интегралов

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11. (в случае знака «минус» )

12.

13.

14.

15.

16.

Основными методами интегрирования являются:

метод преобразования подынтегрального выражения,

метод введения нового аргумента,

метод замены переменной (метод подстановки),

метод интегрирования по частям.

2. Преобразование подынтегрального выражения.

В примерах 1-10 подынтегральное выражение преобразуется так, чтобы в результате получились простейшие табличные интегралы.

Пример 1. Вычислить интеграл .

Решение. (перемножим выражения в скобках, каждый корень представим в виде дробной степени)=

= (воспользуемся линейными свойствами интегралов) = (остается вычислить табличные интегралы )=

.▼

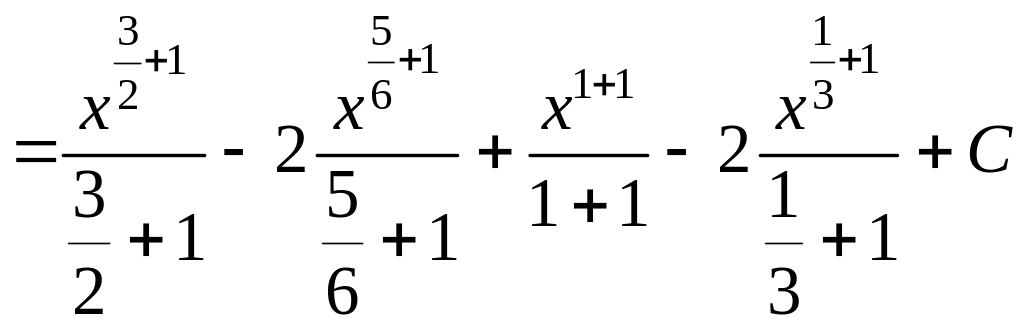
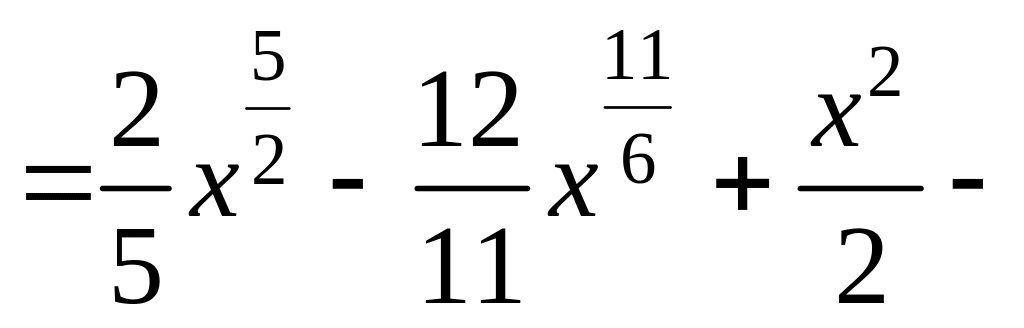
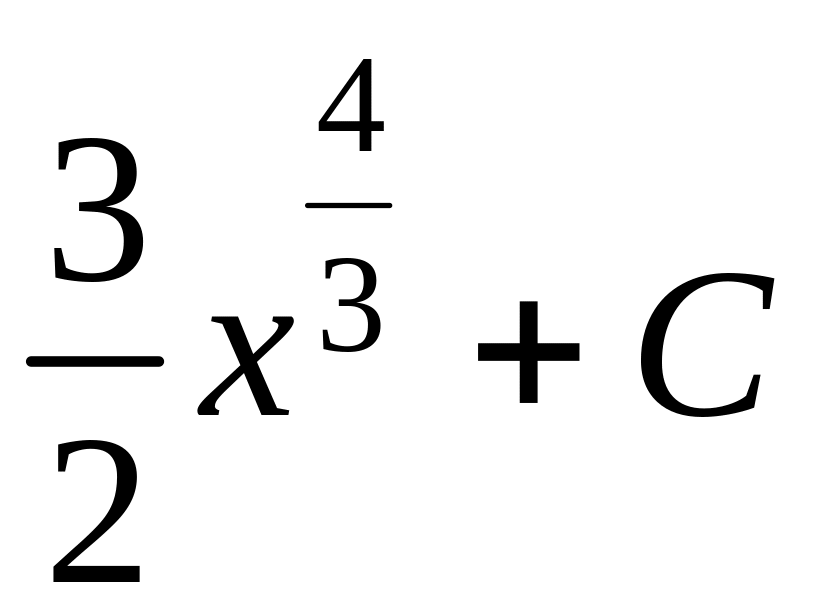
Пример 2. Вычислить интеграл .

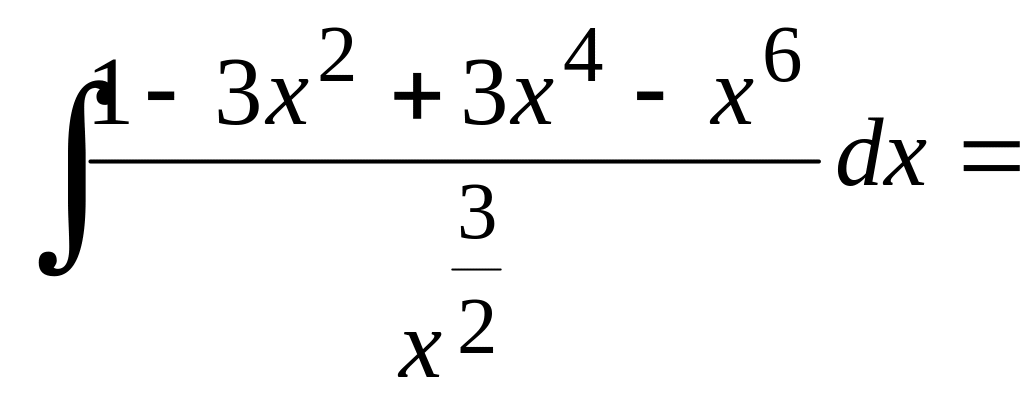Решение. (разность возведем в куб) = = (разделим почленно числитель на )= = (воспользуемся линейными свойствами интегралов)= = = (остается вычислить табличные интегралы )=

.▼

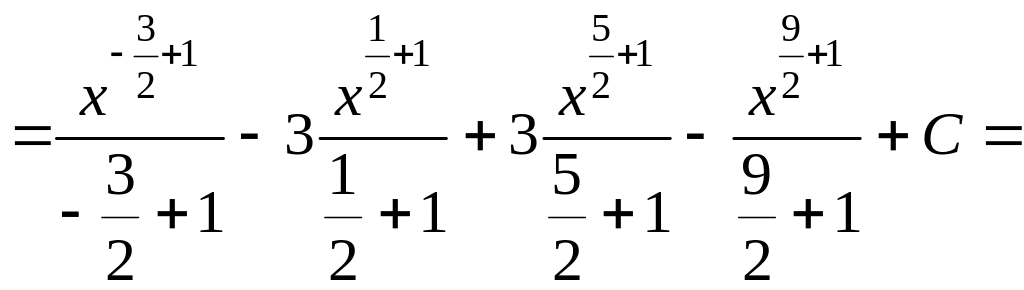
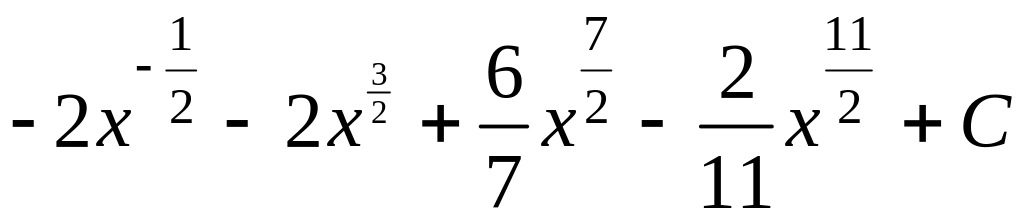Пример 3. Вычислить интеграл .

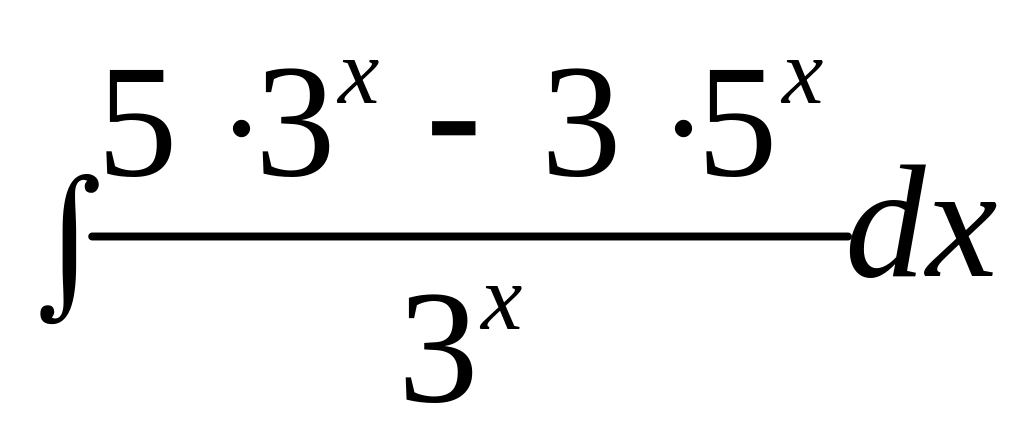Решение.

(делим почленно на ) = (воспользуемся линейными свойствами) = (остается вычислить табличные интегралы и )= .▼

Пример 4. Вычислить интеграл .

Решение.

.

Здесь вспомнили тригонометрические соотношения , и воспользовались линейными свойствами интегралов. ▼

Пример 5. Вычислить интеграл .

Решение.

.

Воспользовались формулой для понижения степени функции и линейными свойствами интегралов. ▼

Пример 6. Вычислить интеграл .

Решение.

.

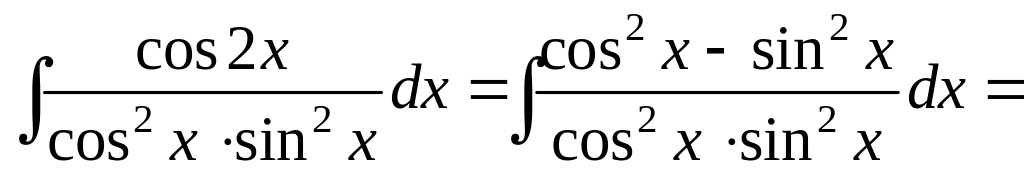
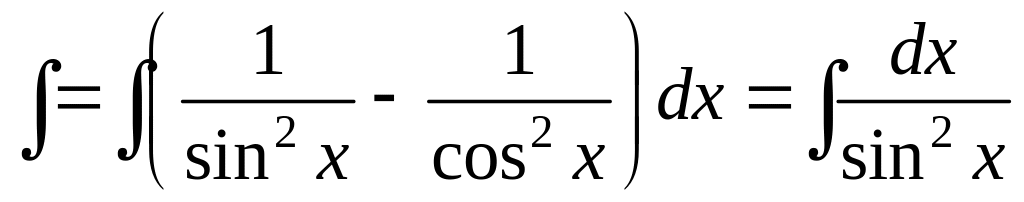
Воспользовались одной из формул для косинуса двойного угла: , затем разделили почленно. ▼

Пример 7. Вычислить интеграл .

Решение. .▼

Пример 8. Вычислить интеграл .

Решение.

.

Здесь подкоренное выражение представили как квадрат суммы

,

затем извлекли квадратный корень (обращаем внимание на то, что ).▼

Пример 9. Вычислить интеграл .

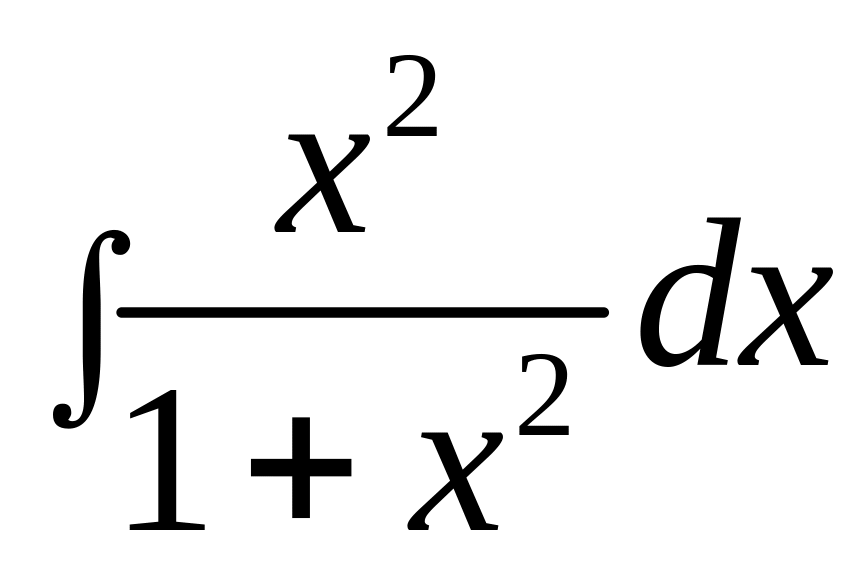Решение.

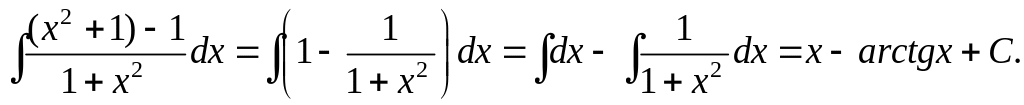
Здесь степень числителя подынтегральной дроби равна степени знаменателя, такая дробь называется неправильной. Неправильную дробь представили в виде суммы целой части и правильной дроби: (выделили целую часть). ▼

Пример 10. Вычислить интеграл .

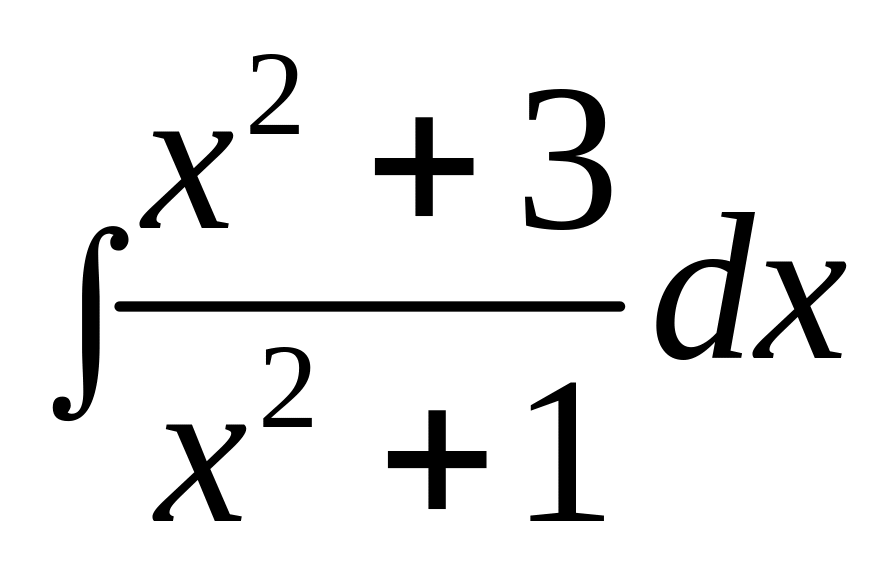Решение.

.

Из неправильной дроби выделили целую часть и воспользовались линейными свойствами интегралов. ▼