Электромагнитные колебания

Мы рассмотрели, какую энергию запасает конденсатор и катушка цепи. Теперь рассмотрим случай, когда в цепи есть и конденсатор и катушка. Такая цепь называется колебательным контуром. Опыт показывает, что в такой цепи возникают электромагнитные колебания. Они могут излучаться или не излучаться в пространство. Почему происходят колебания?

Рис.37

Пусть ключ в положении 1. ( Рис. 37). Конденсатор заряжается от источника до напряжения . Когда конденсатор полностью зарядится, ток прекратится. При этом энергия электрического поля максимальна. Перебросим теперь ключ в положение 2. Емкость начнет разряжаться и в цепи пойдет ток , а любое изменение электрического тока влечет за собой изменение магнитного потока в пространстве. В индуктивности возникает э.д.с. самоиндукции .

Рис.38

В момент времени (точка 1), когда напряжение на конденсаторе станет равным 0, (рис. 38 ), ток максимален. Электрическое поле равно нулю, а магнитное максимально.

От 0 до точки.1 э.д.с. самоиндукции препятствует нарастанию тока в цепи, поэтому он возрастает не мгновенно. Когда ток начинает убывать,э.д.с. теперь препятствует этому уменьшению, ток уменьшается, но идет в том же направлении и перезаряжает конденсатор. В момент времени 2 конденсатор заряжен наоборот (электрическое поле имеет обратный знак). На участке 1-2 ток идет за счет э.д.с. самоиндукции.

– начинает гнать заряды по цепи. Теперь конденсатор опять заряжен – начинается процесс снова. Таким образом, в цепи, содержащей заряженный конденсатор и индуктивность, будет происходить некоторый периодический процесс – переход энергии заряженного конденсатора (энергия электрического поля) в энергию, запасенную катушкой (энергия магнитного поля)

Энергия электрического поля , магнитного

Если считать, что сопротивление в цепи отсутствует (или очень мало), (идеализированный контур), можно записать закон сохранения энергии или

;

Получили дифференциальное уравнение относительно q, т.е. заряда на конденсаторе.

Отсюда:

1. Из вида полученного дифференциального уравнения следует, что q – гармоническая функция времени (cos или sin).

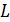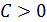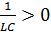2. По самому понятию и , , поэтому можем обозначить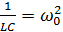

Решением такого уравнения есть гармоническая функция

- собственная частота контура..

Более общая формула: , где – начальная фаза колебания в момент t=0.

Вычислим ток в цепи:

Энергия конденсатора в любой момент времени:

.

Энергия магнитного поля:

1. и больше 0

Рис.39

2. Они находятся в противофазе. (Рис.39).

3. Энергия пропорциональна квадрату амплитуды. .

Свободные затухающие колебания

Во всяком реальном контуре сопротивление не равно нулю. Закон Кирхгофа для цепи, содержащей активное сопротивление:

( )

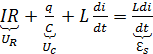Разделим левую и правую часть на :

, обозначим ; .

1. Если 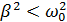, 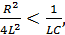решение дифференциального уравнения имеет вид.

где .

частота затухающих колебаний меньше собственных.

График функции имеет вид, показанный на рис.40.

Рис.40

Амплитуда колебаний убывает по экспоненте. Затухание колебаний характеризуют логарифмическим декрементом затухания:

(без вывода)

. Чем больше сопротивление, тем быстрее затухают колебания ( ).

, , , .

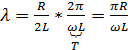- описывается параметрами контура, и – тоже, то есть - это характеристика данного контура. Величина называется добротностью контура.

2. – вместо колебаний происходит апериодический разряд конденсатора. (Вся энергия сразу теряется на активном сопротивлении). Колебаний нет.

Когда , ( , отсюда:

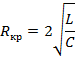Это сопротивление называется критическим.