Инженерные правила.

1. Правило левой руки.

Его применяют для определения направления силы, действующей на проводник с током в магнитном поле.(рис. 10)

Рис.10.

Левую руку располагают так, что бы магнитные силовые линии входили в ладонь, а 4 вытянутых пальцев показывают направление тока, отставленный большой палец указывает направление силы.

2. Правило буравчика

Правило основано на уравнении Био-Савара-Лапласса. Позволяет определить направление магнитных силовых линий, (вектор магнитной индукции в любой точке касателен к магнитным силовым линиям)

А) Определение направления индукции прямого тока.

Поступательное движение буравчика направлено по направлению тока, тогда вращение головки показывает направление магнитных силовых линий. (рис.11)

Рис.11.

Б) Определение индукции кругового тока.

Вращательное движение буравчика - по направлению тока, индукция - вдоль

поступательного движения буравчика.(рис.12)

Рис.12.

ЛЕКЦИЯ 3

Теорема о циркуляции вектора индукции магнитного поля.

Дифференциальные уравнения магнитного поля.

Закон полного тока.

Для электрического поля получали формулу:

(1) , или то же самое:

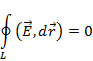
(работа сил электрического поля по замкнутому контуру равна нулю). Таким образом, доказывали, что электрическое поле – это поле консервативных сил, то есть, оно потенциально, из (1): . Вывод: электростатическое поле – безвихревое.

Наша задача: вычислить, чему равен , посмотреть, потенциально ли магнитное поле. Если , то поле потенциально, если нет, то . – это не проводник с током, а просто любой контур в магнитном поле с индукцией . В общем случае эта задача очень сложная, поэтому рассмотрим частный случай.

Мы уже находили, что магнитная индукция кругового тока равна:

Выберем контур по силовой линии (окружность с радиусом ).Вектор перпендикулярен вектору .

= =

Для контура диаметром получим то же самое: . Можно показать, что этот результат справедлив для контура любой формы и не обязательно плоского, таким образом , то есть магнитное поле не потенциально. Оно вихревое, так как .

Если контур охватывает несколько токов, то:

Токи, входящие в контур, беруться со знаком +, токи, выходящие из контура, со знаком -

Рис. 15

(Это не обязательно все проводники с током, это может быть, например, поток электронов в осциллографе). Если контур токов не охватывает, то . Чтобы учесть все токи, проводят построение: строят произвольную поверхность, S, опирающуюся на контур Рис.16.

Рис. 16

–плотность тока в каждой точке поверхности S.

отсюда:

– магнитное поле имеет вихревой характер. Последние уравнение называется дифференциальной формой закона полного тока. Вспомним, что 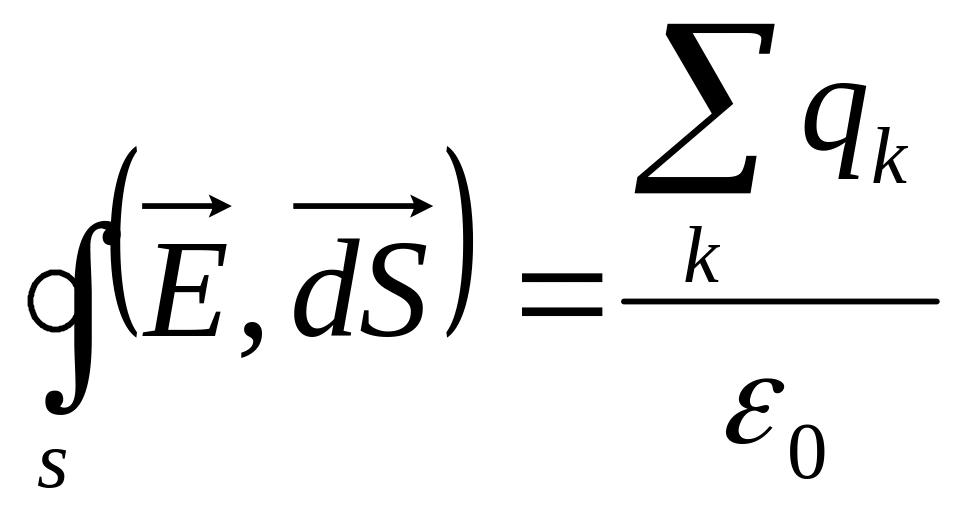, откуда получапи: (источник электростатического поля). В природе магнитных зарядов не существует, поэтому поток вектора через замкнутую поверхность равен нулю.

,

Пример применения теоремы о циркуляции вектора магнитной индукции.Магнитное поле длинного соленоида.

Соленоид – это катушка без сердечника. Магнитные силовые линии вокруг одного витка имеет вид:

Рис. 17

В соленоиде магнитные силовые линии проходят следующим образом: (Рис.18)

Рис. 18

Внутри катушки – однородное магнитное поле. Вектор в любой точке параллелен оси соленоида.

Рис. 19

Выберем контур 1234. (рис.). Участок 34 лежит на оси соленоида. Запишем теорему о циркуляции вектора магнитной индукции:

Участок 4,1:

1,2:

2,3: =0

3,4 =

Так как контур токов не охватывает, . Мы выбирали контур произвольно, поэтому в любой точке внутри соленоида магнитная индукция равна магнитной индукции на оси. Теперь выберем контур следующим образом: (Рис.20)

Рис. 20

На участках 1,4 и 2,3: :

n – число витков на единицу длины соленоида. na – число витков на длине a.

Докажем, что = 0. Возьмем плоскость перпендикулярную оси соленоида. Магнитные силовые линии всегда замкнуты. Магнитный поток . В силу замкнутости магнитных силовых линий - поток внутри соленоида равен потоку вне соленоида. , так как внешняя площадь стремится к бесконечности, должно стремится к 0, то есть так как – конечно.

Рис.21

Таким образом, для соленоида:

Величина nI имеет размерность: .

ЛЕКЦИЯ 4

Рамка с током в магнитном поле. Магнитный момент.

Рассмотрим плоский контур в однородном магнитном поле. В принципе любой неплоский контур можно разбить на плоские контуры. Найдем направление сил, действующих на каждую из сторон рамки:

(используя правило левой руки или правило перемножения векторов)

Рис. 22 Рис. 23

Составляющие 1 и 2 будут вызывать вращение рамки. – нормаль к плоскости рамки. Вращающий момент будет стремиться повернуть рамку перпендикулярно магнитным силовым линиям. Если она так остановится, то далее вращаться не будет.

Найдем величину этого вращающего магнитного момента. Составляющие и растягивают рамку, а и - вращают ее.

(в нашем случае)

Момент пары сил:

По правилам механики момент силы направлен по оси вращения (в данном случае - вверх). Последнее равенство можно переписать в виде векторного произведения, если обозначить

Величина называется магнитным моментом рамки с током, то есть, на рамку (контур) с током в магнитном поле действует вращающей механический момент, зависящий от величины тока I , площади рамки, ориентации рамки и от величины магнитного поля . Таким образом, магнитное поле стремится установить рамку с током перпендикулярно магнитным силовым линиям, то есть так, чтобы вектор был направлен вдоль магнитных силовых линий.