2.2 Математичний апарат мгб

У процесі складання МГБ розраховують коефіцієнти прямих матеріальних витрат , тобто відношення обсягу продукції i -ї галузі, яку викори-стовують в j – й галузі, до загального обсягу валової продукції j – ї галузі-споживача:

= (i, j = 1, n) (2.3).

Цей коефіцієнт показує, яку кількість продукції у вартісному виді i -ї галузі треба витрати на виробництво одиниці валової продукції j – ї галузі.

Підставивши (2.3) в (2.1), одержимо:

X = (i= 1, n ). (2.4)

Або маємо:

X =

X = (2.5)

………………………………………

X =

Рівняння (2.4) або (2.5) називають системою рівнянь статичного міжгалузевого балансу, або економіко-математичною моделлю міжгалузевого балансу виробництва і розподілу продукції. Модель МГБ відображає економічні і технологічні зв’язки між галузями-виробниками і галузями-споживачами. Технологічні зв’язки вимірюють за допомогою коефіцієнтів прямих матеріальних витрат, які виражають кількість продукції галузі-виробника, яку споживають під час виробництва одиниці валової продукції галузі-споживача. Для балансу у натуральному вираженні вони характеризують норму витрат продукції i -ї галузі на виробцтво одиниці валової продукції j – ї галузі. Тому коефіцієнти прямих витрат не можуть бути вищими за 1.

Як правило, коефіцієнти прямих витрат визначають на рівні середніх величин для відповідних галузей. Коефіцієнти вважають незмінними або пе-реглядають їх при розробці планових (перспективних) балансів.

Рівняння (2.5) можна записати у матричній формі:

X = A X + Y (2.6),

X = B Y (2.7),

де А – матриця коефіцієнтів прямих витрат,

B – матриця коефіцієнтів повних витрат.

В розгорнутому вигляді рівняння (2.7) запишеться так:

X = b b ... b

X = b b …b

…. …………… … (2.8)

X = b b …b

Матрицю В обчислюють за формулою

B = (E – A) (2 .9),

тобто знаходять шляхом обернення матриці (Е – А). Тут Е – одинична матриця.

Коефіцієнт повних витрат показує кількість валової продукції галузі-виробника, яку споживають під час виробництва одиниці кінцевої продукції галузі-споживача. Коефіцієнти перевищують коефіцієнти , тому що вони враховують не тільки прямі, а й непрямі витрати, які мали місце на попе-

редніх етапах виробництва.

Можна також знайти коефіцієнти прямих витрат праці

, j = 1, n (2.10),

коефіцієнти прямих витрат основних фондів

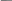
, j = 1, n (2.11).

За їх допомогою у плановому МГБ можна визначити потребу відповідно у трудових ресурсах і основних фондах для сфери матеріального виробництва.