Appendix 1.1. Wave fronts approximation

Let us consider some complex amplitude

(1.181)

o

Figure 1.92

f the freely propagating wave, cf. Figure 1.92, the amplitude of which, , changes slowly, so that the wave is modulated in phase alone. Further propagation of the wave results not only in distortion of a wave front, but also in changing the amplitude. So, the wave at some distance from the plane , at the plane , is modulated both in phase and in intensity. However, if the phase modulation obeys some specific conditions, then the wave propagation from one plane to another is almost diffractionless. This process can be algorithmized using the proper approximation techniques, for example the stationary phase method [28,54].

The field at the plane is connected with the field at the plane by the Fresnel transform:

. (1.182)

In correspondence of the stationary phase method, if the amplitude specified in is the function with a sharp spectrum, and the phase  changes slowly enough, then Eq. (А2.2) can be considerably simplified.

Two-dimensional interpretation of the stationary phase method is of the form:

 , (1.183)

where is the doubly differentiated in function, belong to being the solutions of the equations:

. (1.184)

For that, the point is the single point of this kind in , and are the partial derivatives at the point , and the following conditions are fulfilled for the second derivatives:

. (1.185)

In our case,

= . (1.186)

It follows from Eq. (1.185) that must be the function doubly differentiated in . Eqs. (1.184) are transformed to the form:

, (1.187)

and Eqs. (1.185) are transformed to the form:

, (1.188)

where are the solutions of Eqs. (1.187). Thus, the field at the plane can be represented in the form:

. (1.189)

If such point is not the single one in , then the field is determined as the sum of the fields of the form (1.189) corresponding the each solution. In the case of infinitely large set of the solutions of Eqs. (1.187), i.e. if at least one of the solutions degenerates to uncertainty, then the field corresponding to this uncertainty degenerates to delta-function. Physically, such situation corresponds to the formation of caustics or to the point of focusing of a spherical wave.

We will refer to Eq. (1.189) as the wave fronts approximation.

One-dimensional interpretation of the wave fronts approximation is of the form:

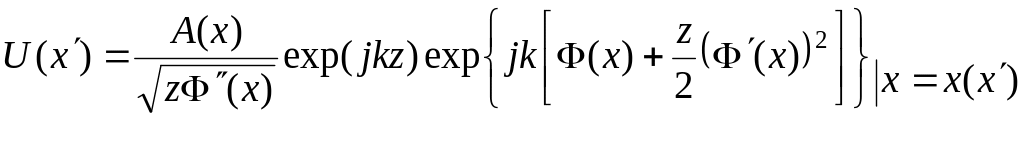, (1.190)

where are the first and the second derivatives from the phase modulation, and is the solution of the equation:

. (1.191)

For that, the following condition must be fulfilled:

. (1.192)

Let us analyze the requirements to the wave, which provide applicability of this approximation to describing its propagation. For the sake of simplicity, we analyze a one-dimensional case. Let us decompose into series on the degrees of in the vicinity of the point x_0, which is the solution of Eq. (1.191). Then, accounting that , Eq. (1.182) takes the form:

. (1.193)

The integral in Eq. (1.193) can be interpreted as some field formed by the transparent with transmittance illuminated by the plane wave at the distance from the plane . For description of the field at the plane by Eq. (1.190), i.e. to be proportional to , it is necessary that the approximation similar to the “shadow approximation” [40] be valid for Eq. (1.193).

Let us do the following substitution:

. (1.194)

Correspondingly, the complex amplitude can be described by the following equation:

. (1.195)

Let us introduce for the angular spectrum:

. (1.196)

It can be shown that

. (1.197)

Obviously, if is slightly different from unity within some vicinity ( ), and is the function with a large spectrum (i.e. decreases rapidly for no belonging to this vicinity), then Eq. (1.197) is transformed into Eq. (1.190). In other words, , if ®1, where is some limiting frequency, beginning from which the contribution of the angular spectrum components in the resulting field can be neglected.

For the rectangular aperture with a side 2a such limiting frequency is often determined as and corresponds to the first minimum of the angular spectrum. Besides, about 90% of energy of radiation passing the aperture is concentrated at the central maximum. By analogy with an aperture, we will believe that the limiting frequencies are the ones limiting the spectral domain bearing 90% of energy associated with . Thus, satisfies the condition:

. (1.198)

In agreement with the Rayleigh criterium, , if .

Thus, the condition (1.198) and the relation

(1.199)

form the criterium of validity of the wave fronts approximation.

Appendix 1.2. Fourier image of isotropic vortex

The phase part of the complex amplitude of the isotropic vortex, , written in polar coordinates with the origin at the center of a vortex, is , and the modulus of such complex amplitude, , is represented as the product:

, (1.200)

where is the pupil function limiting the isotropic vortex.

Let us find out the Fourier image of the isotropic vortex,

, (1.201)

where are the polar coordinates at the frequency domain. The double integral is transformed to the following one:

. (1.202)

The inner integral, hereinafter referred to as , is reduced to the following relation:

, (1.203)

where is the Bessel function of the -th order. Using the well-known relation [105]:

, (1.204)

and taking into account that only the singly charged vortices exist in reality ( ), one can reduce Eq. (1.203) to the form:

. (1.205)

Following,

. (1.206)

Substituting and taking into account that [106]:

, (1.207)

one obtains the following relation for :

. (1.208)

It cab be shown that .

Thus, the vortex function is the Fourier image of an isotropic vortex. Within the vortex core (for small ), where the following relation is valid [85]:

. (1.209)

has the form:

. (1.210)

In other words, isotropic vortex does not change its structure into frequency domain.

Appendix 1.3. Poynting vector. paraxial approximation

Let us make the following assumptions: (i) the fields of interest are completely coherent; (ii) the wave propagates in a free space, and the paraxial approximation is valid.

Let be the vectors of strength of the magnetic and electrical fields, respectively. The components of these vectors are conventionally determined, cf. Ref. 28, as

etc., (1.211)

where ( , ) are the amplitudes and the spatial phases of the corresponding components. The quantities … etc. are, in general, the functions of all three coordinates.

Under paraxial approximation, the scalar product tends to , excluding some peculiar situations, as the field in the vicinity of the vortex core. Then, Eq. (1.211) is transformed to the form:

etc. (1.212)

Let be the complex wave functions of the magnetic and the electrical fields, respectively. The components of these vectors are determined in the following manner. For example:

, (1.213)

where .

It is known [3] that

, (1.214)

where is the wave number.

Thus, knowing , one can represent the complex wave function of the magnetic field, , through the complex wave function of the electrical field.

Further, using the standard relations for the complex amplitudes, one can compute the averaged in time magnitude of the Poynting vector or the averaged orbital momentum of the electromagnetic field [95].

Here, we preserve the temporal dependence and obtain the relations describing the instantaneous components of the Poynting vector. We explore the field strengths.

Here, we preserve the temporal dependence and obtain the relations describing the instantaneous components of the Poynting vector. We explore the field strengths.

Using Eq. (1.214) and the fact that , one can find that

, (1.215)

where , is the shifted in phase by strength of the electrical field . Bearing in the mind the further transition to the components of the electrical field alone, hereinafter we designate the quantities as .

As it is known [28], the Poynting vector is represented by the relation:

, (1.216)

or, in components, by the relations:

. (1.217)

Using Eqs. (1.215-1.217) and excluding all derivatives on and derivatives on -component due to their negligible magnitudes (excluding the terms containing large factor ), one obtains the following equations for the components of vector :

, (1.218)

where , and .

Let us represent in terms of . To do this, we use the equation, which is valid for a freely propagating wave, written for the complex amplitude of the electrical field:

, or , (1.219)

where is the transversal component of vector .

Besides, we take into account that under paraxial approximation all terms containing the derivatives on are small, excluding the terms containing as the factor. In this case, the following relation is valid [100]:

. (1.220)

It follows from Eqs. (1.219) and (1.220) that

. (1.221)

One obtains from Eq. (1.221):

, (1.222)

where .

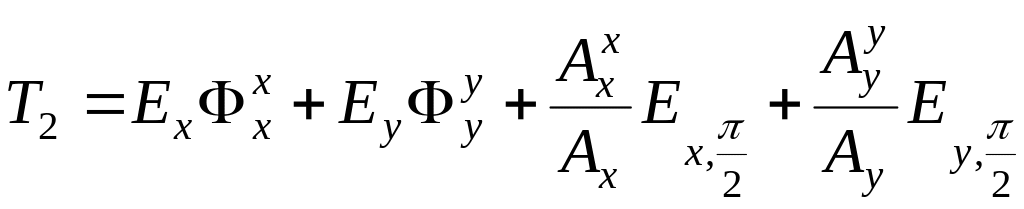Then, accounting Eq. (1.222) Eqs. (1.218) is rewritten in the form:

, (1.223)

where

. (1.224)

Thus, under paraxial approximation, the relations for the instantaneous components of the Poynting vector can be described in terms of the characteristics of the - and the -components of electrical field alone.

The modulus of the transversal component of the Poynting vector is written as:

. (1.225)

The orientation of the transversal component is determined by the ratio . Thus, the direction of the Poynting vector’s component at the -plane is determined as :

. (1.226)

References for chapter 1

1. M. Fracon, La Granularite Laser (Spekle) et ses Applications en Optique, Masson, Paris New York Barcelone Milan, (1978).

2. J.W. Goodman, Statistical Optics, A.Wiley Interscience Publication, John Wiley and Sons, New York, Chichester, Brisbane, Toronto, Singapore, (1985).

3. J.F. Nye, Natural Focusing and Fine Structure of Llight, Institute of physics publishing, Bristol and Philadelphia, 1999.

4. J.F. Nye, M. Berry, “Dislocations in wave trains”, Proc. R. Soc. Lond., Vol. A 336, pp. 165-190, (1974).

5. M.V. Berry, “Singularities in waves and rays”, Physics of defects. Les Houches Session XXXV, 28 July - 29, August 1980, Amsterdam: North-Holland., pp. 453-543, (1981).

6. Reference List on Singular Optics, G. Swartzlander, Jr., http://www.u.arizona.edu/~grovers/SO/.

7. J.F. Nye, “The Motion and structure of dislocations in wave fronts” Proc. R. Soc. Lond., Vol. A 378, pp. 219-239, (1981).

8. N.B. Baranova, B.Ya. Zeldovich, “Wavefront dislocations and amplitude zeroes”, JETP, Vol. 80, № 5, pp. 1789-1797, (1981).

9. N.B. Baranova, B.Ya. Zeldovich, A.V. Mamayev, N.F. Pilipetsky, V.V. Shkunov, “Investigation of wavefront dislocations density in the light field”, JETP, Vol. 83, № 5, pp. 1702-1710, (1982).

10. N.B. Baranova, A.V. Mamayev, N.F. Pilipetsky, V.V. Shkunov, B.Ya. Zeldovich, “Wavefront dislocations: topological limitations for adaptive systems with phase conjugation”, J. Opt. Soc. Am A, Vol. 73, pp. 525-528, (1983).

11. J.F. Nye, J.V. Hajnal, J.H. Hannay, “Phase saddles and dislocations in two-dimensional waves such as the tides”, Proc. R. Soc. Lond., Vol. A 417, pp. 7-20, (1988).

12. I. Freund, N. Shvartsman, V. Freilikher, “Optical dislocation networks in highly random media”, Opt. Comm., Vol. 101, pp. 247-264, (1993).

13. I. Freund, N. Shvartsman, “Wave-field singularities: The sign principle”, Phys. Rev. Vol. 50 (6), pp. 5164-5172, (1994).

14. “Optical Vortices”, Horizons in world physics, Vol. 228, Edited by M. Vasnetsov, K. Stliunas, Nova Science Publ., (1999).

15. M.V. Berry, J.F. Nye, F.J. Wright, “The elliptic umbilic diffraction catastrophe”, Proc. R. Soc. Lond. Vol. A 291, pp. 453-484 (1979).

16. M. Vaupel, C.O. Weiss, “Circling optical vortices”, Phys. Rev. A, Vol. 51, pp. 4078-4085, (1995).

17. I. Freund, “Saddles, singularities, and extrema in a random-phase fields”, Phys. Rev. E, Vol. 52, pp. 2348-2360, (1995).

18. N. Shvartsman, I. Freund, “Speckle spots ride phase saddles sidesaddle”, Opt. Comm., Vol. 117, pp. 228-234, (1995).

19. I. Freund, “Critical-point level-crossing geometry in wave fields”, J. Opt. Soc. Am. A, Vol. 14, pp. 1911-1927, (1997).

20. I. Freund, “‘1001’ correlations in random wave fields”, Waves Random Media, Vol. 8, pp. 119-158, (1998).

21. I. Freund, N. Shvartsman, “Vortices in Random Wave Fields: Nearest Neibor Anticorrelations”, Physical Review Letters, Vol. 72, pp. 1008-1011, (1994).

22. I. Freund, “Amplitude topological singularities in random electromagnetic wavefields” Phys. Lett. A. Vol. 198, pp.139-144, (1995).

23. I. Freund, “Vortex derivatives”, Opt. Comm., Vol. 137, pp. 118-126, (1997).

24. I. Freund, “Optical phase maps”, SPIE Proc., Vol. 2389, pp. 411-419, (1995).

25. I. Mokhun, “Amplitude zeroes and structure of statistical optical fields. Correlation between the field’s intensity and phase”, Proc. SPIE, Vol. 3573, pp. 567-571, (1998).

26. O.V. Angelsky, R.N. Besaha, O.V. Kovalchuk, I.I. Mokhun, “Structure of statistical scalar fields”, Nauk. Visn. Cherniv. Univ., Vol. 66, Physics, Electronics, pp. 66-68, (1999).

27. I. Freund, V. Freilikher, “Parameterization of anisotropic vortices”, JOSA A, Vol. 14, 1902-1910, (1997).

28. M. Born, E. Wolf, “Principles of Optics”, 6^th (corrected) ed. (Pergamon Press, Oxford: 1987).

29. G. Indebetouw, “Optical vortices and their propagation”, J. of Mod. Opt., Vol. 40, pp. 73-87, (1999).

30. N.R. Heckenberg, R. McDuff, C.P. Smith, H. Rubinsztein-Dunlop, M.J. Wegener, “Laser beams with phase singularities”, Opt. & Quant. Electr., Vol. 24, pp. S951-S962, (1992).

31. N.R. Heckenberg, M. Vaupel, J.T. Malos, C.O. Weiss, “Optical-vortex pair creation and annihilation and helical astigmatism of a nonplanar ring resonator”, Phys. Rev. A, Vol. 54, pp. 2369-2378, (1996).

32. M.V. Berry, “Much ado about nothing: optical dislocation lines (phase singularities, zeroes, vortices…)”, Proc. SPIE., Vol. 3487, pp. 1-5, (1998).

33. M.V. Berry, “Wave dislocation reactions in non-paraxial Gaussian beams”, J. Mod. Opt., Vol. 45, pp. 1845-1858 (1998).

34. E. Abramochkin, V. Volostnikov, “Spiral-beams: optical and quantum aspects” Opt. Comm., Vol. 125, pp. 302-323, (1996).

35. E.V. Abramochkin, Volostnikov, “Structurally stable singular wavefields”, Proc. SPIE, Vol. 3487, pp. 20-28, (1998).

36. A.G. White, C.P. Smith, N.R. Heckenberg, H. Rubinsztein-Dunlop, R. McDuff, C.O. Weiss, “Interferometric measurements of phase singularities in the output of a visible laser”, J. Mod. Opt., Vol. 38, pp. 2531-2541, (1991).

37. I.V. Basisty, M.S. Soskin, M.V. Vasnetsov, “Optical wavefront dislocations and their properties”, Opt. Comm., Vol. 119, pp. 604-612, (1995).

38. M.S. Soskin, M.V. Vasnetsov, I.V. Basisty, “Optical wavefront dislocations”, Proc. SPIE, Vol. 2647, pp. 57-62, (1995).

39. N.R. Heckenberg, R. McDuff, C.P. Smith, A.G. White, “Generation of optical singularities by computer-generated holograms”, Opt. Lett., Vol. 17, pp. 221-223, (1992).

40. S.M. Rytov, Yu.A. Kravtsov, and V.I. Tatarsky, Principles of Statistical Radiophysics, Springer, Berlin, (1989).

41. I. Freund, “Optical vortex trajectories”, Opt. Comm., Vol. 181 pp. 19-33, (2000).

42. D. Rozas, C.T. Law, G.A. Swartzlander, “Propagation dynamics of optical vortices”, JOSA B, Vol. 14, pp. 3054-3065, (1997).

43. D. Rozas, Z.S. Sacks, G.A. Swartzlander, “Experimental observation of fluidlike motion of optical vortices” Phys. Rev. Lett., Vol. 79 pp. 3399-3402, (1997).

44. N.N. Rozanov, “Radiation formation with wavefront dislocations”, Opt. and Spectroscopy, Vol. 75, pp. 861-867, (1993).

45. K.W. Nicholls, J.F. Nye, “Three-beam model for studying dislocations in wave pulses”, Journ. of Phys. A Mathem. & General, Vol. 20, pp. 4673-4696, (1987).

46. J. Masajada, B. Dubik, “Optical vortex generation by three plane wave interference”, Opt. Comm., Vol. 198 pp. 21-27, (2001).

47. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, “Appearance of wave front dislocations under interference among beams with simple wave fronts”, Optica Aplicata, Vol. XXVII, №4, pp. 273-278, (1997).

48. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, “Appearance of wave front dislocations under interference among beams with simple wave fronts”, SPIE Proc., Vol. 3317, pp. 97-100, (1997).

49. J.F. Nye, “Unfolding of higher-order wave dislocations”, J .Opt .Soc. Am. A, Vol. 15, pp. 1132-1138, (1998).

50. G.P. Karman, A. van Duijl, J.P. Woerdman, “Unfolding of an unstable singularity into a ring”, Opt. Lett., Vol. 23, pp. 403-405, (1998).

51. G.P. Karman, J.P. Woerdman, “How phase and amplitude aberration destabilized the phase singularities”, J. Opt .Soc. Am. A, Vol. 15, pp. 2862-2868, (1998).

52. V.P. Lukin, V.A. Sennikov, V.A. Tartakovski, “Optical vortices: creation, annihilation, and modeling”, Proc. SPIE, Vol. 4724, pp. 85-93, (2002).

53. O.V. Angelsky, R.N. Besaha, O.V. Konovchuk, I.I. Mokhun, “Generation of vortex beams”, Nauk. Visn. Cherniv. Univ., Vol. 79, Physics, Electronics, pp. 40-42, (2000).

54. L. Mandel, E. Wolf, Optical coherence and quantum optics, Cambridge university press, (1995).

55. F.T. Arecchi, G. Giacomelli, P.L. Ramazza, S..Residori, “Vortices and defect statistics in two-dimensional optical chaos” Phys. Rev. Lett. Vol. 67, 3749-3752б (1991).

56. V.A. Zuravlev, I.K. Kobozev, Yu.A. Kravtsov, “Statistical characteristics of phase front dislocations of a wave field”, JETP, Vol. 75, pp. 256-262, (1992).

57. I. Freund, “Optical vortices in Gaussian random wave fields: statistical probability densities”, JOSA A, Vol. 11 pp. 1644-1652, (1994).

58. T.I. Arsenyan, S. Embaukhov, N. Fedotov, P. Korolenko, G. Petrova, “Statistical characteristics of light fields with helical dislocations of the wave front”, Proc. SPIE, Vol. 3487, pp. 148-155, (1998).

59. J. Max, “Methodes et Techniques de Traitement du Signal et Applications aux Measures Physiques”, Part 1, Masson, Paris New York Barcelone Milan Mexico Rio de Janeiro, (1981).

60. O. Angelsky, R. Brandel, I. Mokhun, “Characteristics of scalar random field and its vortex networks. Recovery of the optical phase”, SPIE Proc., Vol. 4607, pp. 25-29, (2002).

61. H.P. Baltes, “Inverse Source Problems in Optics”, Springer – Verlag, Berlin, (1978).

62. J.F. Nye, “Line singularities in wave fields”, Phil. Trans. R. Soc. Lond. Vol. A 355, pp. 2065-2069, (1997).

63. J.F. Nye, “Polarization effects in the diffraction of electromagnetic waves: the role of disclinations”, Proc. R. Soc. Lond., Vol. A 387, pp. 105-132, (1983).

64. J.F. Nye, “Lines of circular polarization in electromagnetic wave fields”, Proc. R. Soc. Lond., Vol. A 389, pp. 279-290, (1983).

65. A.I. Konukhov, L.A. Melnikov, “Optical vortices in a vector field: the general definition based on the analogy with topological solitons in a 2D ferromagnet, and examples from the polarization transverse patterns in a laser”, J. Opt. B: Quantum Semiclass. Opt. Vol. 3, S139–S144, (2001).

66. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, M.O. Sopin, “About thin structure of speckle field”, SPIE Proc., Vol. 2647, pp. 75-79, (1995).

67. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, M.O. Sopin, “About thin structure of speckle field”, SPIE Proc., Vol. 2778, pp. 357-358, (1996).

68. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, “Study of statistical fields in vicinity of zero-crossing” SPIE Proc., Vol. 3317, pp. 88-96, (1997).

69. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, “About thin structure of speckle field in the vicinity of small amplitudes”, Opt. and Spectroscopy, Vol. 82, pp. 621-629, (1997).

70. I. Mokhun, M. Sopin, “Thin structure of coherent optical fields in the vicinity of minimal intensity and its connection with wave front dislocations” SPIE Proc., Vol. 3317, pp. 108-110, (1997).

71. J.F. Nye, J.V. Hajnal, “The wave structure of monochromatic electromagnetic radiation”, Proc. R. Soc. Lond., Vol. A 409, pp. 21-36, (1987).

72. A. Apostol, A. Dogariu, “First- and second-order statistics of optical near fields”, Opt Lett., Vol. 29, pp. 235-237, (2004).

73. J. Ellis, A. Dogariu, “Discrimination of globally unpolarized fields through Stokes vector element correlations” J. Opt. Soc. Am A, Vol. 22, pp. 491-496 (2005).

74. A. Dogariu, E. Wolf, “Coherence theory of pairs of correlated wave fields”, Journ. of Modern Opt., Vol. 50, 1791-1796, (2003).

75. J.V. Hajnal, “Singularities in the transverse fields of electromagnetic waves I. Theory”, Proc. R. Soc. Lond., Vol. A 414, pp. 433-446, (1987).

76. J.V. Hajnal, “Singularities in the transverse fields of electromagnetic waves II”, Proc. R. Soc. Lond., Vol. A 414, pp. 447-468, (1987).

77. J.V. Hajnal, “Observation of singularities in the electric and magnetic fields of freely propagating microwaves”, Proc. R. Soc. Lond., Vol. A 430, pp. 447-468, (1987).

78. R.M.A. Azzam, N.M. Bashara, “Ellipsometry and Polarized Light”, North-Holand, (1977).

79. O. Angelsky, A. Mokhun, I. Mokhun, M. Soskin, “The relationship between topological characteristics of component vortices and polarization singularities”, Opt. Comm., Vol. 207, pp. 57-65, (2002).

80. O. Angelsky, R. Besaha, A. Mokhun, I. Mokhun, M. Sopin, M. Soskin, M. Vasnetsov, “Singularities in vectoral fields”, SPIE Proc., Vol. 3904, pp. 40-55, (1999).

81. O.V. Angelsky, R.N. Besaha, I.I. Mokhun, M.O. Sopin, M.S. Soskin, “Singularities in vector fields”, Nauk. Visn. Cherniv. Univ., Vol. 57, Physics, Electronics, pp. 88-99, (1999).

82. O.V. Angelsky, A.I. Mokhun, I.I. Mokhun, M.S. Soskin, “Interferometric methods in diagnostics of polarization singularities”, Phys. Rev. E., Vol. 65, 036602(5), (2002).

83. O.V. Angelsky, A.I. Mokhun, I.I. Mokhun, M.S. Soskin, “Inerferometric methods in diagnostics of polarization singularities”, SPIE Proc., Vol. 4829, pp. 487-488, (2002).

84. A.I. Mokhun, M.S. Soskin, I. Freund, “Elliptic critical points: C-points, a-lines, and the sign rule”, Opt. Lett., Vol. 27, pp. 995-997, (2002).

85. I. Freund, M.S. Soskin, A.I. Mokhun, “Elliptic critical points in paraxial optical fields”, Opt. Comm., Vol. 207, pp. 223-253, (2002).

86. I. Freund, “Second harmonic generation of optical ellipse fields”, Opt. Comm., Vol. 213, pp. 129-149, (2002).

87. I. Freund, “Polarization singularity indices in Gaussian laser beams”, Opt. Comm., Vol. 201, pp. 251-270, (2002).

88. O.V. Angelsky, R.N. Besaha, A.I.Mokhun, I.I. Mokhun, M.S. Soskin, “Elementary polarization singularities”, Nauk. Visn. Cherniv. Univ., Vol. 63, Physics, Electronics,pp. 45-51, (1999).

89. Van de Hulst, “Light Scattering by Small Particles”, A.Wiley Interscience Publication, John Wiley and Sons, (1957).

90. D.I. Mirovicki, I.F. Budyagin, V.F. Dubrovin, “Microwave Optics and Holography”, Moscow, Nauka, (1983).

91. G.G. Abezgaus, A.P. Tron’, Yu.N. Kopenkin, I.A. Korovina, “Handbook on the Statistical Computation”, Moscow, Voenizdat, (1970).

92. M. Nieto-Vesperinas, “Scattering and Diffraction in Physical Optics”, A Wiley-Interscience Publication, John Wiley and suns, Inc., (1981).

93. I. Freund, A.I. Mokhun, M.S. Soskin, O.V. Angelsky, I.I. Mokhun, “Stokes singularity relations”, Opt. Lett., Vol. 27, pp. 545-547, (2002).

94. I. Freund, “Polarization flowers”, Optics Comm., Vol. 199, pp. 47-63, (2001).

95. L. Allen, M.J. Padgett, M. Babiker, “The Orbital Angular Momentum of Light”, E.Wolf, Progress in optics XXXIX, Elsevier Science B.V., (1999).

96. L. Allen, M.J. Padgett, “The Poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density”, Opt. Comm., Vol. 184., pp. 67-71, (2000).

97. H. He, M.E.J. Friese, N.R. Heckenberg, H. Rubinsztein-Dunlop, “Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity”, Phys. Rev. Letters, Vol. 75, pp. 826-829, (1995).

98. K.N. Gahagan, G.A. Swartzlander, “Optical vortex trapping of particles”, Opt. Lett., Vol. 21, pp. 827-829, (1999).

99. Matthew J.Lang, Steven M. Block. “Resource Letter: LBOT-1: Laser-based optical tweezers”, Am. J. Phys., Vol. 71, pp. 201-215, (2003).

100. M. Berry, “Paraxial beams of spinning light”, Proc. SPIE, Vol. 3487, pp. 6-11, (1998).

101. V.I. Arnold, “Catastrophe Theory”, second revised and expended edition Berlin, Springer, (1986).

102. I. Mokhun, A. Arkhelyuk, R. Brandel, Ju. Viktorovskaya, “Angular momentum of electromagnetic field in areas of optical singularities” SPIE Proc., Vol. 5477, pp. 47-54, (2004).

103. I. Mokhun, A. Mokhun, Ju. Viktorovskaya, D. Cojoc, O. Angelsky, E. Di Fabrizio, “Orbital angular momentum of inhomogeneous electromagnetic field produced by polarized optical beams”, Proc. SPIE, Vol. 5514, pp. 652-662, (2004).