1.4.6.4. Analysis of the averaged parameters for the field decomposition into circular basis
It known, the structure of the -components of the field depend on the orientation of the decomposition basis. In part, the obligatory condition of the above consideration consists in the choice of the decomposition basis, where intensities of the orthogonal components are equal. On the other hand, the structure of the orthogonal field components does not depend on orientation of the basis of decomposition, if the field is represented as a superposition of orthogonally circularly polarized components. In this case, a phase difference of the components is directly connected with the azimuth of polarization (1.49), and the saddle points of a phase difference are the saddle points of the azimuth. Thus, consider decomposition of non-uniformly polarized fields into circular basis.
A coherence matrix for the circular basis of decomposition has the form:
,
(1.143)
where
etc. (
being the amplitudes of the circularly polarized components) are
randomly distributed in space. In this case, localization of the
phase difference vortices coincide with localization of
-points
(see subsection 1.3.1).
Stokes parameters written in terms of such matrix are of the form:
. (1.144)
Performing analysis similar to the case of the field decomposition into linear basis, one obtains the following representation of Stokes parameters:
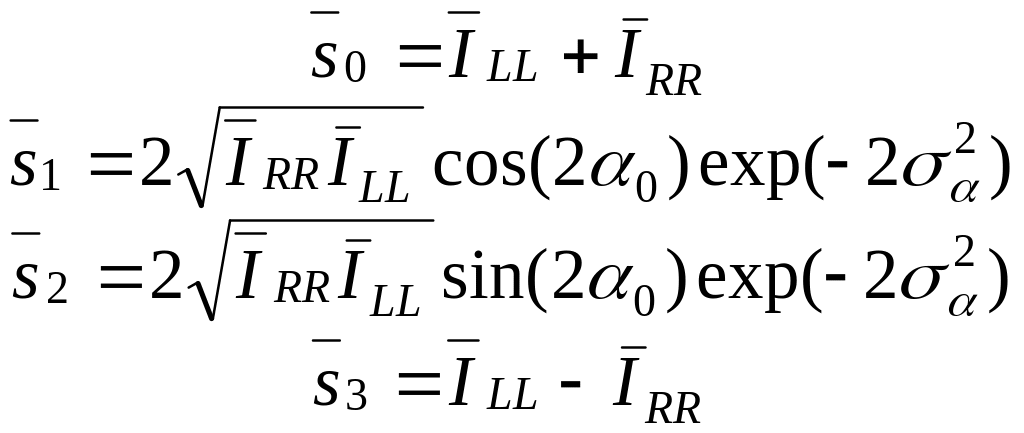, (1.145)
where
,
are the average intensities of the clockwise and the counterclockwise
components, respectively,
is the prevailing azimuth of polarization, and
in the dispersion of the azimuth of polarization at the saddle points
of azimuth.
For the circular basis of decomposition the following relation is also true:
,
(1.146)
i.e. an
integral depolarization takes place. Equality in Eq. (1.146) takes
place, if
,
viz. For completely and uniformly polarized fields. One can see from
Eq. (1.145), which is similar to Eqs. (1.136, 1.137), that the
averaged Stokes parameters can be determined by measuring dispersion
of the azimuth of polarization at the saddle points of azimuth. It
follows from this equation that one can determine dispersion of the
azimuth of polarization at the field areas with prevailing
polarization of non-uniformly polarized vector field from the known
Stokes parameters. Note, dispersion of the azimuth of polarization
can be now represented as the function of a distance between the
adjacent vortices of the same sign,
,
belonging to the orthogonally linearly polarized components of a
field.
1.4.6.5. Comparison of the experimental results and the data of computer simulation
Stokes parameters and a mean distance between the adjacent vortices of the same sign belonging to the orthogonal components were not only obtained by a computer simulation but also experimentally determined for various levels of depolarization. Thin light-scattering polymeric films were used as the test-objects. Depolarization of the field scattered by such films was at the levels close to the ones used in computer simulation.
Experimental arrangement is shown in Figure 1.46. A circularly polarized beam enters the Mach-Zehnder interferometer. A thin polymeric film is placed at one leg of the interferometer, at the focal plane of the objective 10. Such arrangement provides the analysis of the scattered field within small enough solid angle and, besides, formation of the field at far zone with the corresponding scale of speckles just behind the objective. A Stokes-polarimeter is placed at the interferometer output for measuring the averaged Stokes parameters. Circularly polarized reference beam and a polarizer 13 provide determination of the position and the sign of the each component vortex by applying the technique described in Ref. [82,83]. For that, the size of the sensitive area of a photodetector satisfies Eq. (1.113). Thus, we realize the feasibilities for measuring the averaged polarization parameters and obtaining the nets of the vortices of the orthogonal components in parallel.
T
he
component vortices of opposite signs can be identified on the
corresponding interference patterns, cf. Figure 1.50, viz. as the
oppositely directed interference forklets. In such a manner, we
obtained the nets of the component vortices for various objects
providing various level of depolarization of the scattered field. We
also determined the mean distances between the adjacent vortices of
the same sign belonging to the orthogonal components.
The experimental results and the results of computer simulation of the vector field are shown in Figures . 1.51 and 1.52 for various depolarization degrees of the scattered field.
F
Figure
1.50
,
(1.147)
where
is the density of vortices of any of orthogonal components [8,12].
Figure 1.54
illustrates the dependence of Stokes parameters
and
on the ratio of the mean distance between the component vortices of
the same signs to the correlation length.
One can see that all dependencies are almost linear, and good correspondence of the experimental and simulated data takes place.
а b
Fig. 1.51
Simulation results: positions of the vortices associated with the
orthogonal components for various levels of depolarization of the
field indicated by the numbers at the upper left corners.
,
and,
,
– positions of the vortices of the orthogonal components;
,
– positive vortices,
,
–negative vortices.
c d
Figure 1.51. Experimental data: positions of the vortices associated with the orthogonal components for various levels of depolarization of the field indicated by the numbers at the upper left corners. , and, , – positions of the vortices of the orthogonal components; , – positive vortices, , –negative vortices.
а b
c d
Figure 1.52. Data of computer simulation: positions of the vortices associated with the orthogonal components for various levels of depolarization of the field indicated by the numbers at the upper left corners. , and, , – positions of the vortices of the orthogonal components; , – positive vortices, , –negative vortices.
Figure
1.53.
Interconnection of the level of depolarization with the distance
between the vortices.
– experimental data;
– results of computer simulation.
Figure
1.54.
Dependence of Stokes parameters
and
on the distance between the component vortices of the same sign.
– experimental data;
– results of computer simulation base on Eq. (1.137));
– results of computer simulation obtained by the averaging of the
local Stokes parameters.
Thus, the
characteristics of polarization singularities, the systems of
singular and stationary points (phase difference vortices,
points,
saddle points of a phase difference,
and the azimuth of polarization) not only determine in qualitative manner the behavior of the vector field at each point, but are unambiguously connected with the averaged polarization characteristics of the vector field.
Dispersion of the phase difference between the orthogonal components corresponding to various levels of integral depolarization of a vector field is the function of a mean distance between the adjacent vortices of the same sign belonging to different linearly polarized orthogonal components. As a result, the averaged Stokes parameters and dispersion of the azimuth of polarization can be found out by determining such distance.
The size of the areas with large changes of the polarization parameters is determined by the level of integral depolarization alone. At the same time, the size and the positions of -contours for levels of depolarization no exceeding 50% depend also on the prevailing phase difference between the components. Size of -contours is minimal for prevailing circular polarization. If the level of depolarization exceeds 50%, a fine structure of the field becomes similar to the fine structure of completely depolarized fields and does not depend on the prevailing phase difference between the orthogonal components.