1.4.2.3. Vortices of orthogonally polarized field components. Technique for study of polarizatioN singularities

Consider any area of the field bounded by -contour. Let us represent as a superposition of counterclockwise and clockwise circular field components [3,78]. It follows from Eq. (1.49) that

, (1.65)

or

. (1.66)

Consider changing the vibration phase along -contour.

The each component is characterized by any phase distribution. While the vortices of the circularly polarized components can be put in correspondence to -points of the field,, as it is seen in subsection 1.4.1, the positions of the vortices of circularly polarized components are found in the areas of a vector field that are characterized by opposite polarization (clockwise or counterclockwise), i.e. these vortices are separated into space. As a consequence, the regions where the phases of the components are changed most rapidly are also spatially separated, while these regions are drawn toward the vortices. On this reason, one can conclude that changing of the phases of the components within -contours is relatively slow (at least, in statistical sense), so that the derivatives of phases of the components along -contour, and ( is the parameter of the contour arc) are relatively small.

It is known [75] that at points of -contour where derivative of the vibration phase, , i.e. at points of the phase extrema, the points of birth and annihilation of disclinations occur. On the other hand, it follows from Eq. (1.65) that

, (1.67)

or

. (1.68)

A

Figure 1.27

s a consequence, assuming that both and are small, one expects to observe the extrema of the azimuth of polarization in the nearest vicinity of the points of birth and annihilation of disclinations.

Such points of -contour are easily identified by analysis of the vortex nets for linearly polarized projections of a vector field.

The part of -contour is shown in Figures 1.27(a)-(e). Figure 1.27(a) illustrates behavior of the azimuth of linear polarization within this part. Changing the azimuth along -contour is sketched in Fig 1.27(f). One can see from Figures 1.27(a) and (f) that azimuth reaches a local minimum at point 3. Using a rotating polarizer, we can select various linearly polarized projections of the field. The rotation direction is depicted by the arrow at the right side of Figure 1.27(a).

Figures 1.27(b)-(e) correspond to four different orientations of a polarizer. Orientations of its axis are shown by bold arrows at right sides of these figures. In situation shown in Figure 1.27(b) the polarizer is crossed with the polarization in points 1’ and 1’’. In this case, the vortices of the corresponding polarization projection occur in these points. The vortices can be identified by interference of the polarization projection of a field with a reference wave. Then, one observes interference forklets at the vortices loci. Further rotation of a polarizer (Figure 1.27(c)) leads to shifting the vortices of the projection along -contour from positions 1’ and 1’’ to the positions 2’ and 2’’. At last, for orientation of a polarizer shown in Figure 1.27(d), the vortices merge and annihilate. Further (even if small) rotation of a polarizer leads to the situation when none vortex is observed at this part of -contour, Figure 1.27(e).

Using this technique, one can “visualize” a disclination at arbitrary point of -contour. Consider a decomposition of into orthogonal components . Let us fix any axis of coordinates at any point of -contour along the vector . Then, one of the components (to say, ) equals zero at each instant, i.e. the vortex of this component occurs. The transversal component of the electrical field is described at this point as follows:

. (1.69)

Thus, as one of the axes of the decomposition basis is collinear to the vector , the condition of disclination at this point of -contour takes the form:

(1.70)

The condition of disclination given in Ref. 75 is of the form:

(1.71)

corresponding to the instant 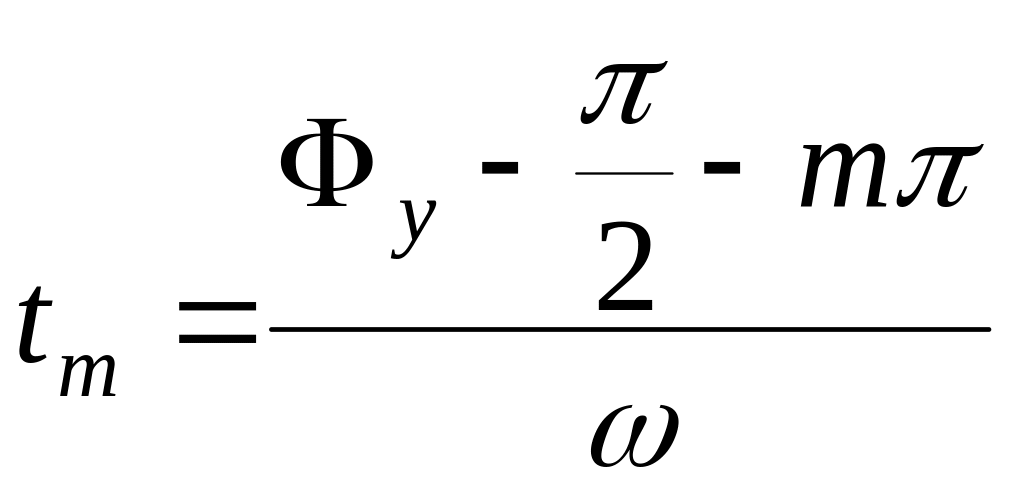. can be determined interferentionally (of course, within the phase of reference wave) by rotating a polarizer at 90 degrees. Let us rotate a polarizer at small angle in respect to its initial orientation. It results in displacement of the vortex associated with the -component along -contour that provides a possibility to visualize a disclination at any other instant. Thus, one can establish the correspondence among the position of disclination at -contour (as a function of time), on the one hand, and the position of a vortex (as a function of the spatial coordinates), on the other hand.

Comparing Eqs. (1.70) and (1.71) one can see that at -contour. As so, one can use a polarizer transmitting the component of with the azimuth parallel to the -axis, and observe the vortex of the -component. In such a manner, one “visualize” a disclination.

T

Figure 1.28. Arrangement for observation of the points of birth and annihilation of the vortices at polarization projection of the field. 1, 11 – beamsplitters, 2 – microobjective, 3 – tephlon plate, 4 – objective, 5,6 – mirrors, 7 – -plate, 8,9,10 – beam-expanders, 12 – analyzer.

he processes of birth and annihilation of vortices at polarization projections of the field are experimentally observed using the arrangement of a Mach-Zehnder interferometer shown in Figure 1.28 [80-83]. A tephlon plate 3 (media where multiple light-scattering is realized) is introduced into the object beam, namely, at the focal plane of an objective 2. If this plate is thin enough, the longitudinal coherence of the radiation from a He-Ne laser is preserved. The focused beam illuminates limited number of the scattered centers. In this case, size of a light speckle behind the scatterer is the same as the caustic net of the focused beam. The object is in the front focal plane of the objective 4, which forms quasi-parallel beam (far-field approximation is admissible). At the plane one observes interference between this beam and the reference one. A -plate is placed in the

Figure 1.29. Experimental determination of the positions of birth and annihilation of the vortices at polarization projections. White arrow at left side of the each fragment is the spatial mark. Interferograms in fragments (a)-(f) correspond to various orientation of the axis of polarizer 12. s-contour is shown in fragment (f) by a white line.

reference leg to convert a linear polarization into circular one. Controlled analyzer 12 is used at the interferometer output to select desirable projection of the object beam and the reference one.

Experimental results are shown in Figure 1.29. White arrows at left side of the fragments serve as the spatial mark. In Figure 1.29(a), all interference fringes are continuous. For a small rotation of the axis of an analyzer 12, one observes characteristic bending of an interference fringe that put in evidence rapid changing the phase within this region of the field. For further rotation of an analyzer, the fringe is broken that corresponds to the birth event (Fig.1.29(c)). A local extremum of the azimuth is observed at this point, in accordance with the above consideration. One can also observe in this fragment that a new vortex, , enters the analyzing zone (down directed interference forklet). Further rotation of an analyzer results in motion of the vortices of opposite signs ( ) in opposite directions, see Figure 1.29(d). Here one can see also, within the region bounded by a white rectangle, a new bifurcation of an interference fringe associated with the point of birth of once more vortex pair. In Figure 1.29(e), within the region depicted by a rectangle, vortex has been annihilated with the vortex born at right side, and the vortex moves to the vortex . Figure 1.29(f) corresponds to the case, when the vortices and annihilate, and one observe continuous interference fringes throughout the observation plane, excluding the region of the vortex , which moves to the left angle of an interferogram. -contour is shown here be a white line.

1.4.2.4. -points as the phase difference vortices

Let us decompose a vector field into orthogonally circularly polarized components. In this case, we also obtain a complete system of the vortices (superposition of two vortex nets), analysis of which provides establishing the interconnections among the component vortices and the vector singularities. Such decomposition, however, possesses some peculiarities.

1. As it is known, the phase difference of the components does not depend on the orientation of the decomposition basis.

2. -points play the role of a phase difference vortices (see subsection 1.4.2.1).

3. Following to Eq. (1.49), the contours of a phase difference correspond to the lines of the constant azimuth of polarization.

For such decomposition of the field, -contours are the lines determined by the solutions of the equation . Similarly to the case of decomposition of the field into linearly polarized components, one can put in correspondence the topological charges to the circularly polarized components of the phase difference vortices. Topological charge of such vortex coincides in sign with the topological sign of the vibration phase in the vicinity of -point, while its module is doubled.

It is evident (accounting Eqs. (1.48) and (1.49)), for -points as the phase difference vortices, one can formulate the sign principle, which is the analogue of the sign principle for phase vortices of a scalar field, as well as for phase difference vortices obtained in the case, when a vector field is decomposed into orthogonally linearly polarized components [81,84-87]: (i) the even number of -points are at the closed equiazimuthal line; (ii) the adjacent -points at some equiazimuthal line possess the indices of opposite signs.

For that, the following topological invariants take place:

1. The number of -points (phase difference vortices) with the topological index of the same sign equals the number of -points (number of vortices) of the opposite sign:

. (1.72)

2. The number of saddle points of the field of azimuths is connected with the number of extrema of the azimuth of polarization and -points as

. (1.73)

T

Figure 1.30. 1,2 – -contours; – points of extremum of the azimuth of linear polarization; – -points (phase difference vortices); – saddle point of azimuth of polarization (phase difference saddle).

he number of extrema of the azimuth of polarization (difference phase extrema) is much less than the number of -points and saddles. It follows from the properties of the evaluating scalar field , which can be introduced by analogy with the decomposition of the field into linearly polarized components.

Negligible number of extrema of the azimuth of polarization as the points where the azimuth reaches its maximal or minimal magnitude does not contradict to the presence of local extrema of the azimuth of linear polarization along -contour, as it is seen from Figure 1.30. In this figure, the broken lines designate -contours, and the dashed-dotted lines (with one and two dots) designate the tangent to them equiazimuthal lines. One can see that the local extrema of the azimuth of linear polarization are just at these points .