7. Понятия интегральной суммы и определенного интеграла. Свойства определенного интеграла

Интегральная сумма. Пусть функция y = f(x) определена на отрезке ,a < b. Разобьем этот отрезок на n произвольных частей точками:

a = x₀ < x₁ < x₂ < … < x_i-1 < x_i < … < x_n = b.

В каждом из полученные отрезков выберем произвольную точку_i. Через х_i обозначим разность x_i – x_i-1, которую условимся называть длиной частичного отрезка . Образуем сумму:

 = f (₁) x₁ + f(₂) x₂ + … + f (_n) x_n = ,

которую назовем интегральной суммой для функции f (x) на , соответствующей данному разбиению на частичные отрезки и данному выбору промежуточных точек_i.

Определенный интеграл. Обозначим через  длину наибольшего частичного отрезка x_i данного разбиения. Определенным интегралом от функции f(x) по отрезку называется конечный пределI интегральной суммы , если такой предел существует:

В случае, если такой предел существует, функция называется интегрируемой на .

Свойства определенного интеграла.

1. Из определения определенного интеграла следует а) если a = b, то

;

б) если поменять местами пределы, то определенный интеграл поменяет знак:

2. Какие бы ни были числа a, b, c, имеет место равенство:

. *)

Доказательство: допустим сначала, что a < b < c. Так как предел интегральной суммы  не зависит от способа разбиения отрезка , то будем разбивать отрезоктак, чтобы точка с была точкой разбиения. Если, например, с =x_m, то  можно разбить на две суммы:

.

Переходя к пределу при   0, получаем равенство *). Доказательства для других случаев расположения точек а, b, c легко сводятся к рассмотренному случаю с помощью первых двух свойств.

3. Постоянный множитель можно выносить за знак определенного интеграла.

Доказательство: для любого разбиения отрезка и для любого выбора точек_i

.

Переходя к пределу при   0, имеем

.

4. Определенный интеграл от алгебраической суммы функций равен сумме их интегралов. Действительно, для любого разбиения отрезка 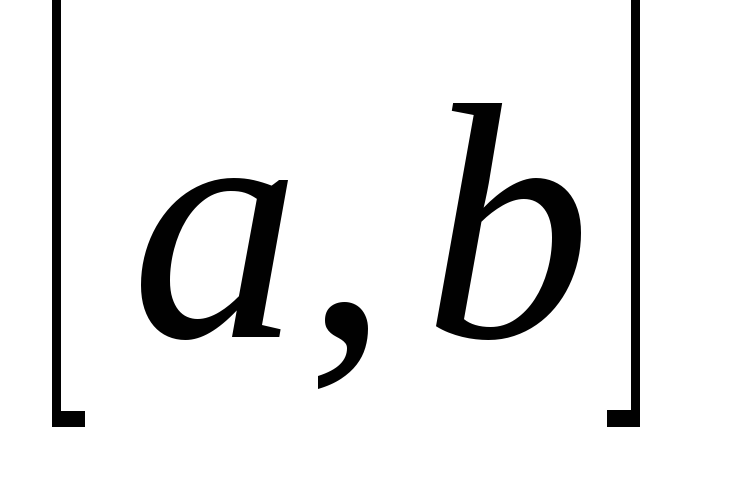и любого выбора точек_i:

Замечание: свойство №4 имеет место для любого конечного числа слагаемых.

5. Если всюду на отрезке функцияf(x)  0, то

.

Доказательство: в самом деле любая интегральная сумма для функции f(x)  0 на отрезке неотрицательна, т.к.f(_i)  0, x_i = x_i – x_i-1 > 0, i = 1, 2, …, n. Переходя к пределу при   0 в неравенстве , получаем:

.

6. Если всюду на отрезке f(x) g(x), то

.

Согласно свойству №5 для функции f(x) – g(x):

.

Но согласно свойству №4:

.

Таким образом, получаем неравенство

8. Интегральная теорема о среднем значении

Теорема: если функция f(x) непрерывна на отрезке , то на этом отрезке существует точкаc такая, что

Доказательство: так как функция f(x) непрерывна на , то по второй теореме Вейерштрасса существуют числаm и M такие, что

Применяя 6-е свойство определенных интегралов, запишем

Заметим, что

Отсюда получаем соотношение

Положим 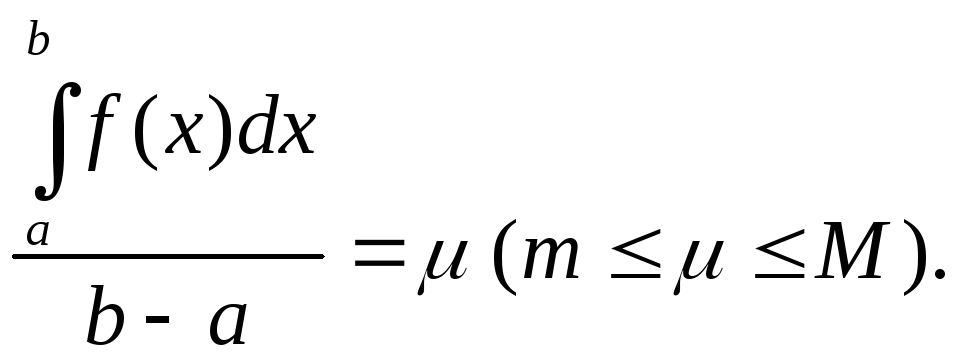Так как число заключено между наименьшим и наибольшим значениями непрерывной функции f(x) на 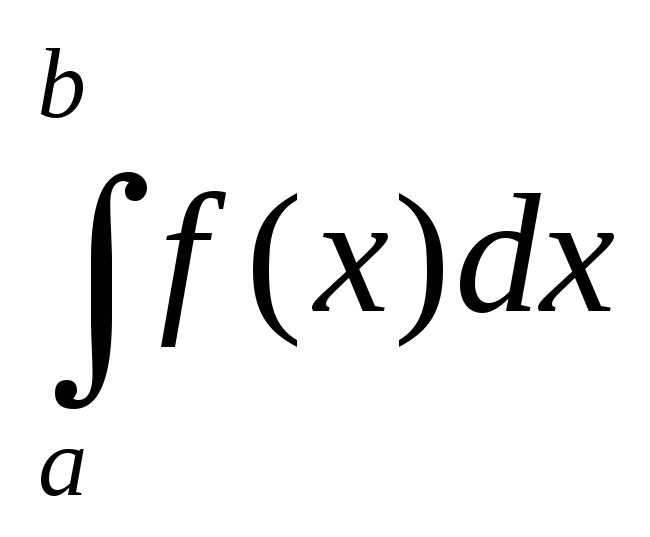, то по теореме о прохождении непрерывной функции через любое промежуточное значение существует точка стакая, чтоf(c) = . Поэтому

Геометрический смысл теоремы состоит в следующем: величина определенного интеграла при f(x)  0 равна площади прямоугольника, имеющего высоту f(c) и основание b – a.