Методические указания по выполнению контрольной работы по дисциплине «МАТЕМАТИКА»

Заочная форма обучения предполагает самостоятельную работу студента над учебным материалом: поиск, анализ и оценка информации по содержанию учебного материала, решение задач, выполнение контрольных заданий. Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса «Математика», используя учебные задания, Интернет-ресурсы, дополнительную литературу.

При выполнении контрольной работы студент должен руководствоваться следующими указаниями:

• Контрольная работа выполняется в отдельной тетради в клетку, на титульном листе которой должны быть ясно написаны фамилия студента, его инициалы, курс, специальность и вариант

• Задачи следует располагать в порядке номеров, указанных в заданиях. Перед решением необходимо полностью переписать её условие.

• Ход решения каждой задачи студент обязан оформить аккуратно

• На каждой странице тетради необходимо оставить поля шириной 3-4 см для замечаний преподавателя

• Контрольная работа выполняется самостоятельно.

• Вариант выбирается в соответствии с номером в журнале.

Вариант контрольной работы	Номер студента по журналу
	1, 8, 15, 22
	2, 9, 16, 23
	3, 10, 17, 24
	4, 11, 18, 25
	5, 12, 19, 26
	6, 13, 20, 27
	7, 14, 21, 28

Задания контрольной работы №2

ВАРИАНТ 1

1. Показать на числовой прямой множества

А=[-10,3];B[-¥;2]. Найти объединение, пересечение, разность.

2. Известно, что высказывание a,b – истины, c – ложно. Определить истинное ли высказывание .

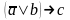3. Дано множество А={x:x³-6x²+9x=0}. Перечислите элементы множества и подмножества. Какова мощность данного множества.

4. Является ли истинным высказывание «Для любых множеств А, В, С выполняется (А\В)È(В\А)=(АÈВ)\(АÇВ\ (АÈВ)». Объяснить с помощью диаграммы Венна.

5. Даны предложения.

   1. {a,b,c}={b,c,a}

   2. 66³6·6

   3. 

   4. 10 делится на 3 тогда и только тогда, когда 100 делится на 9.

   5. Если 5<-1, то 3²=9.

   6. График функции у=х прямая или парабола.

   7. 25 делится на 5 и на 2.

   8. Привет!

Укажите номера простых, сложных, неопределенных высказываний. Какие предложения не являются высказываниями. Установите истинность простых высказываний. Для сложных высказываний установите логические операции и истинность. Сформулируйте для простых высказываний отрицание, конъюнкцию и дизъюнкцию для простых высказываний.

6. Составьте таблицу истинности для выражения .

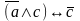7. Произведя 100 выстрелов, стрелок попал в цель 68 раз. Найти вероятность того, что цель будет поражена.

8. В упаковке в 6 раз больше синих стержней, чем красных. Найти вероятность того, что выбранный наугад стержень окажется красным.

9. Два рыбака ловят рыбу на берегу озера. Вероятность того, что поймает первый –0,4, второй – 0,8. Найти вероятность того, что хотя бы один поймает рыбу.

10. Стрелок попадает в мишень в 8 случаях из 10. Найти вероятность того, что он 2 раза не попадёт из 5 выстрелов?

11. Произведя 90 выстрелов, стрелок попал в цель 65 раз. Найти вероятность того, что цель будет не поражена.

12. Три рыбака ловят рыбу на берегу озера. Вероятность того, что поймает рыбу первый –0,4, второй – 0,6, второй – 0,5. Найти вероятность того, что только один поймает рыбу.

13. На посту стоит 6 солдат. Вероятность, не заснуть на посту, для каждого равна 0,4. Какова вероятность того, что 4 из 6 не заснут?

Вариант 2.

1. Показать на числовой прямой множества

А=[-¥,5];B[-10;3]. Найти объединение, пересечение, разность.

2. Известно, что высказывание a,b – истины, c – ложно. Определить истинное ли высказывание .

3. Дано множество А={x:x³+2x²+x=0}. Перечислите элементы множества и подмножества. Какова мощность данного множества.

4. Является ли истинным высказывание «Для любых множеств А, В, С выполняется А\ (А\В)=АÇВ». Объяснить с помощью диаграммы Венна.

5. Даны предложения.

1. 70£7·6

2. 

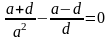
3. 25 делится на 5 тогда и только тогда, когда 100 делится на 2.

4. Если 5>-1, то 2²=4.

5. С новым годом!

6. 30 делится на 5 или на 4.

7. Бабочка и паук – насекомые.

Укажите номера простых, сложных, неопределенных высказываний. Какие предложения не являются высказываниями. Установите истинность простых высказываний. Для сложных высказываний установите логические операции и истинность. Сформулируйте для простых высказываний отрицание, конъюнкцию и дизъюнкцию для простых высказываний.

6. Составьте таблицу истинности для выражения .

7. Для контроля качества на птице фабрике выбрали 100 яиц. 45 из них оказались первого сорта. Какова вероятность того, что взятое наугад яйцо окажется первого сорта.

8. В коробке в 6 раза больше тетрадей в клетку, чем в линейку. Найти вероятность того, что выбранное наугад тетрадь окажется в линейку.

9. Студенту надо написать два реферата. Вероятность того, что он напишет первый – 0,9, второй – 0,8. Какова вероятность того, что студент напишет хотя бы один реферат.

10. Куплено 10 телевизоров одной фирмы. Вероятность того, что телевизоры в течение времени Т каждый из телевизоров будет работать, равна 0,9. Определить вероятность того, что за время Т 2 телевизора будут нуждаться в ремонте.

11. Для контроля качества на птице фабрике выбрали 90 яиц, 35 из них оказались первого сорта. Какова вероятность того, что взятое наугад яйцо окажется не первого сорта.

12. Студенту надо написать три реферата. Вероятность того, что он напишет первый – 0,7, второй – 0,8, третий – 0,4. Какова вероятность того, что студент напишет только один реферат.

13. Вероятность, поехать отдыхать по путёвке для студента, равна 0,3. Какова вероятность того, что поедут отдыхать 2 человека из 5?

Вариант 3.

1. Показать на числовой прямой множества

А=[-15,¥];B[-1;10]. Найти объединение, пересечение, разность.

2. Известно, что высказывание a,b – истины, c – ложно. Определить истинное ли высказывание .

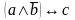3. Дано множество А={x:x³-10x²+25x=0}. Перечислите элементы множества и подмножества. Какова мощность данного множества.

4. Является ли истинным высказывание «Для любых множеств А, В, С выполняется (А \В)È(В\А)=ВÇА». Объяснить с помощью диаграммы Венна.

5. Даны предложения.

1. Если 20 делится на 3, то 20 делится на 5.

2. 66³6·6

3. 

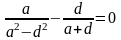
4. 10 делится на 3 тогда и только тогда, когда 100 делится на 9.

5. 5<-1, тогда и только тогда, когда 3²=6.

6. График функции у=х² прямая и парабола.

7. 15 делится на 5 ил на 2.

8. Какой сегодня день?

Укажите номера простых, сложных, неопределенных высказываний. Какие предложения не являются высказываниями. Установите истинность простых высказываний. Для сложных высказываний установите логические операции и истинность. Сформулируйте для простых высказываний отрицание, конъюнкцию и дизъюнкцию для простых высказываний.

6. Составьте таблицу истинности для выражения .

7. В школе для тестирования выбрали 50 учеников, 10 из них тест не прошли. Какова вероятность того, что наугад взятый ученик не пройдёт тест.

8. При игре в гольф первый игрок попадал в лунку в 4 раза больше, чем второй. Найти вероятность попадания в лунку второго.

9. Ученик не знающий расписание взял с собой химию и физику. Вероятность того, что в этот день будет химия – 0,4 и физика – 0,2. Найти вероятность того, что хотя бы один предмет ученик взял правильно.

10. Мужчина, играющий в гольф, попадает в лунку в 7случаях из 10. Какова вероятность того, что, он 1 раза не попадёт из 4 ударов?

11. В школе для тестирования выбрали 65 учеников, 15 из них тест не прошли. Какова вероятность того, что наугад взятый ученик пройдёт тест.

12. Ученик не знающий расписание взял с собой алгебру, химию и физику. Вероятность того, что в этот день будет алгебра – 0,8, химия – 0,4 и физика – 0,2. Найти вероятность того, что только один предмет ученик взял правильно.

13. Мужчина, играющий в гольф, попадает в лунку в 6 случаях из 10. Какова вероятность того, что, он 3 раза попадёт из 4 ударов?

Вариант 4.