§ 9.6. Коэффициенттері тұрақты сызықты
дифференциалдық теңдеулер жүйесі
1.
Біртекті теңдеулер жүйесі. Сипаттаушы
теңдеу.
Коэффициенттері
тұрақты нақты сандар болатын,
(9.82)
теңдіктер, коэффициенттері тұрақты қалыпты сызықты біртекті дифференциалдық теңдеулер жүйесі деп аталады.
Егер
,
(9.83)
матрицаларын
енгізсек, (9.82)
теңдеулер жүйесін матрица-векторлық
түрге келтіруге болады. Берілген (9.82)
теңдеулер жүйесінің нөлден ерекше
шешімін Эйлер тәсілі бойынша
(9.84)
түрде
іздейміз. Мұндағы
әзірге белгісіз, кейіннен анықталатын
сандар. Бұл шешімдер векторлық түрде
(9.84)
түрін
қабылдайды. Мұндағы
.
Демек,
(9.84)
шешімнің туындысы
болғандықтан,
мәндерін берілген теңдеудегі (матрицалық
түрдегі) орындарына қойсақ,
шамасына қысқартқаннан кейін,
белгісіздері бойынша сызықты біртекті
алгебралық теңдеулер жүйесін
(9.85)
аламыз. Мұндағы
бірлік матрица. Алынған бұл теңдеулер
жүйесінің нөлден ерекше шешімінің болуы
үшін, сәйкес анықтауыштың нөлге тең,
яғни
(9.86)
болуы
қажетті және жеткілікті шарт болып
табылады. Бұл (9.86)
теңдік (9.82)
теңдеулер жүйесіне сәйкес сипаттаушы
теңдеу, ал алынған
сипаттаушы көпмүшелік деп аталады. Бұл
теңдеуді шешу арқылы
матрицасының
меншік мәндерін аламыз. Табылған меншік
мәндерді (9.85)
теңдеулер жүйесіне қойып, ашып жазсақ
(9.87)
теңдіктерін
аламыз. Осы алынған (9.87)
алгебралық теңдеулер жүйесін, (9.86)
сипаттаушы теңдеудің шешімдерінің
әрбіреуі үшін шешсек,
матрицасының сәйкес
меншік векторларын аламыз.
Сонымен,
жоғарыдағы (9.84)
функциялар, берілген (9.82)
теңдеулер жүйесінің шешімдері болуы
үшін,
сандары
матрицасының меншікті мәні болатын
санына сәйкес табылған
меншік векторының координаталары
болуы, қажетті және жеткілікті шарт
болады.
Жоғарыдағы сипаттаушы (9.86) теңдеудің сол жағында -ға байланысты - ші ретті сипаттаушы көпмүшеліктің әртүрлі түбірлері болады 1. Сипаттаушы теңдеудің түбірлері әртүрлі және нақты сандар 2. Сипаттаушы теңдеу түбірлерінің ішінде комплекс сандар да кездеседі 3. Сипаттаушы теңдеу түбірлерінің ішінде еселі түбірлер кездеседі.
Енді осыларға жеке-жеке тоқталайық.
1.
Теңдеудің
түбірлері әртүрлі және нақты сандар
болса, онда осы оқулықтың І-бөліміндегі
меншік векторлардың 1-
қасиеті бойынша,
матрицасының өзара сызықты тәуелсіз
меншікті векторлары болады. Мұндағы
.
Онда (9.93)
теңдеулер жүйесінің шешімі
(9.88)
вектор - функция түрін қабылдайды.
Енді
(9.88)
функцияларының сызықты тәуелсіз
екендігін көрсетсек, онда олардың
берілген теңдеулер жүйесінің шешімдер
базисін құрайтындығы белгілі. Шынында
да,
болғанда ерекше емес, себебі оның
бағандары өзара тәуелсіз
меншікті векторларынан құралған. Ендеше,
Остроградский -
Лиувилль теоремасы
бойынша
үшін
матрицасы ерекше емес. Онда 9.6-
теорема бойынша
вектор-функция өзара сызықты тәуелсіз.
Сонымен, сипаттаушы (9.86) теңдеудің түбірлері әртүрлі және нақты сандар болғанда, (9.82) теңдеулер жүйесінің жалпы шешімінің векторлық түрі
(9.89)
немесе координаттық
(9.89)
түрде жазылады.
М.32.
теңдеулер
жүйесін шешейік.
Шешуі. Сәйкес сипаттаушы теңдеу құрып, оның шешімдерін табамыз
.
Енді оларға сәйкес меншік векторларды қарастырайық.
1.
. Онда (9.87)
бойынша
меншік
векторларды аламыз. Егер
.
2.
.
3.
.
Сонымен, (9.100) және (9.100) бойынша
немесе
2. Сипаттаушы теңдеудің түбірлері әртүрлі және кейбіреулері комплекс сандар болсын.
Айталық,
болғанда, оның түйіндесі
саны да, сипаттаушы теңдеудің түбірі
болып табылады. Себебі, сипаттаушы
теңдеудегі коэффициенттер нақты сандар.
Өз кезегінде, комплекс шешімдерге сәйкес
меншік векторлардың координаталары да
түйіндес-комплекс сандар болады. Шынында
да,
матрицасының элементтері болатын
нақты сандар, онда
.
Ендеше,
және
теңдіктері орындалады.
Айталық,
меншік мәнге сәйкес, меншік вектор
болсын. Онда (9.95)
теңдіктерге сәйкес
(9.90)
вектор - функциясы, берілген (9.102) теңдеулер жүйесінің шешімі болады. Ендеше, Эйлер формуласы бойынша
Бұл
теңдіктің оң жағындағы өрнектің нақты
,
жорамал
бөліктері берілген теңдеулер жүйесінің
өзара тәуелсіз шешімдері болып табылады.
Сонымен,
сипаттаушы теңдеудің түйіндес-комплекс
түбірлеріне 
,
берілген теңдеудің нақты екі шешімі:
;
сәйкес келеді.
Ì.33.
теңдеулер
жүйесін шешейік.
Шешуі.
Сәйкес сипаттаушы
теңдеудің түйіндес-
комплекс түбірлері
болады.
Енді
(9.87) теңдеулер жүйесін құру арқылы,
меншік мәнге сәйкес, меншік векторларды
қарастырайық.
Демек,
.
Онда (9.101)
теңдік бойынша, қвжетті шешімді аламыз
Мұндағы
.
Онда векторлық түрдегі берілген теңдеулер жүйесінің жалпы шешімі
немесе
координаттық түрде 
болып жазылады.
3.
Сипаттаушы
теңдеудің
түбірлерінің кейбіреулері
еселі, мысалы
болғанда, берілген (9.93)
теңдеулер жүйесінің шешімін 
(9.91)
түрде
іздейміз. Мұндағы
өлшемді,
кейіннен анықталатын векторлар. Бұл
шешім координаталар арқылы
(9.92)
түрін
қабылдайды. Мұндағы
сандары, соңғы (9.92) шешімдері берілген
(9.82) теңдеулер жүйесіне қойып,
шамасына қысқартқаннан кейін,
-тің
бірдей дәрежелері коэффициенттерін
теңестіру арқылы анықталады. Мысалы
М.34.
теңдеулер
жүйесін шешейік.
Шешуі.
Сипаттаушы
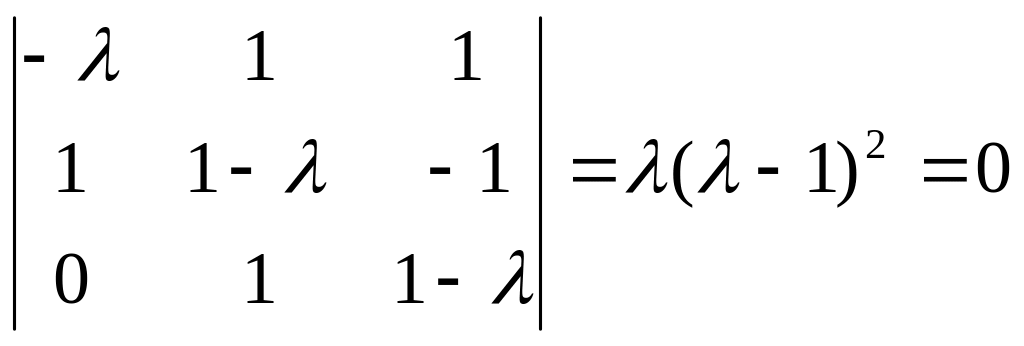теңдеуінің
және екі еселі
түбірлері бар. Мұндағы
түбірге
меншік векторы және
шешімі сәйкес келеді.
Ал
екі еселі
түбірге (9.88) шешімге сәйкес
векторлық түрдегі немесе
координаттық түрдегі шешімді аламыз.
Мұндағы
сандарын анықтауымыз қажет. Осы шешімдерді
берілген теңдеулер жүйесіне қойып,
шамасына қысқартқаннан кейін, белгісіз
коэффициенттерін анықтайтын (9.92)
теңдеулер
Мұндағы
ерікті тұрақтылар. Содықтан да, оларды
түрінде алып,
меншік санға сәйкес шешімдерді аламыз
Енді алғашқы шешіммен біріктіру арқылы, берілген теңдеулер жүйесінің жалпы шешімін
түрінде аламыз.
Ескерту.
Коэффициенттері тұрақты біртекті емес
сызықты дифференциалдық теңдеулер
жүйесінің
жалпы шешімін алу үшін, сәйкес біртекті
теңдеулерінің іргелі шешімдер жүйесін
пайдаланамыз. Мұндағы
тұрақты коэффициенттерден құралған
матрица,
теңдеулер жүйесінің оң жағындағы
вектор-функция.
М.35.
Коши есебін
шешейік.
Шешуі.
Алдымен берілген біртекті емес теңдеулер
жүйесіне сәйкес біртекті теңдеулер
жүйесінің іргелі шешімдер жүйесін
табамыз, яғни
болғандықтан,
()
Бұл
теңдеулер жүйесіне сәйкес сипаттаушы
теңдеудің түбірлері
.
Өз кезегінде, меншік векторлар
түрін қабылдайды. Демек, біртекті
()теңдеудің
жалпы шешімін
түрінде жазамыз. Мұндағы
-тен
тәуелді функциялар болса, берілген
әртекті теңдеулер жүйесінің жалпы
шешімін
()
түрінде іздейміз. Онда сәйкес туындылар,
болғандықтан, берілген біртекті емес теңдеулер жүйесіндегі орындарына қойып, түрлендіру арқылы
теңдігін аламыз.
Демек, берілген теңдеудің жалпы шешімі
түрін
қабылдайды. Енді берілген
бастапқы шарттарды қолданып,
және
болатындығын көреміз.
Сонымен, берілген Коши есебінің шешімі
Есептер мен жаттығулар
1.
Изоклин тәсілін пайдаланып,
дифференциалдық
теңдеуінің интегралдық қисықтарын
тұрғызыңыз.
2. Әрбір нүктедегі жанаманың бұрыштық коэффициенті жанасу нүктесінің абсциссасына пропорционал болатын қисықтың парабола екендігін көрсетіңіз.
3. Төмендегі бірінші ретті дифференциалдық теңдеулерді және Коши есептерін шешіңіз
à
á)
â)
ã)
ä)
(Жауабы
а)
ә)
б)
в)
г)
д)
).
4.
Төмендегі дифференциалдық теңдеулерді
және Коши есептерін шешіңіз
а)
ә)
б)
в)
г)
д)
ж)
з)
(Жауабы
а)
ә)
б)
в)
г)
д)
ж)
з)
)
5. Төмендегі теңдеулер жүйелерінің жалпы шешімдерін табыңыз
а)
ә)
(Жауабыа)
ә)
).