Шешуі. Ол үшін берілген функциялардан құрылған Вронскианның нөлден ерекше болатындығын көрсетсек жеткілікті (9.6-9.7 теоремалар). Шынында да,

Cебебі әртүрлі сандары үшін Вандермонд^) анықтауышы деп аталатын,

(9.59)

болады.

§ 9.5. Коэффициенттері тұрақты сызықты

дифференциалдық теңдеулер

1. Біртекті сызықты дифференциалдық теңдеулер. Сипаттаушы теңдеу. Мына (9.60)

теңдеу, мұндағы  тұрақты нақты сандар, коэффициенттері тұрақты біртекті сызықты дифференциалдық теңдеу деп аталады. Жоғарыдағы дифференциалдық операторды пайдаланып, (9.60) теңдеуді қысқаша түрінде жазуға болады.

Бұл (9.60) теңдеудің шешімін Эйлер тәсілі бойынша

(9.61)

түрінде іздейміз. Демек, берілген теңдеу

түрін қабылдайды. Мұндағы . Ендеше,

(9.62)

теңдігі берілген (9.60)  біртекті сызықты дифференциалды теңдеуге сәйкес сипаттаушы теңдеу, ал

(9.63)

сипаттаушы көпмүшелік деп аталады.

Сонымен, теңдеудің (9.61) шешіміндегі саны, (9.62) сипаттаушы теңдеудің шешімдері болғанда ғана, берілген (9.60) теңдеудің шешімі бола алады. Мысалы, теңдеуіне сәйкес сипаттаушы теңдеу түрін қабылдайды. Демек, сипаттаушы теңдеудің шешімі болатын әрбір үшін шешім сәйкес келетіндігін көреміз. Сондықтан да, (9.69) теңдеу шешімдерінің әртүрлі болатындығы белгілі, яғни оның шешімдері:

а)  нақты және әртүрлі;

б)  әртүрлі және олардың кейбіреулері еселі;

ә)  әртүрлі және кейбіреулері комплексті болып келеді.

Енді олардың әрбіреуіне жеке-жеке тоқталайық.

а) Айталық (9.62) сипаттаушы теңдеудің түбірлері әртүрлі және нақты болсын. Онда (9.60) теңдіктерінің біріншісі бойынша,

(9.64)

берілген (9.60) теңдеудің шешімдер жиынтығын аламыз.

Бұл алынған (9.64) функциялары сызықты тәуелсіз. Демек, олар берілген теңдеудің іргелі шешімдер жүйесі болып табылады. Онда жалпы шешім

(9.65)

түрін қабылдайды. Мұндағы  ерікті тұрақтылар.

М.25^. - үшінші ретті дифференциалды теңдеудің жалпы шешімін табайық.

Шешуі. Берілген теңдеуге сәйкес сипаттаушы теңдеу түрін, ал оның шешімдері: болады. Олар нақты және әртүрлі. Ендеше, ізделініп отырған жалпы шешім  болады.

б) Айталық, (9.62) сипаттаушы теңдеудің түбірлерінің кейбіреуі (мысал үшін ) еселі болсын. Онда болады. Бұл  еселі түбірге шешімі сәйкес келеді. Ал қалған іргелі шешімдер жүйесін құрайтын шешім үшін функциялары алынады.

Егерде  еселі, қалған әртүрлі және нақты сандар болса, онда (9.60) теңдеудің жалпы шешімі,

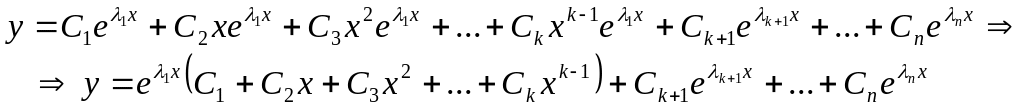(9.66)

түрін қабылдайды.

Мысалы, 7-ші ретті дифференциалдық теңдеуге сәйкес келетін сипаттаушы теңдеу түбірлері: болсын. Онда ол теңдеудің шешімін (9.66) теңдік бойынша жазамыз 

ә) Айталық сипаттаушы теңдеу түбірлерінің ішінде комплекстілері де кездесетін болсын, яғни Ал берілген теңдеудің коэффициенттері нақты сандар болғандықтан, комплекс түбірдің түйіндесі де сипаттаушы теңдеудің түбірі болады. Ал (9.61) теңдік бойынша,

(9.67)

берілген (9.60) теңдеудің шешімі болып табылады.

Дәл осы сияқты саны үшін функциясы да (9.60) теңдеудің шешімі бола алады. Өз кезегінде, (9.67) теңдіктегі функциялары (9.60) теңдеуінің сызықты тәуелсіз және олар осы теңдеудің нақты шешімдері болады.

Сонымен, берілген теңдеудің шешімі болып табылады.

М.26^.  дифференциалдық теңдеуді шешейік.

Шешуі. Берілген теңдеуге сәйкес сипаттаушы теңдеу  түрін қабылдайды. Ал оның түбірлері болады. Онда (9.61) теңдіктердің біріншісі бойынша: берілген теңдеудің шешімдерi. Ендеше, оның жалпы шешімі, түрінде жазылады.

Ескерту. Егер, (9.71) теңдеудің еселі комплекс түбірі болса, онда (9.71) дифференциалдық теңдеудің комплекс мәнді шешімі болып табылады. Ал бұл кезде жалпы шешім,

(9.68)

түрін қабылдайды.

Мысалы, берілген дифференциалдық теңдеуге сәйкес сипаттаушы теңдеудің түбірлері  болсын. Онда теңдеудің шешімі 

.

2. Біртекті емес сызықты дифференциалды теңдеулер. Коэффициенттері тұрақты біртекті емес сызықты дифференциалды теңдеу

(9.69)

түрінде беріледі. Жоғарыдағы 9.8-теорема бойынша (9.65) теңдеудің шешімін

(9.70)

екі шешімнің қосындысы түрінде іздейміз. Оның біріншісі  берілген (9.80) біртекті емес теңдеудің кез келген бір дербес шешімі, ал екіншісі  (9.69) сәйкес келетін  біртекті теңдеудің жалпы шешімі, яғни іргелі шешімдер жүйесі. Ендеше, берілген (9.69) теңдеу шешімдерінің екіншісі жоғарыдағы пунктте толық келтірілді. Сондықтан да, барлық жұмыс (9.70) теңдіктің біріншісін табуға келіп тіреледі. Енді осының әртүрлі шараларына тоқталайық.

Берілген (9.69) біртекті емес дифференциалдық теңдеудің дербес шешімін табу негізінен, оның оң жағындағы функциясының түріне негізделіп алынады. Демек, дербес шешім табу жәй амалдар қолдану арқылы сызықты алгебралық теңдеулер жүйесін дифференциалдау мен шешуге келіп тіреледі. Бұл тәсіл дербес шешімді сұрыптау немесе анықталмаған коэффициенттер тәсілі деп аталады.

Сонымен, (9.69) теңдеудің оң жағындағы функция жалпы

, (9.71)

мұндағы  коэффециенттері тұрақты және нақты, сәйкес -және -дәрежелі көпмүшеліктер түрінде алынады. Енді оның дербес жағдайларын қарастырамыз.

1^°. Айталық,

, (9.72)

, түрінде берілген болсын. Онда дербес шешім

, (9.73)

мұндағы  әзірге белгісіз коэффициенттер түрінде ізделеді. Осы шешімде сәйкес туындыларын табу арқылы (9.69) теңдеудегі орнына қояйық 

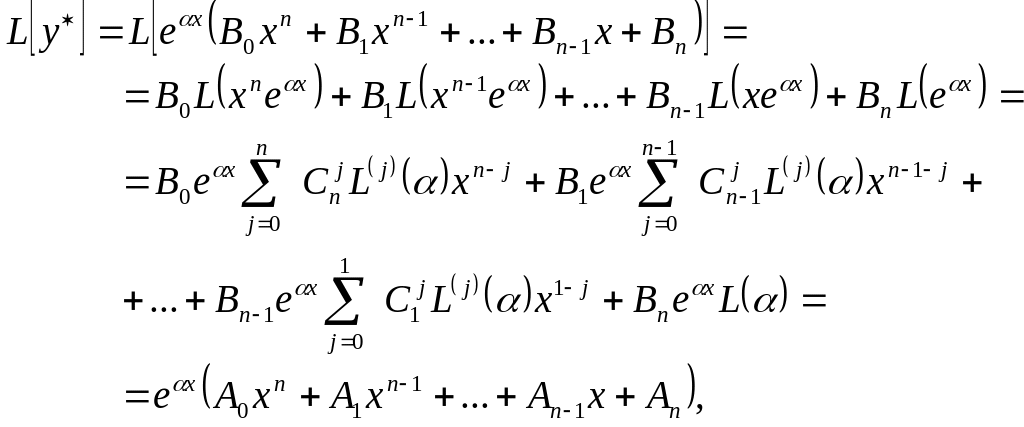(1)

мұндағы  биномиалдық коэффициенттер. Бұл (1) теңдіктің екі жағында шамасына қысқартып, қосындыларды жіктеп жазу арқылы

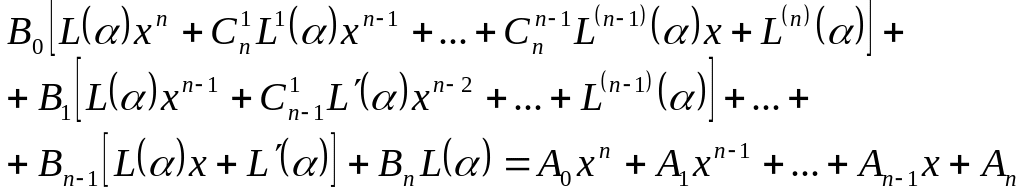(2)

теңдігін аламыз. Бұл теңдіктің екі жағында дәрежелері бірдей -ретті көпмүшеліктер. Ендеше, олардағы айнымалы -тің бірдей дәрежелерінің коэффициенттерін теңестірсек,

(3)

алгебралық теңдеулер жүйесін аламыз.

а) Егер  (9.69) теңдеудің сол жағындағы біртекті теңдеуге сәйкес сипаттаушы теңдеудің түбірі болмаса, онда біртіндеп (3) теңдеулер жүйесіндегі коэффициентттерін табамыз, және ол тек жалғыз түрде ғана

(4)

табылады.

Сонымен, , сипаттаушы теңдеудің түбірі болмаса, онда оң жағы (9.71) түрде болатын (9.69) дифференциалдық теңдеудің дербес шешімі (9.72) түрде ізделеді.

ә) Енді теңдеуінің еселі түбірі болса, онда

(5)

теңдіктері орындалады. Бұл кезде (9.69) теңдеудің шешімі

(9.74)

түрінде ізделінеді.

Шынында да, (9.84) өрнегін (9.80) теңдеуге қойсақ, шамасына қысқартқаннан кейін

(6)

теңдігі шығады.

Енді, әдеттегідей, (6) теңдіктің екі жағындағы -тің бірдей дәрежелерінің коэффициенттерін теңестіру арқылы,

(7)

алгебралық теңдеулер жүйесін аламыз. Бұдан біртіндеп коэффициенттері табылады.

Сонымен, егер сипаттаушы теңдеудің еселі түбірі болса, онда оң жағы (9.71) түрде болатын, (9.69) дифференциалдық теңдеудің дербес шешімі (9.73) түрде ізделінеді.

Енді (9.69) теңдеудің оң жағы болғанда,

(9.75)

түрінде берілген болсын. Бұл кезде екі жағдайды ескереміз.

а)  теңдеуінің түбірі болмаса, онда берілген теңдеудің дербес шешімін

(9.76)

түрінде іздеу керек.

ә) Егерде  теңдеуінің еселі түбірі болса, онда берілген дифференциалдық теңдеудің дербес шешімін

(9.77)

түрінде іздейміз.

М.27^*. теңдеуін шешейік.

Шешуі. Сәйкес сипаттаушы теңдеуінің түбірлері яғни екі еселі түбір. Демек, берілген біртекті емес теңдеуге сәйкес біртекті  теңдеуінің жалпы шешімі (9.75) бойынша

(^*)

болады.

Берілген теңдеудің оң жағы  екінші дәрежелі көпмүшелік және  сипаттаушы теңдеудің екі еселі түбірі болғандықтан, берілген дифференциалдық теңдеудің дербес шешімін (9.7)

(^**)

түрінде іздейміз. Сәйкес туындыларды тауып, берілген теңдеудегі -тің орындарына қойсақ,

болғандықтан, теңдігін аламыз. Енді (7) теңдеулер жүйесін құрамыз.

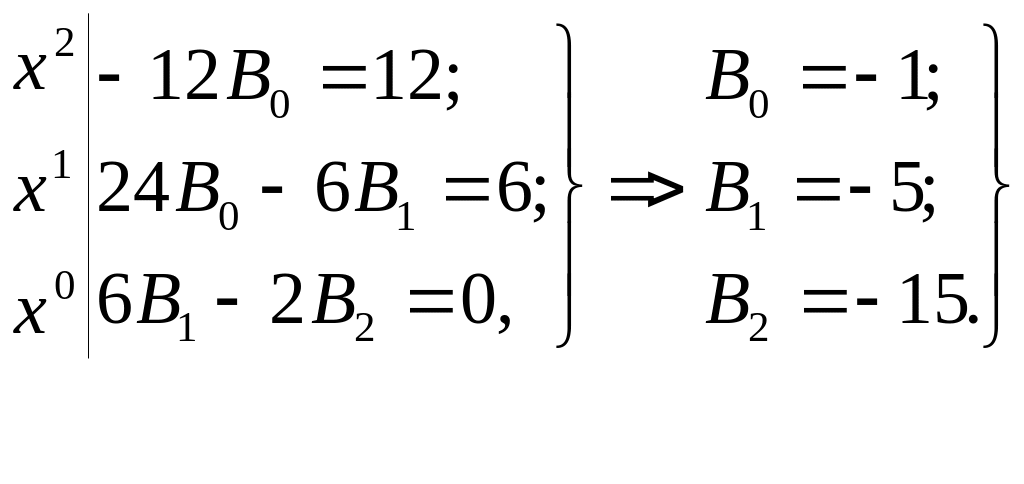
Табылған коэффициенттерін (^**) теңдікке апарып қойсақ, берілген дифференциалдық теңдеудің дербес шешімі түрін қабылдайды. Ал берілген теңдеудің жалпы шешімі, (9.65) бойынша (^*) және (^**) шамаларын біріктіру арқылы,

түрінде алынады.

М.28*. дифференциалды теңдеуін, бастапқы шарттарды қанағаттандыратындай етіп, Коши есебін шешейік.

Шешуі. Алдымен сипаттаушы теңдеуін шешеміз. Оның түбірлері болады. Онда сәйкес біртекті теңдеудің жалпы шешімі (9.65) бойынша,

(^*)

түрін қабылдайды.

Берілген теңдеудің оң жағы болғандықтан, және ол сипаттаушы теңдеудің түбірі емес. Онда берілген біртекті емес теңдеудің дербес шешімін (9.73) бойынша,

(^**)

түрінде іздейміз. Демек,

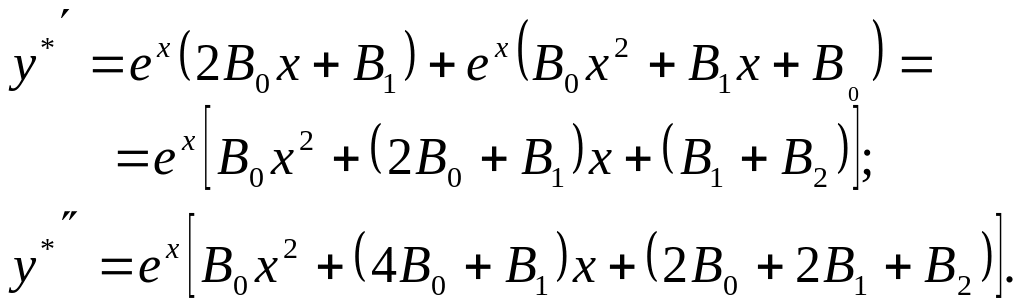
Алынған шешім мен оның туындыларын орындарына қою арқылы және болғандықтан, оған қысқартсақ,

Онда сәйкес (3) теңдеулер жүйесін құру арқылы :

белгісіз коэффициенттердің мәндерін табамыз. Демек, іздеп отырған дербес шешім түрін қабылдайды да, берілген теңдеудің жалпы шешімі  (^*), (^**) теңдіктерді біріктіру арқылы

Енді берілген бастапқы (әуелгі) шарттарды пайдаланып, Коши есебін шешуге кірісеміз. Ол үшін,

2^°. Берілген (9.69) дифференциалдық теңдеудің оң жағындағы функция,

(9.78)

түрін қабылдайтын болсын. Мұндағы функцияларын Эйлер формулаларын 

(9.79)

пайдаланып, (9.79) теңдікті түрлендіретін болсақ,

(^*)

түрін қабылдайды. Демек, берілген (9.69) теңдеудің оң жағындағы функция екі қосылғыштан тұрады, яғни

(^**)

Мұндағы — дәрежелі түйіндес көпмүшеліктер. Бұдан функцияларының да (9.72) түрге көшетіндігін көреміз. Онда суперпозициялау (қосақтау) принципі бойынша, берілген біртекті емес теңдеудің дербес шешімін қосынды, яғни түрінде іздейміз және сәйкес

  біртекті емес теңдеулер шешімдері болатындығын аңғарамыз.

Енді болғандықтан, теңдігі орындалатындығын көрсетейік. Шынында да, теңдігінен, туындайды (сызықшалар түйіндес комплекс өрнектер деген ұғымды білдіреді). Ал  нақты коэффициентті оператор болғандықтан, теңдігі шығады. Ендеше, яғни егер  теңдеуінің шешімі болса, онда  теңдеуінің дербес шешімі болып шығады.

Ал теңдеулерін шешу жолдары 1^°- бөлікте көрсетілген.

Ендігі жерде, шамаларының сипаттаушы теңдеудің комплекс түбірлері арасындағы байланысты көрсетейік.

а) Айталық  сипаттаушы теңдеудің түбірлері болмасын. Онда теңдеулерінің дербес шешімдерін түрлерінде іздеуміз керек. Мұндағы  түйіндес, коэффициенттері нақты, әзірге белгісіз дәрежелі көпмүшеліктер. Сонымен, теңдеуінің шешімі (^**)

түрін қабылдайды. Мұндағы комплексті дәрежелі көпмүшеліктің нақты және жорамал бөліктері. Оларды, сәйкес деп белгілесек (^**) теңдіктен,

(9.80)

берілген (9.89) теңдеудің ізделініп отырған дербес шешімін аламыз.

Сонымен, берілген (9.80) біртекті емес дифференциалды теңдеудің оң жағындағы функция (9.98) түрде ал — сәйкес сипаттаушы теңдеуінің түбірі болмаған жағдайда, теңдеудің дербес шешімі (9.100) түрде ізделінеді, мұндағы .

ә) Егер — сипаттаушы теңдеудің еселі комплекс түбірі болса, онда, 1^°- бөлік сияқты, берілген (9.89) теңдеудің оң жағы (9.91) түрде болғанда, оның дербес шешімі

(9.81)

түрінде ізделінеді. Мұндағы  коэффициенттері әзірге белгісіз дәрежелі көпмүшеліктер.

М.29^*. теңдеуін шешейік.

Шешуі. Сипаттаушы , онда сәйкес біртекті теңдеуінің жалпы шешімі түрін қабылдайды. Енді берілген теңдеудің оң жағының түріне байланысты, санын құрсақ, ол сан сәйкес сипаттаушы теңдеудің түбірі емес. Ендеше, жоғарыдағы кестенің үшінші бөлімінің бірінші бабы бойынша берілген теңдеу. Сонымен, коэффициенттері тұрақты біртекті емес сызықты дифференциалдық теңдеудің оң жағындағы функциясының жоғарыда келтірілген түрлеріне байланысты, оның дербес шешімдері үшін төмендегідей кесте құруға болады.

Ескерту. Көпшілік жағдайда біртекті емес дифференциалдық теңдеудің оң жағындағы функциясы кестеде берілген түрлердің қосындысы болып келеді. Бұл кезде сәйкес дербес шешімді, шешімдерді біріктіру арқылы табамыз.

Дербес шешімін, болғандықтан, сәйкес туындыларымен

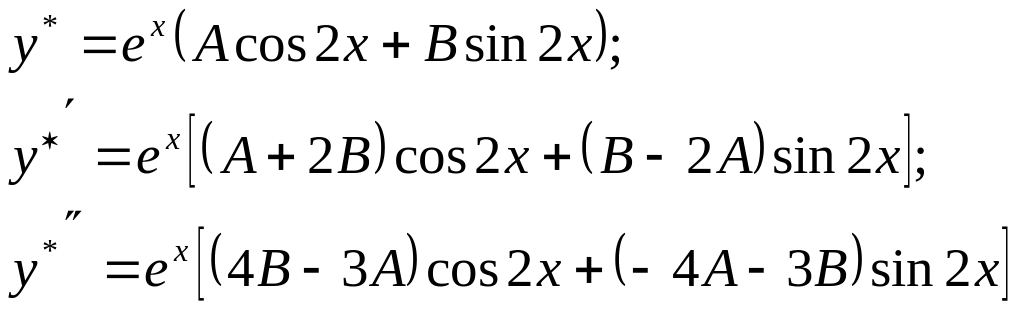
түрінде іздейміз. Алынған шешімді орнына қойып, шамасына қысқартсақ,

теңдігі шығады. Енді бұл теңдіктің екі жағындағы пен өрнектерінің сәйкес коэффициенттерін теңестірсек:

белгісіз коэффициенттер және мәндерін табамыз. Демек, дербес шешім болады да, берілген біртекті емес теңдеудің жалпы шешімі болады.

M.30^*.

теңдеуге сәйкес дербес шешімнің түрін көрсетейік.

Шешуі. Ол үшін алдымен сәйкес сипаттаушы теңдеудің түбірлерін табайық 

Берілген теңдеудің оң жағындағы мұндағы Демек,  сипаттаушы теңдеудің еселі түбірі, ал  яғни Ендеше, берілген біртекті емес дифференциалдық теңдеудің дербес шешімін

түрінде іздейміз.

2- кесте

Рет нө-мірi		Сипаттаушы – теңдеудің түбірлері	Дербес шешімнің – түрлері
		 сипаттаушы тең-деудің түбірі емес
		 сипаттаушы тең-деудің еселі түбірі
		сипаттаушы тең-деудің түбірі емес
		сипаттаушы тең-деудің еселі түбірі
		 сипаттаушы теңдеудің түбірі емес
		 сипаттаушы теңдеудің еселі түбірі

М.31^. теңдеуі үшін дербес шешім түрін көрсетейік.

Шешуі. Сипаттаушы теңдеу түбірлері  . Ал  үш функцияның қосындысы. Онда болғандықтан, берілген теңдеудің дербес шешімі үш шешімді біріктіруден шығады. Демек, . Мұндағы, .

4-ДӘРІС