§ 9.4. Жоғарғы ретті сызықты дифференциалдық

теңдеулер

1. Жалпы түсініктер. Төмендегі

(9.53)

түрінде жазылған теңдеу, -ретті біртекті емес (әртекті), ал болса, яғни

(9.54)

-ретті біртекті сызықты дифференциалдық теңдеу деп аталады. Мұндағы  кесіндісінде берілген үзіліссіз функциялар. Бұл (9.53) немесе (9.54) теңдеулерінің сол жақтарында тұрған

(9.55)

өрнегі -ретті дифференциалдық оператор деп аталады.

Дифференциалдық операторлар төмендегі екі қасиетке

1^.  оператордың біртектілігіне

2^.  оператордың аддивтивтілігіне сүйенеді және олар сызықты операторлар деп аталады.

Сызықты операторларды ескере отырып, (9.53), (9.54) теңдеулерді,

(9.53^)

(9.54^)

түрінде жазуға болады.

Айталық, (9.54) және (9.54^) біртекті сызықты дифференциалдық теңдеуі беріліп,  осы теңдеудің шешімдері болса, ол төмендегі қасиеттерге сүйенеді 

1^. қосындысы да (9.54) (немесе (9.54^)) теңдеуінің шешімі болады 

2^. Кез келген тұрақтысы үшін, (немесе ) көбейтіндісі де осы теңдеудің шешімі болады 

3^. Егерде және  (9.53) (немесе (9.53^)) біртекті емес теңдеулердің шешімдері болса, онда олардың айырымы , сәйкес  біртекті теңдеудің шешімі болады 

4^. Егер  комплекс мәнді функция біртекті (9.54) (немесе (9.54^)) теңдеудің шешімі болса, онда оның нақты және жорамал бөліктері болатын , функциялары әрқайсысы жеке-жеке берілген теңдеудің шешімдері болады.

2. Сызықты тәуелсіз функциялар. Вронскиан. Егер бәрі бірдей қатарынан нөлге тең болмайтын нақты сандары табылып, функциялары үшін,

(9.56)

тепе-теңдігі орындалатын болса, онда функциялары аралығында сызықты тәуелді, ал (9.56) тепе-теңдік тек қана болғанда ғана орындалатын болса, онда аралығында функциялары сызықты тәуелсіз деп аталады.

9.5. Теорема. Егер аралығында функциялары өзара сызықты тәуелді және осы аралықта берілген функциялардың -ретті туындылары бар болса, онда үшін

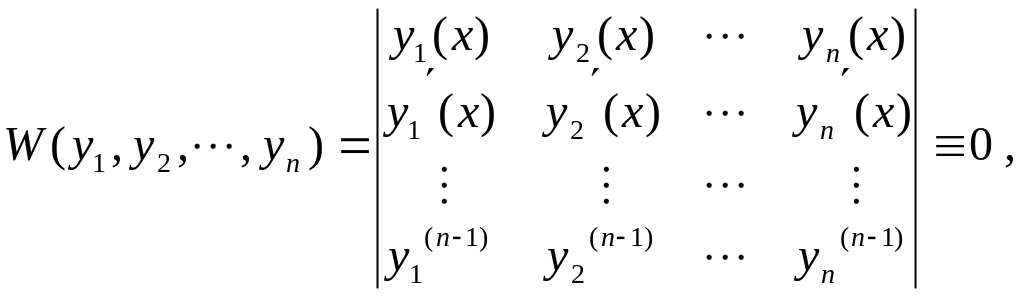(9.57)

теңдігі орындалады. Бұл алынған (9.57)  Вронский^) анықтауышы немесе Вронскиан деп аталады.

Дәлелдеуі. Теореманың шарты бойынша өзара сызықты тәуелді. Онда олардың кез келген біреуі, мысал үшін , қалғандарының сызықты комбинациясы болады, яғни сандары табылып,

(9.58)

теңдігі орындалады. Онда бұл функциялардың вронскианы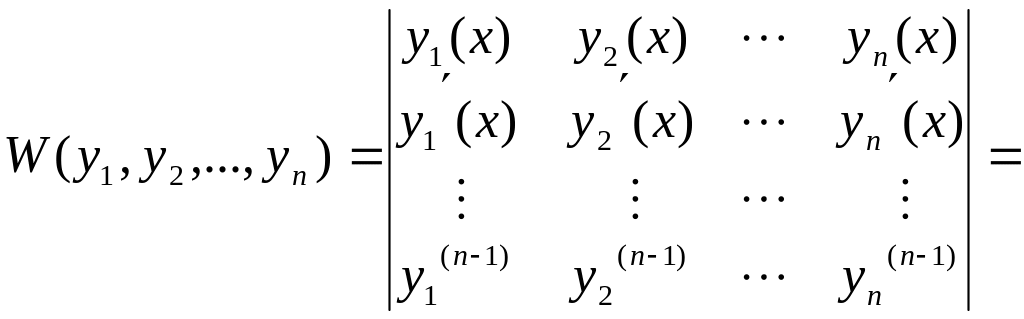

Себебі, бұл тепе-теңдіктегі соңғы баған қалған бағандардың сызықты комбинациясын құрайды.

9.6. Теорема. Коэффициенттері аралығында үзіліссіз болатын  біртекті сызықты дифференциалдық теңдеудің шешімдері болатын функцияларының өзара сызықты тәуелсіз болуы үшін, вронскианның болуы, қажетті және жеткілікті.

Ескерту. Егер функциялары және олардың алғашқы -ретті туындыларын нүктесі үшін есептейтін болсақ, онда сәйкес нүктесіндегі вронскиан

санымен анықталады.

9.7. Теорема. Айталық,  теңдеуінің интервалындағы шешімдері болсын. Онда:

1^. Егер вронскианы интервалында жататын ең болмағанда бір нүктесінде нөлден ерекше болса, онда интервалында сызықты тәуелсіз;

………………………………………………………………..

^)Ю.Гене - Вронский (1776-1853)  польша математигі.

2^. Егер аралығында жататын нүктесі табылып, сол нүктеде Вронскиан нөлге тең, яғни болса, онда шешімдері сызықты тәуелді және үшін болады.

М.23^. Егер  әртүрлі сандар болса, онда функцияларының кез келген аралығында сызықты тәуелсіз болатындығын көрсетейік.