§ 9.3. Жоғарғы ретті дифференциалдық теңдеулер

1. Жалпы түсінік. Коши есебі. Төменде келтірілген

, (9.1)

немесе ең жоғарғы туындысы арқылы шешілген

(9.2)

теңдеулері -ретті дифференциалдық теңдеу деп аталады. Бұл теңдеулердің Оху жазықтығындағы шешімі

үшін (9.40)

функциясымен анықталады. Ал –ретті дифференциалдық теңдеулердің жалпы шешімі  ерікті интегралдық тұрақтыдан тәуелді, яғни

(9.41)

рет үзіліссіз дифференциалданатын функция болып табылады. Демек, (9.1) немесе (9.2) дифференциалдық теңдеудің жалпы интегралы, бірінші ретті теңдеу сияқты,

(9.42)

теңдігімен анықталады.

Геометриялық тұрғыдан, берілген -ретті дифференциалдық теңдеудің жалпы шешімі (интегралы) Оху жазықтығында жатқан  тұрақтылардан тәуелді қисықтар жиынтығы болады. Ал олардың ішінен біреуін бөліп алу, оның дербес шешімін осы тұрақтыларды анықтайтын теңдеулерден басқа, қосымша шарттар берілуі қажет. Ондай шарт ретінде (9.40) функциясының және оның ( )-ретті туындыларының аралығында жататын нүктесіндегі мәндері

(9.43)

алынады. Берілген (9.43) теңдіктер бастапқы шарттар немесе Коши шарттары деп аталады. Ал оларды пайдалану арқылы (9.1) немесе (9.2) теңдеудің дербес шешімін (интегралын) табу Коши есебін шешу (интегралдау) деп аталады.

Айталық, (9.1) немесе (9.2) дифференциалдық теңдеу және (9.43) бастапқы шарттар берілген болсын.

9.4. Теорема (Коши есебі шешімінің бар және оның жалғыз болуы жөнінде). Егер функциясы нүктесінің белгілі бір маңайында үзіліссіз және үзіліссіз дербес туындылары болса, онда дифференциалдық теңдеудің нұкте маңайында анықталған және (9.43) бастапқы шарттарды қанағаттандыратын шешімі бар және ол шешім жалғыз болады.

2. Ретін төмендетуге болатын теңдеулер. Негізгі тәсіл  теңдеудің ретін төмендету. Осы тәсілдердің кейбіреулеріне тоқталайық.

1^. Айталық, (9.1) -ретті теңдеудің оң жағындағы функция тек тәуелсіз айнымалы тен ғана тәуелді, яғни

(9.44)

түрін қабылдайтын болсын. Бұл теңдеудің ретін төмендету тізбектеп интегралдау арқылы жүзеге асырылады. Демек,

(9.45)

М.14^. теңдеуін шешейік.

Шешуі. Алынған (9.45) теңдеулер жүйесі бойынша, берілген дифференциалдық теңдеу біртіндеп интегралданады

оның жалпы шешімін аламыз.

Ескерту. Берілген (9.44) теңдеуді интегралдау функциясының -ретті алғашқы функциясын табу мен пара-пар. Ендеше, оның алғашқы функциясы

(9.46)

теңдігімен анықталады. Мұндағы . Онда жоғарыдағы^- мысалдағы функцияның алғашқы функциясы

.

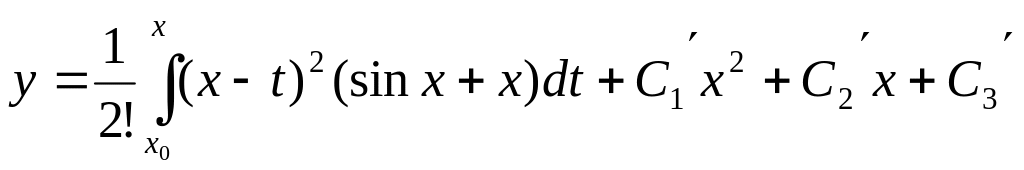2^. Берілген -ретті дифференциалды теңдеудің құрамында ізделіп отырған функциясы мен оның -ретті туындысын қоса алғандағы алғашқы ретті туындылары енбейтін болсын, яғни

. (9.47)

Бұл теңдеуді шешу үшін жаңа  әзірге белгісіз функциясын,

(9.48)

түрде енгіземіз. Онда берілген (9.47) теңдеу түрге көшеді. Оны шешу арқылы  дифференциалдық теңдеудің жоғарыда қарастырылған (9.44) түрін аламыз.

М.15^.  теңдеудің жалпы шешімін табайық.

Шешуі. Берілген теңдеу 2^-топқа жатады, мұндағы . Демек, . Онда берілген теңдеу,

сызықты дифференциалдық теңдеуге айналады. Ендеше,

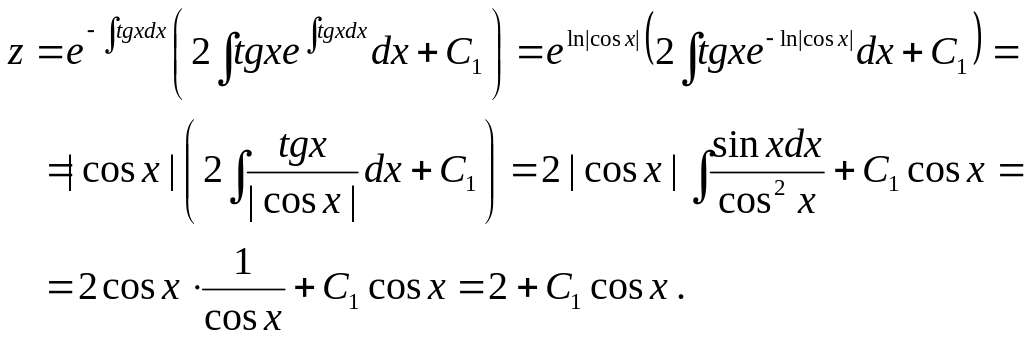
Өз кезегінде болғандықтан, (9.45) теңдіктерді қолдану арқылы

3^. Айталық, берілген жоғарғы ретті теңдеудің бұл түріне тәуелсіз айнымалы қатыспайтын болса,

(9.49)

Бұл теңдеуге ауыстыруын жасасақ, оның реті бірге төмендей-тіндігін көреміз. Шынында да,

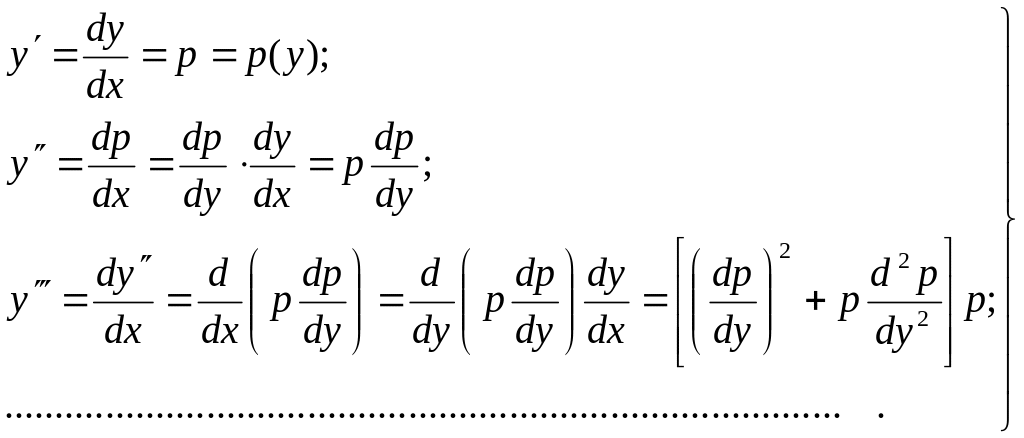(9.50)

Жоғарыдағы (9.50) теңдіктердің оң жағында жаңадан енгізілген функциясы туындыларының реті, сол жағындағы функциясы туындыларымен салыстырғанда бірге кем. Демек, оларды берілген (9.45) теңдеудегі орындарына қойсақ,

(9.51)

тен тәуелді функциясы бойынша -ретті дифференциалдық теңдеу аламыз. Айталық,  аралығында нөлден ерекше, (9.51) теңдеудің шешімі болып, ол болғандықтан,

(9.52)

айқындалмаған түрдегі берілген (9.49) теңдеудің шешімін аламыз.Ал көпшілік жағдайда, (9.51) теңдеудің реті болғандықтан, үшін  интегралдық тұрақтыдан тәуелді функциялар жиынтығын аламыз. Өз кезегінде, оған  ерікті тұрақты-лардан тәуелді, берілген (9.49) дифференциалдық теңдеудің жалпы шешімі сәйкес келеді.

М.21^.  дифференциалдық теңдеуін шешейік.

Шешуі. Берілген теңдеуге тәуелсіз айнымалы қатыспайды. Демек, жоғарғы ретті дифференциалдық теңдеудің 3^-топқа жатады. Ендеше,

.

Онда берілген теңдеу

Егер  а)

ә)

Бұл кезде , немесе  берілген теңдеудің жалпы интегралын аламыз.

М.22^.  Коши есебін шешейік.

Шешуі. Жоғарыдағы мысал сияқты, болғандықтан, . Бұдан  а)  бірақ бұл шешім берілген бастапқы шарттарды қанағаттандырмайды 

ә) .

Енді бастапқы шарттарды пайдалану арқылы,

Ендеше, болғандықтан, .

Сонымен, берілген Коши есебінің шешімі функциясы болып табылады.

3-ДӘРІС