IX. Жәй дифференциалдық теңдеулер
I-ДӘРІС
§ 9.1. Жәй дифференциалдық теңдеулер
1. Дифференциалдық теңдеулерге келтірілетін есептер.
1. Әрбір нүктесіне жүргізілген жанама мен Ох өсі арасындағы бұрыштың тангенсі жанасу нүктесі ординатасына пропорционал болатын қисықтың теңдеуін табайық.
Шешуі.
Айталық,
ізделініп отырған қисықтың теңдеуі
болсын. Функция туындысы (§5.1) анықтамасын
еске алсақ, ізделініп отырған қисықтың
бойында жатқан
нүктесіне жүргізілген жанама мен Ох
өсі
арасындағы
бұрыштың тангенсі
болатындығы белгілі. Ендеше, берілген
есептің шартын пайдаланып,
(1)
теңдігін
аламыз. Мұндағы
пропорционалдық коэффициент. Алынған
теңдікке, ізделіп отырған
функциясы мен осы функцияның туындысы
қатысатынын көреміз. Осы
теңдік дифференциалдық
теңдеу
деп аталады. (1) теңдікті түрлендіріп
интегралдау арқылы
(2)
ізделіп отырған функцияны аламыз.
2.
Tұтқыр ортаға бастапқы
жылдамдықпен массасы
болатын дене бататын болсын. Ортаның
кедергісі дене қозғалысы жылдамдығына
пропорционал (
пропорционалдық
коэффициент) болғандағы дененің қозғалу
заңдылығын анықтайық (9.1-
сурет)
.
Шешуі.
Айталық,
қозғалысы
уақыттан
тәуелді
дененің
өсінен қашықтау аралығы болсын. Онда
дене
қозғалысының сәйкес жылдамдығы мен
үдеуі болады. Ендеше,
Ньютонның екінші заңы бойынша
,
(3)
мұндағы
.
Осы алынған (4) теңдік дене қозғалысының
ізделіп отырған
функциясы мен оның
туындыларын байланыстыратын дифференциалдық
теңдеу болып табылады.
Енді
дене қозғалысының
заңдылығын бастапқы
уақытта
және
жылдамдығы
болатындай етіп табамыз. Ол үшін соңғы
алынған (3) дифференциалдық теңдеудің
екі жағын да
шамасына көбейтіп түрлендіреміз де,
интегралдау арқылы жылдамдықты табамыз.
Сонымен,
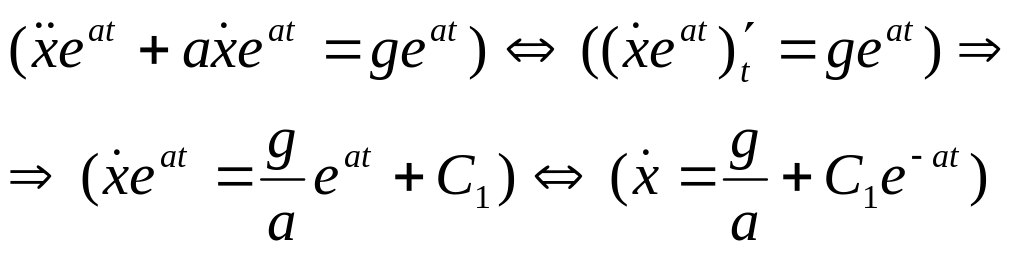(4)
мұндағы
интегралдық ерікті тұрақты. Алынған
(3) дифференциалдық теңдеуді екінші рет
уақыт бойынша интегралдау арқылы, дене
қозғалысының заңдылығын аламыз
(5)
мұндағы
ерікті тұрақты сан. Алынған (4) қисықтар
жиынтығы (3) теңдеуді қанағаттандыратынына
оңай көз жеткізуге болады.
Ендігі
мақсатымыз, бастапқы
уақыттағы
және
шарттарын
қанағаттандыратын дене қозғалысы
заңдылығын анықтау. Ол үшін (4) және (5)
теңдіктерде
болса,
;
интегралдық тұрақтылар мәндерін аламыз.
Сонымен, ізделініп отырған дененің тұтқыр ортаға бату заңдылығы:
(6)
формуласымен анықталады.
2.
Дифференциалдық теңдеулер жөніндегі
түсінік.
Tәуелсіз
айнымалы
,
ізделінетін функция
және оның
туындыларын (ең болмағанда біреуінің
қатысуы) байланыстыратын,
(9.1)
теңдігі
ретті
(туындының
ең жоғарғы реті)
дифференциалдық
теңдеу
деп аталады.
Егер (9.1) дифференциалдық теңдеуді ең жоғарғы туындысы арқылы шешіп,
(9.2)
түрінде
жазсақ, ол қалыпты
дифференциалдық теңдеу деп
аталады. Алынған (9.1)
және (9.2)
теңдеулеріндегі
функциялары, сәйкес
ашық жиындарында анықталған.
Егер дифференциалдық теңдеулердегі ізделінетін функциясы бір айнымалыдан тәуелді болса жәй дифференциалдық теңдеулер, ал бірнеше айнымалылардан тәуелсіз болса дербес туындылы дифференциалдық теңдеу немесе математикалық физика теңдеуі деп аталады.
Ескерту. Aлдағы уақытта (егер ерекше атап өтпесек) тек жәй дифференциалдық теңдеулерді қарастырамыз.
Жоғарыдағы (1) және (3) дифференциалдық теңдеулерді шешу, яғни белгісіз функциясын табу кезінде оларды интегралдау арқылы жүзеге асырғанымыз белгілі. Ендеше, (9.1) дифференциалдық теңдеудің шешімі (немесе интегралы) деп:
а)
интервалында
рет дифференциалданатын нақты функциялар
класына жататын;
ә)
нүктесі;
б)
тепе-теңдігін қанағаттандыратын
интервалында анықталған
нақты функцияны айтады.
Мұндағы
функцияның анықталу
аймағы
деп аталады.
Осы
шарттарды қанағаттандыратын
функциясы (9.2)
дифференциялдық теңдеуді де
қанағаттандырады. Сондықтанда,
(9.1)-теңдеудің
шешіміне
сәйкес,
жазықтығында
жататын функция
графигі
берілген
дифференциалдық теңдеудің интегралдық
қисығы деп
аталады. Ал дифференциалдық теңдеудің
шешімін анықтау жолы, осы теңдеуді
интегралдау
деп аталады.
3.
Бірінші ретті дифференциалдық теңдеулер.
Коши есебі. Aйталық,
(9.1)
дифференциалдық теңдеудегі
=1,
яғни бірінші ретті дифференциалдық
теңдеу
(9.3)
берілген
болсын. Мұндағы
жиынында анықталған белгілі функция.
Немесе туындысы бойынша анықталған,
қалыпты дифференциалдық теңдеуді
(9.4)
қарастырайық.
Мұндағы
айнымалылары бойынша
жиынында анықталған белгілі функция.
Келтірілген (9.3)
теңдеуді
түрлендіру арқылы,
басқаша
(9.5)
бірінші
ретті дифференциалдық теңдеуді алуға
болады. Мұндағы
жиынында анықталған берілген функциялар.
Бірінші
ретті жәй дифференциалдық (9.3)
теңдеудің шешімі
(немесе
интегралы)
деп, а)
интервалында үзіліссіз дифференциалданатын
функциясы; ә)
үшін
нүктесі
функциясының анықталу аймағы болатын
ашық
жиынында жататын; б)
үшін
тепе-теңдігі орындалатын, (
)интервалында
анықталған
нақты
функцияны айтады.
Жоғарыдағы келтірілген 1 мысалдағыдай, (9.3) немесе (9.4) теңдеулердің сансыз көп шешімі (интегралы) болатындығы белгілі. Ал оның ішінен тек біреуін таңдап алу үшін қосымша алғы шарттар қойылады, яғни
(9.6)
бастапқы шарт деп аталады.
Сонымен, (9.3) немесе (9.4) дифференциалдық теңдеулердің (9.6) бастапқы шартты қанағаттандыратын шешімі дербес шешім, ал есеп Коши есебі деп аталады.
Берілген
(9.3)
немесе (9.4)
дифференциалдық теңдеулерге арналған
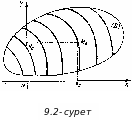
Коши есебінің геометриялық мағнасы,
олардың сансыз көп шешімдерінің ішінен
берілген
нүктесін басып өтетін интегралдық
қисықты бөліп алу (9.2-
сурет).
9.1.
Теорема (Коши
есебі шешімінің бар және оның жалқылығы
жөнінде).
Егер
функциясы
аймағында анықталған, үзіліссіз және
оның үзіліссіз дербеc
туындысы болса, онда
нүктесінің
-маңайы,
яғни
табылып, осы маңайда (9.4)
дифференциалдық теңдеудің
бастапқы
шартты
қанағаттандыратын
шешімі
бар
және ол
шешім
жалқы
болады.
М.1.
бірінші ретті дифференциалдық теңдеуді
шешейік.
Шешуі.
Aйталық
болсын. Онда
.
Мұндағы
интегралдық ерікті тұрақты. Берілген
теңдеуге сәйкес интегралдық қисықтар
Ох
өсі бойына орналасады және шешімнің
жалғыз болатындығы орындалмайды, себебі
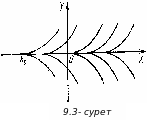
аралығындағы әрбір нүктеден
және
интегралдық қисықтары басып өтеді (9.3-
сурет).
Мұндағы
.
Себебі 9.1-теореманың жалғыздық шарты
орындалмайды
-да
Бірінші
ретті
дифференциалдық теңдеудің жалпы
шешімі
деп, біріншіден, кез келген
мәндері үшін
функциясы (9.4)
теңдеудің шешімі болып табылатын;
екіншіден, кез келген
бастапқы шарт үшін,
параметрін
тауып,
функциясы
шартын қанағаттандыратындай
параметрінен
тәуелді
біріне-бірі ұқсас функциялар жиынтығын
айтамыз
(9.3-сурет).
Ал бұл теңдеулердің дербес
шешімі
деп,
параметрінің
белгілі бір мәніне сәйкес жалпы шешімнен
бөлініп алынған
жалқы
шешімді айтады.
Демек, дербес шешім Коши есебінің шешімі
болып табылады.
Көпшілік
жағдайда,
теңдеуінің жалпы шешімінен
(9.7)
теңдігі
алынады және ол берілген дифференциалдық
теңдеудің жалпы
интегралы
деп аталады. Aл белгілі бір
үшін
алынған
оның дербес
интегралы
деп аталады. Бірінші ретті (9.3)
дифференциалдық теңдеудің әрбір
нүктесіндегі шешімнің жалғыздығы
бұзылатын, яғни әрбір
нүктесі аpқылы басқа да (9.3)
теңдеуінің шешімдері басып өтетін
болса, онда ол
ерекше шешім
деп аталады.