3. Неравномерное движение Задача

Автомобиль поехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 15 м/с. Найти среднюю скорость на всем пути. Показать, что средняя скорость меньше среднего арифметического значения скоростей V₁ и V₂.

По определению средней скорости:

Рассмотрим рис.

S/2 S/2

=10 м/с =15 м/с

На первой половине пути движение равномерное, поэтому:

S/2= V₁t₁ , t₁=

На второй половине пути движение также равномерное и поэтому:

S/2=V₂t₂, t₂=

Можем теперь записать:

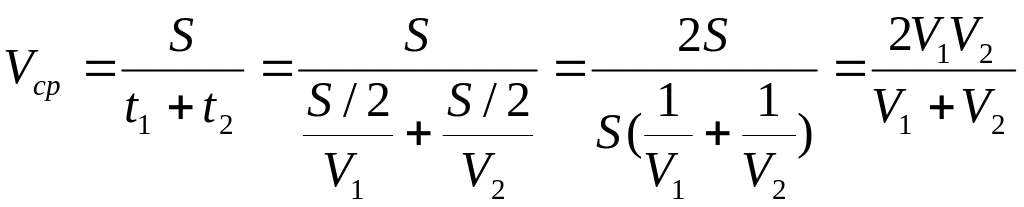
Докажем, что средняя арифметическая скорость больше средней скорости. Для этого рассмотрим знак их разности; если разность больше нуля, то это утверждение верно.

, т. к.

и

Средняя скорость меньше средней арифметической, т.к. большая часть времени автомобиль ехал с меньшей скоростью.

1. По графику зависимости координаты тела от времени ( рис.3) построить графики зависимостей ускорения, скорости и пути, пройденного телом, от времени. Начальная скорость равна нулю.

Рис. 3

2. Дан график зависимости скорости тела от времени (рис. 4). Построить графики зависимости пути и координаты от времени. Определить среднюю скорость за первые 2 и 5 с. Начальная координата равна нулю.

V(м/с)

3

0 2 4 6 t, c

-3

Рис. 4

3. Уравнения движения по шоссе велосипедиста, пешехода и бензовоза имеют вид : х₁= -0,4t² ; х₂= 400 - 0,6t и х₃= -300. Найти для каждого из тел: координату в момент начала наблюдения, проекции на ось х начальной скорости и ускорения, а также направление и вид движения.

4. Человек, стоящий на краю высохшего колодца, бросает вертикально вверх камень, сообщая ему скорость 10 м/с. Через какой промежуток времени камень упадет на дно колодца? Глубина колодца 15 м. Найти путь за 3 с. Определить скорость в 3-ю секунду. Построить графики зависимости y(t), S(t), V(t) , a(t).

5. Камень бросают с башни, сообщая ему начальную скорость, направленную вниз. 1) Какой она должна быть, чтобы камень за время 2 с опустился на 30 м? 2) Какой должна быть эта скорость, чтобы камень за 2 с опустился на 10 м ?

6. Свободно падающее тело за последнюю секунду падения прошло 1/3 своего пути. Найти время падения и высоту, с которой упало тело.

6. Свободно падающее тело прошло последние 30 м за время 0,5 с. Найти высоту падения.

8. Частица движется вдоль оси х так, что зависимость ее координаты от времени дается графиком, изображенным на рис. 5. Определить характер движения частицы и привести график зависимости пройденного ею пути от времени. Где оказывается частица в момент времени t₅?

Рис.5

9. Начальная скорость частицы , конечная - . Найти : а) приращение скорости , б) модуль приращения скорости , в) приращение модуля скорости .

9. Радиус-вектор частицы определяется выражением : . Вычислить: а) путь, пройденный частицей за первые 10 с движения, б) модуль перемещения за то же время.

3.11.Радиус-вектор частицы изменяется со временем по закону : .

Найти : а) скорость и ускорение частицы, б) модуль скорости в момент времени t=1с.

3.12.Частица движется со скоростью . Найти : а) перемещение частицы за первые 2 с ее движения; б) модуль скорости в момент времени t=2 с.

3.13.Частица движется со скоростью . Найти :

а) модуль скорости частицы в момент времени t=1 с;

б) ускорение частицы и его модуль;

в) путь, пройденный частицей с момента t₁=2 с до момента t₂=3 с.

3.14.Радиус-вектор частицы меняется со временем по закону , где -постоянный вектора, - положительная постоянная. Найти:

а) скорость частицы и ее ускорение в зависимости от времени;

б) промежуток времени, по истечение которого частица вернется в исходную точку, а также путь , который она пройдет за это время.

3.15.Радиус-вектор точки А относительно начала координат меняется со временем по закону где и - постоянные. Найти:

а) уравнение траектории точки у =у(x); изобразить ее график;

б) зависимость от времени скорости точки, ускорения и модулей этих величин;

в) зависимость от времени угла между векторами ускорения и скорости.

3.16.Точка движется в плоскости ху по закону , где и - положительные постоянные. Найти:

а) уравнение траектории точки у(x); изобразить ее график;

б) скорость и ускорение точки в зависимости от времени;

в) момент времени t₀, когда угол между скоростью и ускорением равен

3.17.Компоненты скорости частицы изменяются со временем по законам , где и -константы. Найти модули скорости и ускорения, а также угол между векторами скорости и ускорения.

3.18.Зависимость координат движения частицы от времени имеет вид .

а) определить радиус-вектор частицы , скорость , ускорение , а также их модули.

б) вычислить скалярное произведение векторов и .

в) вычислить скалярное произведение векторов .

г) найти уравнение траектории, изобразить ее график и указать направление движения частицы по траектории.

3.19.Точка движется в плоскости ху по закону , где А и -положительные постоянные. Найти: а) путь, пройденный точкой за время ; б) угол между скоростью и ускорением точки.

3.20.По графику зависимости ускорения от времени (рис.6) построить графики зависимости , считая, что .

а(м/с²)

1

0 1 2 3 4 t ( c )

-1

Рис. 6

3.21.Лодку с крутого берега тянут за веревку, выбирая ее с постоянной по модулю скоростью V. Найдите зависимость модуля скорости лодки от угла между веревкой и горизонтальным направлением.