2.1. Ізотропна пластинка з криволінійним отвором

Розглянемо нескінченну ізотропну пластинку товщиною , яка послаблена криволінійним отвором у вигляді правильного  ‑ кутника із закругленими кутами. Сумістимо із серединною площиною пластинки, криволінійний отвір якої обмежений гладким контуром , комплексну площину . Систему прямокутних і полярних координат в цій площині оберемо так, щоб початок відліку співпадав з центром отвору, а полярна вісь – з віссю абсцис і віссю симетрії отвору (рис. 2.1).

Нехай раціональна функція

(2.1)

здійснює конформне відображення зовнішності одиничного кола ( ) в площині на область, яку займає серединна площина пластинки. Тут – характерний розмір отвору (не обмежуючи загальності, вважаємо ); ; – параметр, який визначає відхилення форми многокутника від кола. При , функція (2.1) реалізує конформне відображення на зовнішність зовнішності еліпса в площині ; при , – зовнішності трикутника із закругленими кутами.

Припустимо, що до контуру в серединній площині пластинки або його частини прикладено нормальні та дотичні зусилля (рис. 2.1), а напружений стан на нескінченності обмежений і зводиться до рівномірно розподілених зусиль і , що діють вздовж координатних осей.

Рис. 2.1. Схема навантаження пластинки

Для визначення компонент вектора зміщення точок контуру використаємо граничні умови першої і другої основних задач плоскої задачі теорії пружності

; (2.2)

, (2.3)

де введено позначення ;

; ; – модуль зсуву матеріалу пластинки; , – комплексні потенціали Мусхелішвілі; ; ; – кут між нормаллю до контуру і додатним напрямком осі ; – коефіцієнт Пуассона матеріалу пластинки; , – компоненти вектора зміщення точок контуру .

При заданому навантаженні на пластинку функції , мають таку структуру

;

. (2.4)

Тут , – голоморфні в області функції; - головний вектор зовнішніх зусиль, прикладених до контуру ; ; .

З урахуванням (2.4) граничну умову (2.2) подамо у вигляді

. (2.5)

Помножимо (2.5) на і проінтегруємо по контуру . Використовуючи властивості інтегралів типу Коші, подання (2.4) і співвідношення

, , (2.6)

знаходимо після певних перетворень

, (2.7)

де - точка на контурі , яка фіксує однозначну вітку логарифма в області .

У результаті додавання граничних умов (2.2), (2.3) одержимо співвідношення для визначення компонент вектора зміщення контурних точок через функцію і компоненти контурного навантаження

, . (2.8)

Встановимо граничне значення для функції при . Використовуючи формулу Сохоцького-Племеля

, (2.9)

із (2.7) визначимо

. (2.10)

Якщо головний вектор силового навантаження на контур отвору пластинки відмінний від нуля ( ), то функції , будуть багатозначними при однозначних зміщеннях. У такому випадку праву частину (2.10) зручніше виразити через однозначні функції , .

Коли проведемо в (2.10) інтегрування за частинами з використанням залежностей

; ;

, (2.11)

отримаємо

. (2.12)

Підставляючи (2.10) або (2.12) в умову (2.8), одержимо після певних перетворень і розділення дійсних та уявних частин

;

(2.13)

або

;

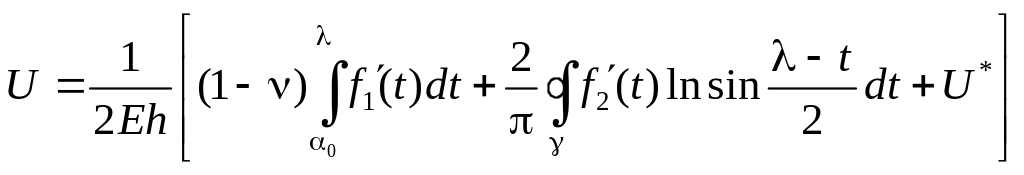, (2.14)

де

;

; (2.15)

, - довільні сталі; - модуль Юнга матеріалу пластинки.

При виведенні співвідношень (2.13), (2.14) враховано залежності

; .

Як видно із формул (2.13) – (2.15), компоненти вектора зміщення контурних точок пластинки визначаються з точністю до довільних сталих, які характеризують її жорстке зміщення.

Нормальна і дотична складові вектора зміщення з величинами , зв’язані формулою

. (2.16)

Для визначення компонент тензора деформації в контурних точках розглянемо відому залежність

, (2.17)

де , - відносне видовження контуру і кут повороту нормалі до нього;

; .

Цю залежність можна перетворити до вигляду:

. (2.18)

Коли підставимо в (2.18) замість його значення з (2.8), одержимо

. (2.19)

З урахуванням (2.12) після проведення диференціювання по із (2.19) знаходимо

;

. (2.20)

Тут введено позначення

;

; (2.21)

.

Якщо величини, відзначені зірочками, будуть відомі, то компоненти напружено-деформованого стану в точках контуру на підставі (2.18), (2.21) можна визначити за формулами

; ;

; , (2.22)

де ; ; .

Коли підставимо (2.20) в (2.22), знаходимо

;

, . (2.23)

Тут

; .

Кільцеві зусилля на контурі на підставі закону Гука знаходимо за формулою

. (2.24)

Якщо в (2.13)-(2.15), (2.20)-(2.24) підставити , то одержимо відповідні залежності для нескінченної пластинки з круговим отвором.