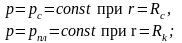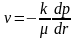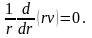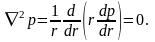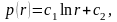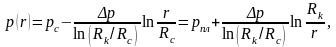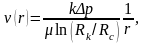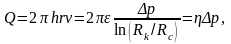- •§ 1. Кинематика сплошной среды
- •§ 2. Элементы теории деформаций
- •О скоростях деформаций
- •§ 3. Динамические величины и элементы теории напряжений
- •§ 4. Источник и сток в пространстве.
- •Тензоры
- •§ 1. Тензорная алгебра
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •Уравнением моментов
- •§ 3. Уравнения состояния (математические модели)
- •§ 4. Уравнения состояния гидромеханики
- •§ 1. Линейные стационарные задачи фильтрации.
- •Jules Dupuit Существенный вклад в развитие теории напорного и безнапорного движения грунтовых вод внес (Boussinesq) Жозеф Валантен Буссинеск (1842-1929 гг.) и Филипп Форхгеймер (1852-1933 гг.).
- •§ 2. Основные уравнения теории фильтрации
- •§ 3 Линейные уравнения и граничные задачи фильтрации.
- •1. Модель ламинарной фильтрации ньютоновских однородных жидкостей в изотропной среде
- •5. Нелинейный закон фильтрации
- •Решение линейных стационарных задач фильтрации (формула дюпюи и ее обобщения)
- •1. Первая основная граничная задача фильтрации
- •Вторая основная граничная задача фильтрации
- •3. Третьая основная граничная задача фильтрации
- •Основной показатель
- •4. Четвертая основная граничная задача фильтрации
- •5. Плоская фильтрация в вертикально-трещиноватом пласте
- •6. Определение расхода в неоднородном анизотропном пласте
- •7. Несовершенное вскрытие пластов
- •§ 5. Общие задачи механики деформируемого твердого тела в бурении и разработке нефтяных и газовых месторождений
- •§ 6. Мгновенные уравнения состояния и критерии прочности
- •§ 8. Общая система уравнений механики деформируемого твердого тела
- •Задачи гидромеханики в бурении
- •§ 1. Базовые задачи гидродинамики при промывке и цементировании скважин
- •§ 2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •§ 3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
5. Нелинейный закон фильтрации
Экспериментально установлено, что иногда линейный закон фильтрации жидкости (2.58) нарушается и зависимость между и принимает вид выпуклой или вогнутой кривой, как показано на рис. 11.
Рис. 11. Возможные виды нелинейного закона фильтрации
Основные причины проявления нелинейных эффектов следующие:
высокая скорость фильтрации, когда параметр Рейнольдса превышает критическое значение (зависимость изображена кривой 1 на рис. 11);
ламинарная фильтрация жидкостей с неньютоновскими свойствами (кривая 2);
малая скорость фильтрации в слабопроницаемых и неоднородных пластах (кривая 2).
Предложены различные аппроксимации нелинейных зависимостей. Например, кривая 1 чаще всего описывается двучленным законом фильтрации
, |
(2.62) |
а кривая 2 – законом фильтрации с предельным градиентом
|
(2.63) |
где, по данным Е. М. Минского, , а, по данным Б. И. Султанова, ; - эффективный диаметр пор; - предельное напряжение сдвига.
В общем случае к обоим типам кривых применимы степенная и кусочно-линейная аппроксимации
, |
(2.64) |
, |
(2.65) |
которыми удобно пользоваться при расчетах. Здесь - параметры модели; - характерное значение градиента давления; - безразмерная функция, описывающая ломаную линию (см. рис. 11).
Лекция 4
Решение линейных стационарных задач фильтрации (формула дюпюи и ее обобщения)
Одна из основных практически важных стационарных задач фильтрации – определение расхода жидкости при поглощении или проявлении пласта, искусственном нагнетании жидкости в пласт или отборе ее из пласта, а также определение параметров пласта и призабойной зоны при гидродинамических испытаниях скважин.
1. Первая основная граничная задача фильтрации
(пласт
однородный изотропный пористый
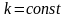 )
)
однородной
невесомой жидкостью вязкости
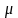 заполнены поры пласта
заполнены поры пласта
режим
ламинарный жесткий
или установившийся
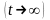
Простейшее решение этой задачи базируется на следующих предпосылках:
однородный изотропный пористый, трещиноватый или трещиновато-пористый пласт проницаемостью ограничен непроницаемыми плоскостями
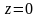 и
и
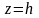 (кровля и подошва пласта) и проницаемыми
цилиндрическими поверхностями
(кровля и подошва пласта) и проницаемыми
цилиндрическими поверхностями
 (стенка скважины),
(стенка скважины),
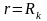 (поверхность питания), на которых
поддерживаются однородные граничные
условия
(поверхность питания), на которых
поддерживаются однородные граничные
условия
|
(3.55) |
поры пласта заполнены однородной невесомой жидкостью вязкости ;
фильтрация происходит при жестком или установившемся ламинарном режиме.
Основные уравнения теории фильтрации в этом случае запишутся в виде
|
(3.56) |
|
(3.57) |
Подстановка (3.56) в (3.57) дает простейший вид уравнения Лапласа
|
|
Общим решением этого уравнения является функция
|
(3.58) |
где
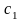 и
и
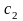 – постоянные интегрирования, определяемые
граничными условиями (3.55).
– постоянные интегрирования, определяемые
граничными условиями (3.55).
В результате получим решение первой основной граничной задачи фильтрации (3.55 – 3.57):
|
(3.59) |
|
(3.60) |
где
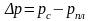 – заданный перепад давления между
скважиной и пластом.
– заданный перепад давления между
скважиной и пластом.
При
поглощении
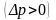 проявлении
проявлении
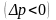 пласта объемный расход жидкости через
любую цилиндрическую поверхность
пласта объемный расход жидкости через
любую цилиндрическую поверхность
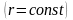 ,
в том числе и через стенку скважины,
,
в том числе и через стенку скважины,
|
(3.61) |
где
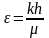 ;
;
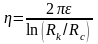 – соответственно коэффициент
гидропроводности, или просто
гидропроводность, и коэффициент
продуктивности, или просто продуктивность
пласта; размерность м3/Па.с.
– соответственно коэффициент
гидропроводности, или просто
гидропроводность, и коэффициент
продуктивности, или просто продуктивность
пласта; размерность м3/Па.с.
Формула (3.61) впервые получена французским инженером Дюпюи и поэтому названа его именем.