Тема 2. Функції.

1. Моделювання безперервних та розривних процесів.

2. Побудова графіків.

3. Табличний спосіб задання функції.

4. Чисельний експеримент і його застосування щодо дослідження функції.

1. Моделювання безперервних та розривних процесів.

2. Побудова графіків.

3. Табличний спосіб задання функції.

4. Чисельний експеримент і його застосування щодо дослідження функції.

Тема 3. Вектори та їх застосування. Векторний добуток.

1. Поняття вектора та його властивості.

2. Дії з векторами.

3. Векторний добуток.

1. Поняття вектора та його властивості.

Вектором називається прямолінійний відрізок (упорядкована пара точок). До векторів належить також і нульовий вектор, початок і кінець якого збігаються.

Довжиною (модулем) вектора називається відстань між початком і кінцем вектора.

(3.1)

Вектори називаються колінеарними, якщо вони розташовані на одній або паралельних прямих. Нульовий вектор колінеарний до будь-якого вектора.

Вектори називаються компланарними, якщо існує площина, який вони паралельні.

Колінеарні вектори завжди компланарні, але не всі компланарні вектори колінеарні.

Вектори називаються рівними, якщо вони колінеарні, однаково спрямовані й мають однакові модулі.

Усякі вектори можна привести до спільного початку, тобто побудувати вектори, відповідно рівні даним, що мають загальний початок. З визначення рівності векторів треба, що будь-який вектор має нескінченно багато векторів, рівних йому.

2. Д ії з векторами.

Під лінійними операціями над векторами розуміють операцію додавання векторів і операцію множення вектора на дійсне число.

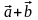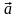С умою двох векторів і називається вектор, який напрямлений з початку вектора в кінець вектора , за умови, що початок вектора збігається з кінцем вектора (рис. 3.1).

Поряд із «правилом трикутника», яке сформульоване вище, часто користуються рівносильним йому «правилом паралелограма». Якщо вектори і зведені до спільного початку і на них побудований паралелограм, то сума є вектор, що збігається з діагоналлю цього паралелограма, яка виходить із спільного початку і (рис. 3.2).

Властивості операції додавання векторів

1. Комутативність .

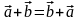2. Асоціативність .

3. Існування нейтрального елемента – нульового вектора – відносно додавання векторів, тобто для будь-якого вектора має місце рівність .

4 . Для кожного вектора існує протилежний вектор 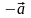, такий, що .

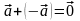Зауваження. Сума кількох векторів може бути знайдена за «правилом многокутника». Сумою кількох векторів є вектор, початок якого збігається з початком першого доданка, а кінець – з кінцем останнього за умови, що початок кожного наступного доданка збігається з кінцем попереднього (рис. 3.3).

Р ізницею двох векторів і , із яких перший називається зменшуваним, а другим від’ємником, називається вектор, який є сумою зменшуваного вектора і вектора, протилежного від’ємнику, тобто (рис. 3.4).

Добутком (або 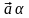) вектора на дійсне число називається вектор , колінеарний вектору , який має модуль, рівний добутку модуля вектора на модуль числа , тобто , та напрям, який збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо .