2. Диференціальні рівняння з подільними змінними, їх застосування в економіці.

Якщо у рівнянні

функція може бути подана у вигляді добутку двох співмножників, один з яких не містить змінної y, а другий – змінної х, тобто то рівняння набуде такого вигляду:

(8.7)

Рівняння (3.7) є рівнянням з відокремлюваними змінними. Оскільки похідна то маємо:

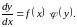
Обидві частини останнього рівняння помножимо на і поділимо на У результаті дістанемо рівняння з відокремленими змінними:

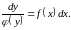(8.8)

Інтегруючи рівність (3.8), маємо:

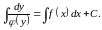(8.9)

Співвідношення (8.9) є загальним інтегралом рівняння (8.7).

Приклад 3. Проінтегрувати рівняння

► Перетворимо ліву частину рівняння

Відокремимо змінні, поділивши на

Інтегруючи, отримаємо загальний інтеграл рівняння:



Зауваження. Безпосередньою перевіркою можна переконатися, що і є розв’язками даного диференціального рівняння.

Приклад 4. Знайти частинний інтеграл рівняння

що задовольняє початкову умову

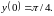
► Поділимо обидві частини рівняння на добуток дістанемо рівняння з відокремленими змінними Проінтегрувавши останнє рівняння, знаходимо

Підставимо в отриманий загальний інтеграл початкові дані 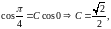отже, – частинний інтеграл. 

3. Лінійні диференціальні рівняння першого порядку. Однорідні диференціальні рівняння.

Функція називається однорідною функцією нульового виміру, якщо при множенні змінних і на довільний параметр значення функції не змінюється, тобто

Однорідна функція нульового виміру може бути подана у вигляді Дійсно, нехай є однорідною функцією нульового виміру. Це означає, що змінні і можна помножити на довільний параметр 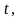і значення заданої функції в цьому випадку не зміниться. Нехай 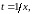тоді

Диференціальне рівняння називається однорідним, якщо функція є однорідною функцією нульового виміру. Таким чином, однорідне диференціальне рівняння можна подати у вигляді

(8.10)

Однорідне рівняння (8.10) можна звести до рівняння з відокремлюваними змінними, підстановкою де – нова функція. Диференціюючи рівність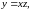 отримаємо:

Підставивши вирази для і 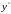у рівняння (8.10), отримаємо:

або

(8.11)

Рівняння (3.11) є рівнянням з відокремленими змінними і

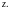
Інтегруючи, знаходимо

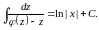(8.12)

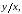Якщо в цьому виразі замінити його значенням то дістанемо інтеграл рівняння (8.10).

Приклад 3.5. Проінтегрувати рівняння

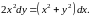
► Ділимо обидві частини рівності на 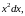отримаємо рівняння, правою частиною якого є функція відношення

Покладемо в ньому і 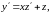отримаємо рівняння з відокремлюваними змінними

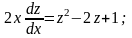
Інтегруючи та підставляючи замість z, отримаємо загальний інтеграл даного рівняння

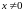При відокремленні змінних ми ділили на х і що можливо при і Безпосередньою перевіркою легко переконатися, що і є також розв’язками даного рівняння, але вони не входять у загальний інтеграл. 

^ Зі шкільного курсу таке рівняння відоме як рівняння, що виражає пряму пропорційність.

*^* Асимптотою кривої можна вважати пряму, до якої необмежено наближається довільна точка цієї кривої, віддаляючись в нескінченість. Строге означення асимптоти розглядається в теорії границь з математичного аналізу.

13