2.3. Інтегрування частинами

Якщо на множині 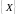функції і 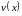неперервні разом із похідними, то має місце формула інтегрування частинами:

(7.5)

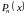
Розглянемо три групи інтегралів, для обчислення яких застосовується формула (1.5). Нехай  многочлен степеня n, а множником під інтегралом є одна з функцій, поданих у фігурних дужках. Рекомендований вибір u і dv наведений у дужках після знака рівності.

1. Інтеграли виду

Однократне застосування формули (7.5) дозволяє знизити на одиницю степінь многочлена під інтегралом, n-кратне застосування формули (7.5) зводить дані інтеграли до табличних.

Приклад 11

►



2. Інтеграли виду

Приклад 12

►



Приклад 13

►



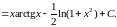
3. Інтеграли виду

Це так звані “циклічні” інтеграли. Після двократного інтегрування частинами у правій частині рівності одержимо початковий інтеграл I з деяким коефіцієнтом. Із отриманого лінійного рівняння треба знайти I.

Приклад 14

►

У правій частині одержали початковий інтеграл. Перепишемо останню рівність у вигляді:

З цього рівняння знайдемо I



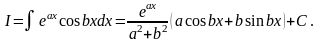
Зауваження. Зазначені три групи інтегралів не охоплюють усіх інтегралів, що беруться за допомогою інтегрування частинами.

2.4. Інтегрування деяких функцій, що містять квадратний тричлен

Розглянемо інтеграли виду

(7.6)

Схема обчислення інтегралів (7.6):

1) винести за знак інтеграла коефіцієнт a при x²;

2) виділити повний квадрат у квадратному тричлені (для цього зручно ввести нову змінну, що дорівнює половині похідної квадратного тричлена);

3) розбити інтеграл, що утворився, на два інтеграли, поділивши вираз у чисельнику на знаменник.

Приклад 15

►

<

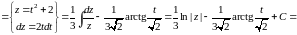
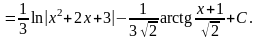Приклад 1.16

►

<

Тема 8. Диференціальні рівняння

1. Диференціальні рівняння та їх класифікація. Типи розв’язків диференціальних рівнянь.

2. Диференціальні рівняння з подільними змінними, їх застосування в економіці.

3. Лінійні диференціальні рівняння першого порядку. Однорідні диференціальні рівняння.

1. Диференціальні рівняння та їх класифікація. Типи розв’язків диференціальних рівнянь.

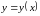Звичайним диференціальним рівнянням називається рівняння, що зв’язує незалежну змінну шукану функцію і її похідні до деякого порядку включно.

Загальний вигляд диференціального рівняння:

Порядком диференціального рівняння називається порядок найвищої похідної від шуканої функції, що входить у рівняння.

Загальний вигляд диференціального рівняння другого порядку:

Звичайне диференціальне рівняння першого порядку має вигляд:

Іноді рівняння першого порядку записується у вигляді

У цьому випадку за невідому функцію можна взяти як х, так і у.

Розв’язком диференціального рівняння називається будь-яка функція яка при підстановці в рівняння перетворює його на тотожність.

Розв’язок, заданий неявно, тобто у вигляді називається інтегралом диференціального рівняння.

Приклад 1. Довести, що функція є розв’язком рівняння

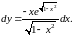► Покладемо знайдемо Підставивши значення у і в дане рівняння, отримаємо тотожність:



Приклад 2. Показати, що рівняння яке визначає у як неявну функцію від х, є інтегралом диференціального рівняння

► Диференціюючи дане рівняння, знайдемо

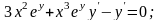
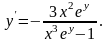
Підставивши в рівняння, одержимо тотожність:

