
- •Тема 1. Наближені обчислення.
- •Наближені обчислення. Типи похибок.
- •Абсолютна та відносна похибки.
- •Дії з наближеними числами.
- •Обчислення значень виразів за допомогою обчислювальних засобів. Обробка результатів вимірювання.
- •Тема 2. Функції.
- •Тема 3. Вектори та їх застосування. Векторний добуток.
- •Д ії з векторами.
- •Властивості операції додавання векторів
- •Властивості операції множення вектора на число
- •Векторний добуток.
- •Алгебраїчні властивості векторного добутку
- •Геометричні властивості векторного добутку
- •Вираз векторного добутку через координати
- •Тема 4. Прямокутні координати та їх застосування.
- •Прямокутні координати та їх застосування.
- •Поділ відрізка у даному відношенні. Центр мас.
- •Полярна та циліндрична системи координат
- •Тема 5. Лінії на площині
- •Пряма лінія на площині.
- •1.1. Різні види рівнянь прямої на площині
- •1.2. Загальне рівняння прямої та його дослідження Нормальне рівняння прямої
- •1.3. Взаємне розташування прямих на площині
- •9.2.4. Відстань від точки до прямої на площині. Рівняння бісектрис кута між прямими
- •Лінії другого порядку.
- •2.1.1. Канонічне рівняння еліпса
- •2.1.2. Дослідження форми еліпса
- •2.1.3. Інші види та побудова еліпса
- •2.2.1. Канонічне рівняння гіперболи
- •2.2.2. Дослідження форми гіперболи
- •2.2.3. Асимптоти гіперболи. Інші види гіперболи
- •2.2.5. Ексцентриситет і директриси еліпса та гіперболи
- •Парабола
- •2.3.1. Канонічне рівняння параболи
- •2.3.2. Дослідження форми та побудова параболи
- •Тема 6. Похідна
- •Геометричний та фізичний зміст похідної.
- •Властивості похідной
- •Д иференціал функції, його геометричний зміст та застосування до наближених обчислень.
- •Тема 7. Інтеграл
- •Інтеграл
- •Основні властивості невизначеного інтеграла
- •Методи обчислення інтегралів
- •2.1. Безпосереднє інтегрування
- •2.2. Метод заміни змінної (метод підстановки)
- •2.3. Інтегрування частинами
- •2.4. Інтегрування деяких функцій, що містять квадратний тричлен
- •Тема 8. Диференціальні рівняння
- •Диференціальні рівняння та їх класифікація. Типи розв’язків диференціальних рівнянь.
- •Диференціальні рівняння з подільними змінними, їх застосування в економіці.
- •Лінійні диференціальні рівняння першого порядку. Однорідні диференціальні рівняння.
Лінії другого порядку.
Еліпс.
Еліпсом називається множина всіх точок площини, сума відстаней від кожної з яких до двох даних точок тієї ж площини, які називаються фокусами еліпса, є величина стала, причому більша, ніж відстань між фокусами.
2.1.1. Канонічне рівняння еліпса
Щоб
вивести рівняння еліпса, візьмемо на
площині дві точки
 і
і
 – фокуси еліпса і розмістимо ДПСК так,
щоб вісь абсцис проходила через фокуси,
а початок координат ділив відрізок
– фокуси еліпса і розмістимо ДПСК так,
щоб вісь абсцис проходила через фокуси,
а початок координат ділив відрізок
 навпіл (рис.10.4).
навпіл (рис.10.4).
П означимо
відстань між фокусами, яку називають
фокальною,
через 2с,
тобто
означимо
відстань між фокусами, яку називають
фокальною,
через 2с,
тобто
 ,
тоді фокуси матимуть у вибраній ДПСК
координати
,
тоді фокуси матимуть у вибраній ДПСК
координати
 та
та
 .
Нехай
– довільна точка еліпса. Відстані
.
Нехай
– довільна точка еліпса. Відстані
 та
та
 називаються фокальними
радіусами
точки М.
Покладемо
називаються фокальними
радіусами
точки М.
Покладемо
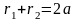 (*),
тоді згідно означення еліпса 2а
– величина стала, причому
(*),
тоді згідно означення еліпса 2а
– величина стала, причому
 ,
тобто
,
тобто
 .
Тоді за формулою (8.15) знаходимо
.
Тоді за формулою (8.15) знаходимо
 і
і
 .
Підставивши знайдені значення
.
Підставивши знайдені значення
 і
і
 в рівність (*), отримаємо рівняння
еліпса
в рівність (*), отримаємо рівняння
еліпса
 .
(5.6)
.
(5.6)
Перенесемо
один з доданків з лівої частини рівняння
в праву
 ,
піднесемо до квадрату:
,
піднесемо до квадрату:
 ,
отримаємо
,
отримаємо
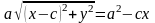 ,
знову піднесемо до квадрату
,
знову піднесемо до квадрату
 ,
тобто
,
тобто
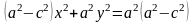 .
Так як
,
то
.
Так як
,
то
 ,
тому покладемо
,
тому покладемо
 ,
(5.7)
,
(5.7)
тоді
останнє рівняння набуде вигляду
 або
або
 .
(5.8)
.
(5.8)
Так як координати х і у будь-якої точки М еліпса задовольняє рівняння (10.6), то вони задовольняють і рівняння (10.8).
Справедливим
є і обернене твердження: якщо координати
точки М(х;
у)
задовольняють рівняння (10.8), то вона
належить еліпсу. Нехай М(х;
у)
– довільна точка, координати якої
задовольняють рівняння (10.8). З рівняння
(10.8) маємо
 (**),
тоді
(**),
тоді
 ,
звідки
,
звідки
 .
Підставивши рівність (**) в формули
фокальних радіусів, отримаємо
.
Підставивши рівність (**) в формули
фокальних радіусів, отримаємо
 і
і
 .
.
Але
так як
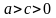 і
,
то
і
,
то
 і
і
 .
Звідки
.
Звідки
 і
і
 ,
значить,
,
тобто точка М(х;
у)
дійсно належить еліпсу.
,
значить,
,
тобто точка М(х;
у)
дійсно належить еліпсу.
Рівняння (10.8) називається канонічним рівнянням еліпса.
Приклад.
10.7.
Скласти канонічне рівняння еліпса, який
проходить через точки
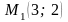 і
і
 ,
якщо його фокуси лежать на осі абсцис
симетрично відносно початку координат.
,
якщо його фокуси лежать на осі абсцис
симетрично відносно початку координат.
За
умовою дані точки належать еліпсу,
значить, їхні координати задовольняють
рівняння (10.8), тобто
 і
і
 .
Розв’язуючи цю систему рівнянь, знаходимо
.
Розв’язуючи цю систему рівнянь, знаходимо
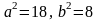 .
Отже, шукане рівняння має вигляд
.
Отже, шукане рівняння має вигляд
 .
.
2.1.2. Дослідження форми еліпса
Д ля
дослідження форми еліпса складемо
порівняльну таблицю, в лівому стовпці
якої будемо аналізувати властивості
його рівняння, а в правому – записувати
відповідні властивості фігури на площині
відносно обраної ДПСК.
ля
дослідження форми еліпса складемо
порівняльну таблицю, в лівому стовпці
якої будемо аналізувати властивості
його рівняння, а в правому – записувати
відповідні властивості фігури на площині
відносно обраної ДПСК.
Т аблиця 5.1
Властивості канонічного рівняння еліпса |
Властивості фігури |
1. Координати точки О(0; 0) на задовольняють рівняння. |
1. Еліпс не проходить через початок координат. |
2. Система, складена з рівняння еліпса (ІІ-го порядку) та прямої (І-го порядку), має не більше двох розв’язків: |
2. Пряма перетинає еліпс не більш як в двох точках: |
1)
|
1)
еліпс з віссю абсцис має дві спільні
точки з координатами
|
2) . |
2)
еліпс з віссю ординат має дві спільні
точки з координатами
|
3.
Області зміни х
і у
визначаються нерівностями
і
|
3.
Всі точки еліпса знаходяться всередині
прямокутника, обмеженого прямими
|
4. Змінні х та у входять до рівняння в парних ступенях. |
4. Еліпс симетричний відносно координатних осей, і, значить, відносно початку координат. |
5.
З
рівняння маємо
|
5.
При зростанні
|
Прямокутник,
зображений на рис. 10.5, тобто обмежений
прямими
 та
та
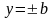 ,
називається основним
прямокутником еліпса.
,
називається основним
прямокутником еліпса.
Врахувавши всі властивості фігури, вказані в таблиці 10.1, можна зробити висновок, що еліпс має форму, зображену на рис. 10.6.
Точки
 називаються вершинами
еліпса.
Відрізок
називаються вершинами
еліпса.
Відрізок
 ,
де
,
де
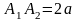 ,
,
 ,
,
 ,
називається великою
віссю еліпса,
а
,
називається великою
віссю еліпса,
а
 ,
,
 – великою
напіввіссю еліпса;
відповідно відрізок
– великою
напіввіссю еліпса;
відповідно відрізок
 ,
де
,
де
 ,
називається малою
віссю еліпса,
а
,
називається малою
віссю еліпса,
а
 – малою
напіввіссю еліпса.
Вісі
і
– малою
напіввіссю еліпса.
Вісі
і
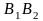 є осями
симетрії еліпса,
а точка О
– центром
симетрії
(або просто центром)
еліпса.
є осями
симетрії еліпса,
а точка О
– центром
симетрії
(або просто центром)
еліпса.
Приклади. 10.8. Скласти канонічне рівняння еліпса, якщо фокусна відстань дорівнює 10, а мала вісь дорівнює 6.
Так
як мала вісь дорівнює 6, то мала напіввісь
–3, тобто
 ,
,
 .
За формулою (10.7)
.
За формулою (10.7)
 ,
тоді
,
тоді
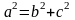 ,
значить,
,
значить,
 .
Отже,
.
Отже,
 .
.
10.9.
Визначити довжини осей та координати
фокусів еліпса
 .
.
Розділивши
обидві частини рівняння на 1176, зведемо
його до канонічного вигляду
 .
Звідси
.
Звідси
 ,
,
 .
За формулою (10.7) маємо
,
звідки
.
За формулою (10.7) маємо
,
звідки
 ,
отже,
,
отже,
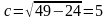 ,
значить
,
значить
 і
і
 .
.


 і
і
 ;
; і
і
 .
. ,
тобто
,
тобто
 та
та

 ,
,
 ,
,
 ,
,
(рис. 10.5).
,
,
(рис. 10.5).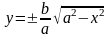 і
і
 .
.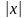 від 0 до а
величина
від 0 до а
величина
 спадає від b
до 0, а при зростанні
від b
до 0 величина
спадає від 0 до а.
спадає від b
до 0, а при зростанні
від b
до 0 величина
спадає від 0 до а.