9.2.4. Відстань від точки до прямої на площині. Рівняння бісектрис кута між прямими

Н ехай задано пряму загальним рівнянням і точку . Відстань d (рис. 9.24) точки M₀ від прямої l дорівнює модулю проекції вектора , де – довільна точка прямої l, на напрям нормального вектора прямої l . Отже, . Оскільки, , то , значить 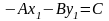, тому відстань від точки до прямої знаходиться за такою формулою:

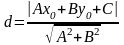. (9.30)

Зауваження. Число d завжди додатне, бо це відстань, а ось величина  може бути і додатною і від’ємною. Відхиленням  точки від прямої із загальним рівнянням називається число , яке додатним, тобто  = d, якщо точки і лежать по різні сторони від прямої , і від’ємним, тобто  = –d, якщо ці точки лежать по один бік від даної прямої. З формули (9.30) випливає, що відхилення обраховується так:

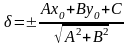, (9.31)

де знак знаменника повинен мати знак, протилежний до знака коефіцієнта С.

Приклад 19. Визначити відстань між паралельними прямими і .

 Розв’язання задачі зводиться до визначення відстані від довільної точки однієї прямої до іншої. Візьмемо точку на прямій , для цього покладемо в рівнянні цієї прямої і знайдемо відповідну ординату точки , отже, точка має координати . Визначимо тепер за формулою (9.31) відстань від точки до прямої :

.

Приклад 20. Знайти площу квадрата, дві сторони якого лежать на паралельних прямих . і .

 Аналогічно попередньому прикладу 9.33 візьмемо точку і знайдемо за формулою (9.31) відстань від цієї точки до прямої , а відстань між цими прямими для квадрата є довжиною його сторони, значить, .

Бісектриси кутів, утворених прямими, є, як відомо, геометричними місцями точок, рівновіддалених від цих прямих. Якщо прямі задані загальними рівняннями : А₁х+В₁у+С₁=0, : А₂х+В₂у+С₂=0, причому , тобто прямі не є паралельними, то для будь-якої точки 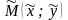, що лежить на одній з бісектрис, маємо, використовуючи формулу (9.31),

.

Оскільки точка – довільна точка бісектриси, то її можна позначити . Враховуючи, що вирази, які стоять під знаком модуля, можуть мати різні знаки, отримаємо для однієї бісектриси рівняння , а для іншої рівняння – 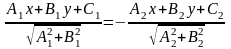. Таким чином, рівняння обох бісектрис можна записати у вигляді:

. (9.32)

Приклад 21. Дано вершини трикутника: , 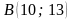, . Скласти рівняння бісектриси кута А.

 І спосіб. Знайдемо, користуючись формулою (9.13), рівняння тих сторін трикутника, які утворюють кут А: і . Тепер за формулою (9.32) складемо рівняння бісектрис між цими прямими: . Так як нам потрібен гострий кут, то обираємо варіант із знаком мінус, тобто . Після спрощення виразу та зведення подібних доданків одержимо рівняння .

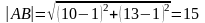ІІ спосіб. Використаємо тут властивість бісектриси. Нехай D – точка перетину бісектриси зі стороною BC. За властивістю бісектриси внутрішнього кута випливає, що . Але i . Значить, . Знайдемо тепер за формулами (8.22) координати точки D: і , тобто . Складемо за формулою (9.13) рівняння прямої, що проходить через точки А і D:

. 
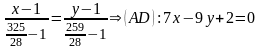