
- •Раздел 1. Линейные цепи постоянного тока
- •1.1. Краткие теоретические сведения
- •1.2.Лабораторная работа №1. Исследование резистивной цепи
- •1.3. Лабораторная работа №2. Исследование линии передачи
- •Раздел 2. Пассивные двухполюсники
- •Раздел 3. Трехфазные цепи
- •Раздел 4. Индуктивно − связанные цепи
- •Раздел 5. Линейные цепи периодического
- •5.1. Краткие теоретические сведения
- •5.2. Лабораторная работа №9. Линейные цепи периодического
- •Раздел 6. Переходные процессы в линейных
- •6.1. Краткие теоретические сведения
- •6.2. Лабораторная работа №10. Переходные процессы в линейных
- •Раздел 7. Электрические цепи
- •7.1. Краткие теоретические сведения
- •7.2. Лабораторная работа №11. Исследование цепей
- •В.1. Правила внутреннего распорядка и техники безопасности при выполнении лабораторных работ
- •В.2. Общие методические рекомендации и указания по выполнению лабораторных работ
- •В.3. Условные графические обозначения элементов электрических схем
- •Раздел 1. Линейные цепи постоянного тока
- •1.1. Краткие теоретические сведения
- •1.1.1. Основные понятия и определения
- •1.1.2. Законы Кирхгофа
- •1.1.3. Потенциальная диаграмма
- •1.1.4. Метод наложения
- •1.1.5. Линия передачи
- •1.2. Лабораторная работа №1
- •1.2.1. Цель и краткое содержание работы
- •1.2.3. Порядок выполнения измерений
- •1.2.4. Расчетная часть
- •1.2.5. Содержание отчета
- •1.2.6. Контрольные вопросы
- •1.3. Лабораторная работа №2
- •1.3.1. Цель и краткое содержание работы
- •1.1.1. Основные понятия и определения;
- •1.1.5. Линия передачи.
- •1.3.2. Описание лабораторного стенда
- •1. Напряжение на входе схемы устанавливать не более 20 в.
- •2. Избегать работы схемы при токах нагрузки более 0,3 а на протяжении более 10 мин.
- •1.3.3. Порядок выполнения измерений
- •1.3.4. Расчетная часть
- •1.3.5. Содержание отчета
- •1.3.6. Контрольные вопросы
- •Раздел 2. Пассивные двухполюсники
- •2.1. Краткие теоретические сведения
- •2.1.1. Основные понятия и определения
- •2.1.2. Основы символического метода
- •2.1.3. Комплексное представление элементов электрической цепи
- •2.1.4. Расчет цепей гармонического тока
- •2.1.5. Мощность в цепи гармонического тока
- •2.1.6. Резонанс в цепи гармонического тока
- •2.2. Лабораторная работа №3
- •2.2.1. Цель и краткое содержание работы
- •2.2.3. Порядок выполнения измерений
- •2.2.4. Расчетная часть
- •2.2.5. Содержание отчета
- •2.2.6. Контрольные вопросы
- •2.3. Лабораторная работа №4
- •2.3.1. Цель и краткое содержание работы
- •2.3.4. Расчетная часть
- •2.3.5. Содержание отчета
- •2.3.6. Контрольные вопросы
- •2.4. Лабораторная работа №5
- •2.4.1. Цель и краткое содержание работы
- •2.1.4. Расчет цепей гармонического тока;
- •2.1.5. Мощность в цепи гармонического тока;
- •2.1.6. Резонанс в цепи гармонического тока.
- •2.4.2. Описание лабораторного стенда
- •2.4.3. Порядок выполнения измерений
- •2.4.4. Расчетная часть
- •2.4.5. Содержание отчета
- •2.4.6. Контрольные вопросы
- •Раздел 3. Трехфазные цепи
- •3.1. Краткие теоретические сведения
- •3.1.1. Основные понятия и определения
- •3.1.2. Схемы соединения трехфазных цепей
- •3.1.3. Расчет трехфазных цепей
- •3.1.4. Мощность в трехфазной цепи
- •3.2. Лабораторная работа №6
- •3.2.1. Цель и краткое содержание работы
- •3.2.3. Порядок выполнения измерений
- •3.2.4. Расчетная часть
- •3.2.5. Содержание отчета
- •3.2.6. Контрольные вопросы
- •3.3. Лабораторная работа №7
- •3.3.1. Цель и краткое содержание работы
- •3.3.3. Порядок выполнения измерений
- •3.3.4. Расчетная часть
- •3.3.5. Содержание отчета
- •3.3.6. Контрольные вопросы
- •Раздел 4. Индуктивно − связанные цепи
- •4.1. Краткие теоретические сведения
- •4.1.1. Основные понятия и определения
- •4.1.2. Расчет электрических цепей
- •4.1.3. Определение одноименных зажимов
- •4.1.4. Экспериментальное определение
- •4.2. Лабораторная работа №8
- •4.2.1. Цель и краткое содержание работы
- •4.2.3. Порядок выполнения измерений
- •4.2.4. Расчетная часть
- •4.2.5. Содержание отчета
- •4.2.6. Контрольные вопросы
- •Раздел 5. Линейные цепи периодического
- •5.1. Краткие теоретические сведения
- •5.1.1. Основные понятия и определения
- •5.1.2. Расчет цепей негармонического тока
- •5.2. Лабораторная работа №9
- •5.2.1. Цель и краткое содержание работы
- •5.1.1. Основные понятия и определения;
- •5.1.2. Расчет цепей негармонического тока.
- •5.2.2. Описание лабораторного стенда
- •5.2.3. Работа с портативным осциллографом hps-1401
- •5.2.4. Порядок выполнения измерений
- •5.2.5. Расчетная часть
- •5.2.6. Содержание отчета
- •5.2.7. Контрольные вопросы
- •Раздел 6. Переходные процессы в линейных
- •6.1. Краткие теоретические сведения
- •6.1.1. Понятие переходного процесса.
- •6.1.2. Сведения из теории линейных
- •6.1.3. Расчет начальных условий
- •6.1.4. Расчет переходного процесса
- •6.1.5. Расчет переходного процесса
- •6.1.6. Порядок расчета переходных процессов
- •6.2. Лабораторная работа №10
- •6.2.1. Цель и краткое содержание работы
- •6.2.3. Работа с портативным осциллографом hps-1401
- •6.2.4. Порядок выполнения измерений
- •6.2.5. Расчетная часть
- •6.2.6. Содержание отчета
- •6.2.7. Контрольные вопросы
- •Раздел 7. Электрические цепи
- •7.1. Краткие теоретические сведения
- •7.1.1. Основные понятия и определения
- •7.1.2. Полупроводниковый диод
- •7.1.3. Полупроводниковый стабилитрон
- •7.1.4. Динистор
- •7.2. Лабораторная работа №11
- •7.2.1. Цель и краткое содержание работы
- •7.2.3. Порядок выполнения измерений
- •7.2.4. Расчетная часть
- •7.2.5. Содержание отчета
- •7.2.6. Контрольные вопросы
1.1.4. Метод наложения
К свойствам линейных электрических цепей относится принцип независимости действия ЭДС, который лежит в основе метода расчета, получившего название метода наложения. Согласно ему в линейной электрической цепи действие, оказываемое каждой из ЭДС в отдельности, можно рассматривать независимо от действия других ЭДС. Другими словами, ток в k−й ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности.
При расчете цепей по методу наложения поступают следующим образом: поочередно рассчитывают частичные токи, возникающие от действия каждого из источников, мысленно удаляя из схемы остальные, но оставляя их внутренние сопротивления; затем находят токи в ветвях путем алгебраического сложения (с учетом направления) частичных токов.
Исключение источников означает следующее: источник ЭДС закорачивается, а ветвь с источником тока размыкается.
Заметим, что принципом наложения нельзя пользоваться для расчета баланса мощности, поскольку мощность - квадратичная функция тока.
1.1.5. Линия передачи
Баланс мощности характеризует распределение электрической энергии между источниками и приемниками. Немаловажное значение имеет также и то, каким закономерностям подчиняется процесс передачи энергии в различных системах, будь то линия электропередачи или линия передачи информации, поскольку для каждой из них характерен свой наиболее эффективный режим работы.
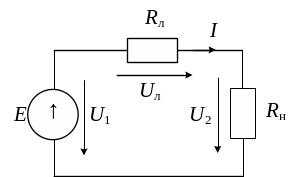
Независимо от назначения, каждая линия передачи представляет собой совокупность трех основных элементов: источника, собственно линии передачи и приемника (потребителя). Рассмотрим модель линии передачи, представленную на рис.1.5, где под сопротивлением Rл понимается сопротивление линии (суммарное сопротивление обоих проводов), а под Rн - сопротивление нагрузки (приемника).
|
Рис.1.5. Схема линии передачи
Под источником понимают генератор с ЭДС E, обладающий внутренним сопротивлением RE. При рассмотрении процессов в линии передачи для наглядности и без потери общности выводов целесообразно внутреннее сопротивление источника объединить с сопротивлением линии, сохранив его обозначение RЛ. Тогда расчетная модель линии передачи будет иметь вид, как на рис.1.6.
|
|
Рис.1.6. Модель линии передачи: E - ЭДС источника энергии; RН – сопротивление нагрузки (приемника); RЛ - сопротивление линии передачи и внутреннего сопротивления источника
|
По второму закону Кирхгофа (ЗНК) для рассматриваемой цепи можно записать
|
|
где U2 = IRН; UЛ = IRЛ.
Отсюда получим выражения для тока I и напряжения U2 на нагрузке
Заметим, что напряжение UE на зажимах реального источника ЭДС (рис.1.1,а) с внутренним сопротивлением RE также определяется по формуле (1.14):
|
|
На основании закона Джоуля-Ленца мощность, отдаваемая источником во внешнюю цепь, равна P1 =EI, а мощность, выделяющаяся в активных сопротивлениях, P = R I2. Для цепи рис.1.6 R=Rл + Rн.
В линиях передачи переменной величиной является сопротивление нагрузки Rн. Диапазон возможного изменения данного сопротивления определяет режимы работы линии передачи. Рассмотрим два предельных режима: режим холостого хода и режим короткого замыкания.
Режим холостого хода (х.х.). Данному режиму соответствует величина сопротивления нагрузки Rн = ∞. Тока в цепи нет (Iхх = 0), напряжение на линии UЛ.хх = 0, а напряжение U2хх, подводимое к нагрузке, равно ЭДС источника U2хх = E. Соответственно и мощности, выделяющиеся в линии и нагрузке, равны нулю.
Режим короткого замыкания (к.з.). В данном режиме сопротивление нагрузки RН = 0, мощность, выделяющаяся в нагрузке, также равна нулю, а ток в цепи достигает максимально возможного в данной линии значения - тока короткого замыкания
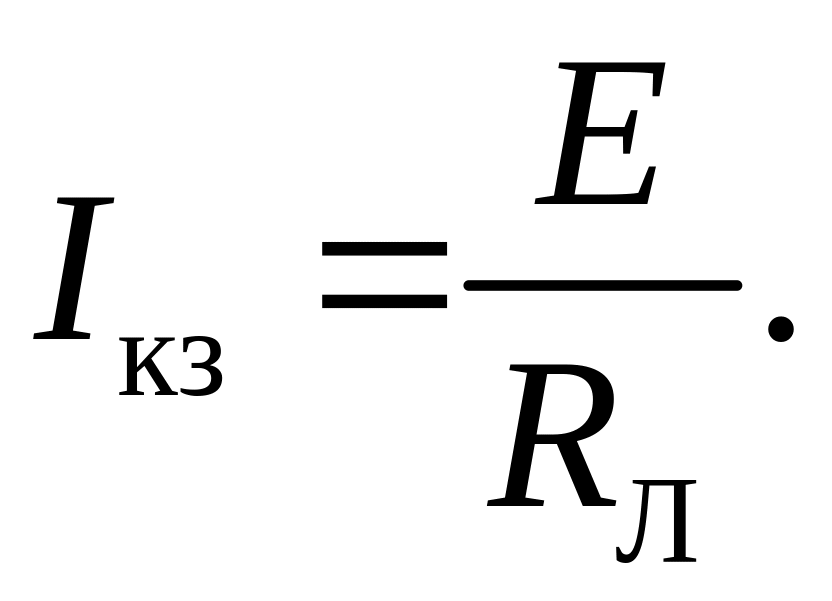
Очевидно, что напряжение на нагрузке при этом U2кз = 0, а напряжение UЛ на сопротивлении линии RЛ уравновешивает напряжение источника
UЛ = U1 = E.
Мощность P1кз, отдаваемая источником в режиме к.з., равна
P1кз = EIкз.
В соответствии с законом сохранения энергии эта мощность равна мощности PЛ, выделяющейся в сопротивлении линии RН ,
P1кз = PЛ = RЛ Iкз2 .
Режим короткого замыкания для большинства линий передач является аварийным.
При изменении сопротивления нагрузки RН в диапазоне (0,∞) ток в линии передачи принимает значения от Iкз до 0. В соответствии с (1.14) напряжение на нагрузке U2 в функции тока I изменяется по линейному закону от значения U2 = E в режиме холостого хода до U2 = 0 при коротком замыкании.
Мощность P1 = EI, отдаваемая источником, линейно зависит от тока, а мощность, выделяющаяся в линии, PЛ = RНI 2 изменяется по квадратичному закону. Мощность PЛ представляет собой потери, поэтому всегда стремятся к снижению ее величины.
Полезной является мощность, выделяющаяся в нагрузке. Она равна
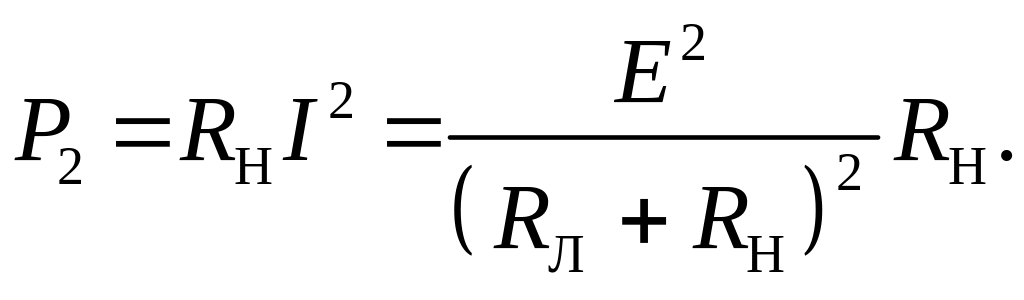
Как в режиме холостого хода, так и в режиме короткого замыкания P2=0. Из этого следует очевидный вывод о том, что функция P2(I) имеет по крайней мере один максимум в диапазоне изменения тока (0, Iкз). Для его определения следует взять производную от P2 по току и приравнять ее нулю. А поскольку ток I является функцией сопротивления нагрузки, то производную следует взять по RН:
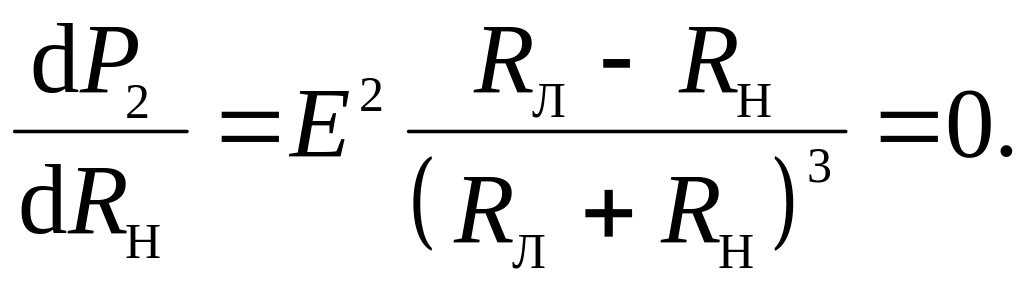
Таким образом, максимум мощности в нагрузке имеет место при выполнении условия
RЛ = RН .
Режим передачи максимальной мощности носит название согласованного режима и определяет возможности данной линии по передаче энергии потребителю. Соответствующая нагрузка RН носит название согласованной нагрузки. Ток, соответствующий данному режиму, равен половине тока короткого замыкания

Очевидно, что в согласованном режиме мощность, отдаваемая источником, поровну делится между линией и нагрузкой.
Параметром, характеризующим эффективность передачи энергии, служит коэффициент полезного действия (КПД) η, равный отношению мощности P2, потребляемой нагрузкой, к мощности P1 источника. Для рассматриваемой линии передачи
|
|
Отсюда следует, что КПД изменяется по линейному закону в функции тока I от η = 1 в режиме холостого хода до η = 0 в режиме короткого замыкания. В согласованном режиме η = 0,5.
На рис.1.7,а приведены графики изменения напряжений, мощностей и КПД в функции тока I, которые можно построить для конкретных параметров линии передачи по приведенным выше формулам.
|
|
Рис.1.7. Графики изменения напряжения на нагрузке, мощностей, КПД линии передачи (а) и график зависимости КПД от тока в реальной системе (б) |
|
Как видно из графика рис.1.7,а, мощность P2 , выделяющаяся в нагрузке, имеет максимум при токе, равном половине тока короткого замыкания Iкз (согласованный режим). При любой величине тока In сумма напряжения на нагрузке U2n и падения напряжения в линии UЛn равна ЭДС E.
В электроэнергетике, где осуществляется передача значительных мощностей, наиболее целесообразным является режим, при котором реализуется наибольший КПД. Поэтому энергетические системы работают в области малых (по сравнению с током короткого замыкания) токов.
Заметим, что в реальных линиях передачи КПД никогда не равен 1. Это связано с наличием потерь в реальном источнике (генераторе), что требует дополнительных затрат энергии, в том числе и в режиме холостого хода. Физически это обусловлено необходимостью совершения работы против кулоновских сил по разделению зарядов в источнике и поддержанию соответствующей разности потенциалов на его зажимах. Например, в синхронном генераторе, представляющем собой электрическую машину, напряжение на его зажимах поддерживается только при вращении ротора, что требует дополнительной мощности на компенсацию механических потерь, потерь в стали магнитопровода и электрических потерь в обмотке возбуждения (в случае электромагнитного возбуждения). Эту мощность ∆Р называют потерями холостого хода. Она отбирается от двигателя, приводящего в движение генератор, и должна учитываться в мощности источника. Тогда выражение для КПД примет вид:
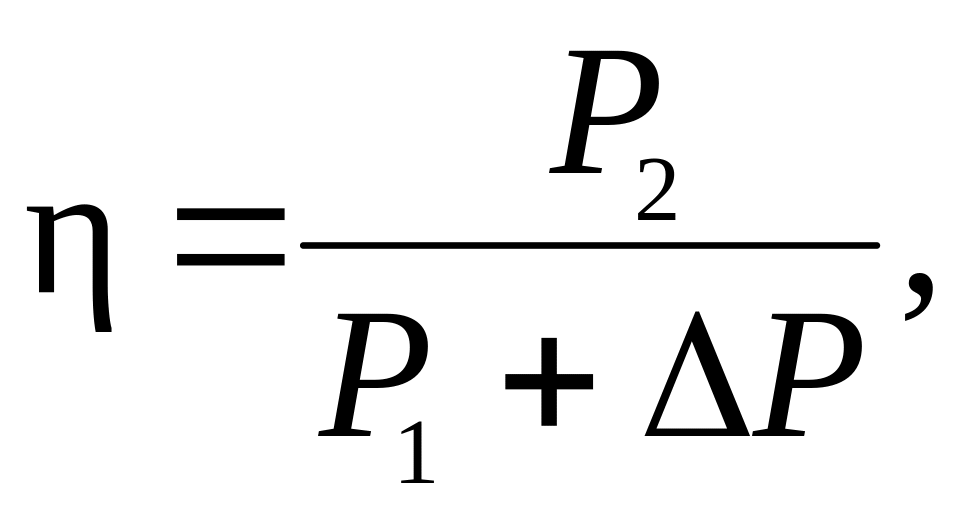
где Р1− электрическая мощность источника, отдаваемая во внешнюю цепь.
Поскольку ∆Р ≠ 0, то в режиме холостого хода Р1= 0, Р2= 0 и η= 0.
В рассмотренной выше модели линии передачи потери холостого хода не учитывались, т.к. рассматривался идеальный источник ЭДС, что и определило линейное изменение КПД.
Вид кривой КПД в реальной системе передачи показан на рис.1.7,б, где пунктирной линией показана зависимость КПД в модели линии передачи. Ввиду нелинейности зависимостей мощности в линии и нагрузке от тока наиболее экономичный режим (максимум КПД) сдвинут в область малых токов.
Согласованный режим целесообразен в системах передачи информации, где для повышения помехоустойчивости важна передача максимальной мощности полезного сигнала, а КПД не играет роли ввиду малой величины абсолютной мощности.
Напряжение на
зажимах нагрузки U2
будет
меньше напряжения генератора U1
на величину
падения напряжения UЛ
= IRЛ.
Это падение напряжения называется
потерей напряжения. Оно может быть
оценено величиной
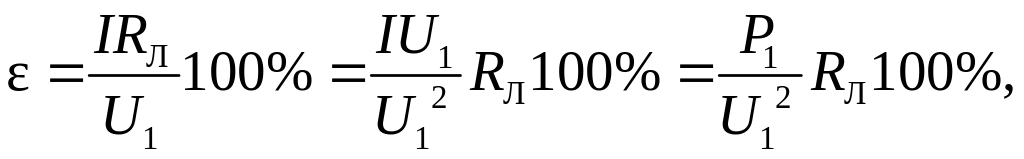 откуда следует важный вывод: при
передаче заданной мощности потеря
напряжения обратно пропорциональна
квадрату напряжения источника.
В линиях передач изменение напряжения
ε в линии не должно быть велико, так как
в противном случае напряжение на нагрузке
снижается, и не обеспечивается нормальный
режим работы приемников: лампы слабо
светятся, нагруженные электродвигатели
перегреваются и т.п. Именно поэтому
передача больших мощностей на дальние
расстояния осуществляется по линиям
высокого напряжения.
откуда следует важный вывод: при
передаче заданной мощности потеря
напряжения обратно пропорциональна
квадрату напряжения источника.
В линиях передач изменение напряжения
ε в линии не должно быть велико, так как
в противном случае напряжение на нагрузке
снижается, и не обеспечивается нормальный
режим работы приемников: лампы слабо
светятся, нагруженные электродвигатели
перегреваются и т.п. Именно поэтому
передача больших мощностей на дальние
расстояния осуществляется по линиям
высокого напряжения.


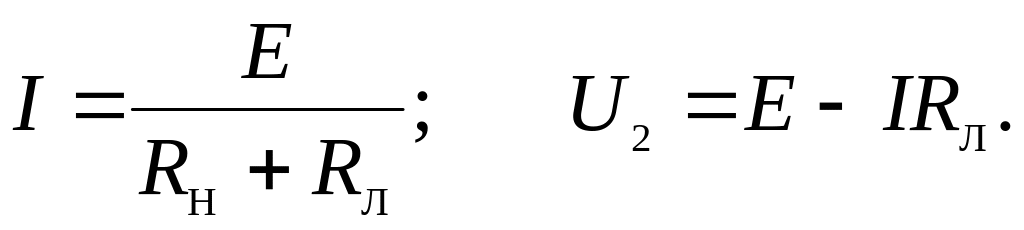 (1.14)
(1.14)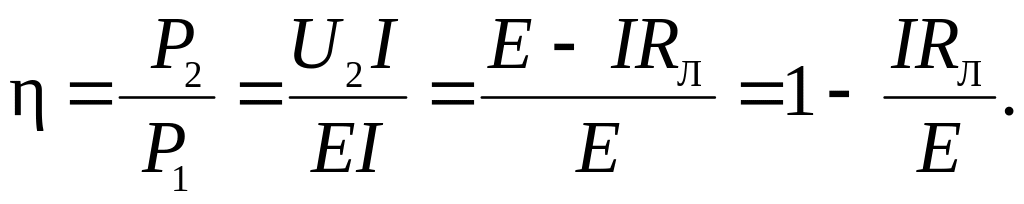 (1.15)
(1.15)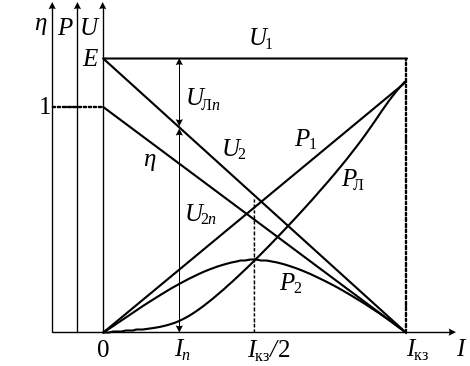 а)
а)
 б)
б)