1.1.2. Законы Кирхгофа
При расчете и анализе электрических цепей изначально необходимо задаться положительным направлением токов в ветвях. В соответствии с принятыми положительными направлениями токов определяются и положительные направления напряжений на элементах цепи. В общем случае положительные направления токов задаются произвольно. Если в результате расчета получается отрицательное значение тока, то это значит, что данный ток в ветви направлен в противоположную сторону по сравнению с принятым положительным направлением.
Электрические цепи подразделяются на неразветвленные и разветвленные. В неразветвленной цепи во всех элементах течет один и тот же ток. В разветвленной цепи по каждой ветви течет свой ток.
Все электрические цепи подчиняются законам Кирхгофа. Их два.
Первый закон - закон токов Кирхгофа (ЗТК) устанавливает связь между токами в узле электрической схемы: алгебраическая сумма токов в любом узле равна нулю, т.е.
(1.6)
При составлении уравнения (1.6) по первому закону Кирхгофа токи, направленные к узлу, следует брать со знаком, противоположным знаку токов, направленных от узла.
Второй закон - закон напряжений Кирхгофа (ЗНК) устанавливает связь между напряжениями в контуре электрической цепи: алгебраическая сумма напряжений на всех элементах вдоль любого контура равна нулю, т.е.
(1.7)
В выражении (1.7) падения напряжения, совпадающие с направлением обхода контура, берутся со знаком "плюс", а ЭДС, совпадающие с направлением обхода контура, − со знаком "минус", например, как в выражении (1.3), поскольку напряжение на источнике ЭДС направлено встречно самой ЭДС (в соответствии с направлением стрелки Е).
Для того, чтобы исключить возможные ошибки при определении знаков слагаемых в (1.7), все ЭДС из левой части уравнения целесообразно перенести в правую часть. Тогда второй закон Кирхгофа может быть сформулирован иначе: алгебраическая сумма падений напряжения в любом контуре равняется алгебраической сумме ЭДС, действующих в том же контуре, т.е.
(1.8)
В этом случае в каждую из сумм в уравнении (1.8) соответствующие слагаемые (как падения напряжения в левой части, так и ЭДС в правой) входят со знаком "плюс", если совпадают с направлением обхода контура, и со знаком "минус", если не совпадают с ним.
1.1.3. Потенциальная диаграмма
Для экспериментального подтверждения и наглядной иллюстрации второго закона Кирхгофа построим потенциальную диаграмму, которая представляет собой график распределения потенциала вдоль какого-либо участка цепи или контура. По оси абсцисс на нем откладывают в масштабе отрезки, соответствующие сопротивлениям вдоль контура, начиная с какой-либо произвольной точки, а по оси ординат − потенциалы соответствующих точек контура относительно точки, потенциал которой принят за нулевой.
Рассмотрим контур электрической цепи, изображенный на рис.1.3, и построим для него потенциальную диаграмму. Для этого зададим направление обхода контура по часовой стрелке и примем потенциал точки a равным нулю: φa= 0.
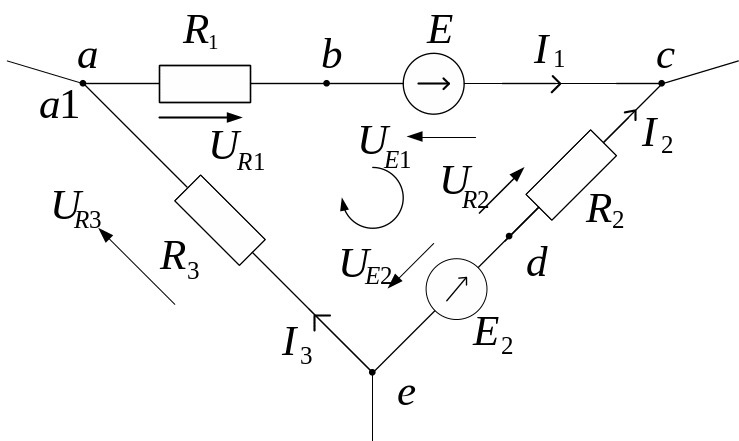
Рис. 1.3. Контур электрической цепи
Для потенциалов соответствующих точек схемы согласно выражениям (1.1)...(1.4) справедливы следующие соотношения:
φb= φa−I1R1= − I1R1;
φc= φb +E1 = − I1R1+ E1;
φd= φc + I2R2 = − I1R1+ E1 + I2R2;
φe= φd − E2 = − I1R1+ E1 + I2R2 − E2;
φa1= φe − I3R3 = − I1R1+ E1 + I2R2 − E2 −I3R3,
где φa1 - потенциал точки a, выраженный через напряжения на элементах контура.
Обходя контур по часовой стрелке, мы пришли в ту же точку a (a1), из которой начали движение. Разность потенциалов φa и φa1, очевидно, равна нулю, т.е.
φa− φa1 = I1R1−E1 − I2R2 + E2 +I3R3=0. (1.9)
В обозначениях напряжений на элементах контура выражение (1.9) принимает вид:
(1.10)
что соответствует уравнению (1.7) для ЗНК.
Перенеся ЭДС в правую часть равенства (1.9), получим:
I1R1− I2R2 +I3R3 = E1− E2, (1.11)
что соответствует уравнению (1.8) для ЗНК.
Потенциальная диаграмма в виде зависимости φ(R) приведена на рис.1.4. Пользуясь потенциальной диаграммой, можно найти разность потенциалов между любыми точками электрической цепи.
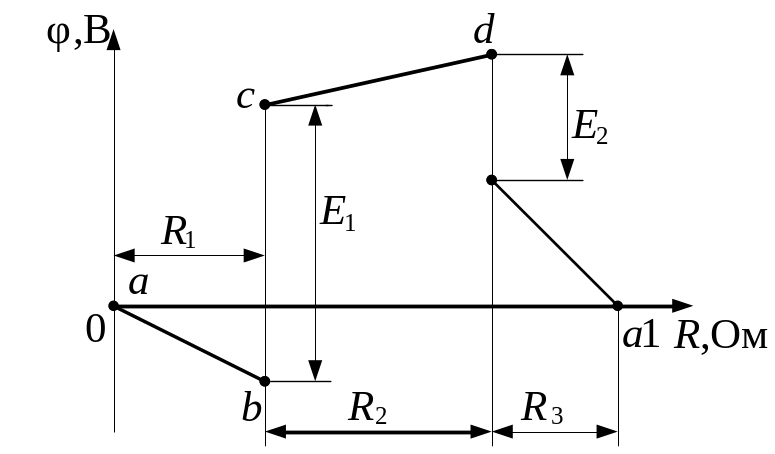
Рис.1.4. Потенциальная диаграмма
Правильность расчета электрической цепи можно проверить по балансу мощности, согласно которому суммарная мощность, генерируемая источниками, равна суммарной мощности, потребляемой в цепи:
(1.12)
где k − количество источников ЭДС в схеме; n − количество приемников (активных сопротивлений).