6.2.5. Расчетная часть
1. Для переходных режимов в цепи RC
Рассчитать для осциллограммы №1 постоянную времени и сравнить с опытной. Построить кривую напряжения на конденсаторе ёмкостью 8мкФ при подключении его на напряжение U=2В через сопротивление R=200 Ом. Сравнить полученную кривую с осциллограммой №1.
2.Для переходных режимов в цепи RL
Рассчитать по параметрам цепи для осциллограммы №1 постоянную времени τ и построить кривые тока и напряжения на индуктивности при подключении цепи к источнику постоянного напряжения 2 В. Сравнить с осциллограммами №1 и №4.
3.Для переходных режимов в цепи RLC второго порядка
Рассчитать для каждой осциллограммы по формуле (6,35) критическое сопротивление Rкр. Проверить соответствие полученных величин сопротивлений характеру переходного процесса.
Рассчитать по параметрам цепи осциллограммы №2, используя формулу (6,36), период колебаний Т и сравнить его с полученным из опыта.
6.2.6. Содержание отчета
1 Титульный лист.
2. Цель и краткое содержание работы.
3. Схемы испытаний исследуемых цепей.
4 .Таблицы с данными испытаний и расчетов.
5. Произведённые расчёты и построения.
6. Осциллограммы кривых токов и напряжений.
7. Ответы на контрольные вопросы
6.2.7. Контрольные вопросы
1. Что подразумевается под переходным процессом в электрических цепях, и в чём причина его возникновения?
2. Какой вид функции времени описывает переходный процесс в линейных цепях? Какие коэффициенты этой функции необходимо определять для описания конкретного переходного процесса?
3. Что такое законы коммутации, чем они обусловлены, и как их используют для определения начальных условий?
4. Что такое постоянная времени τ в цепи первого порядка, как её измерить на осциллограмме?
5. Чем определяется характер переходного процесса в цепи второго порядка: апериодический или колебательный?
6. Как по параметрам цепи определить приближенно длительность переходного процесса в цепях первого и второго порядка?
Раздел 7. Электрические цепи
С НЕЛИНЕЙНЫМИ РЕЗИСТИВНЫМИ ЭЛЕМЕНТАМИ
7.1. Краткие теоретические сведения
7.1.1. Основные понятия и определения
Нелинейными электрическими элементами называются такие элементы, параметры которых зависят от тока и напряжения. Нелинейные цепи − это цепи, содержащие один или несколько нелинейных элементов.
Простейшим примером нелинейного элемента является нить накала электрической лампочки. При протекании по ней электрического тока температура нити растет, что приводит к увеличению активного сопротивления. При этом, чем больше ток, тем больше выделяется тепла и тем больше сопротивление. Соответственно зависимость падения напряжения на таком элементе от тока (его вольт-амперная характеристика) выражается нелинейной функцией.
Нелинейные элементы можно разделить на две группы: симметричные и несимметричные.
Симметричные нелинейные элементы обладают вольт-амперной характеристикой, вид которой не зависит от направления тока в них и напряжения на зажимах.
Несимметричные нелинейные элементы имеют неодинаковые вольт-амперные характеристики при различных направлениях тока в них и напряжения на зажимах.
При расчете цепей с нелинейными резистивными элементами вводят понятия статического и дифференциального (динамического) сопротивлений. Для их определения рассмотрим вольт-амперную характеристику нелинейного элемента, изображенную на рис. 7.1.
Рис. 7.1. Вольт-амперная характеристика нелинейного
резистивного элемента
Статическое сопротивление в точке a характеристики определяется как отношение напряжения Ua к току Ia:
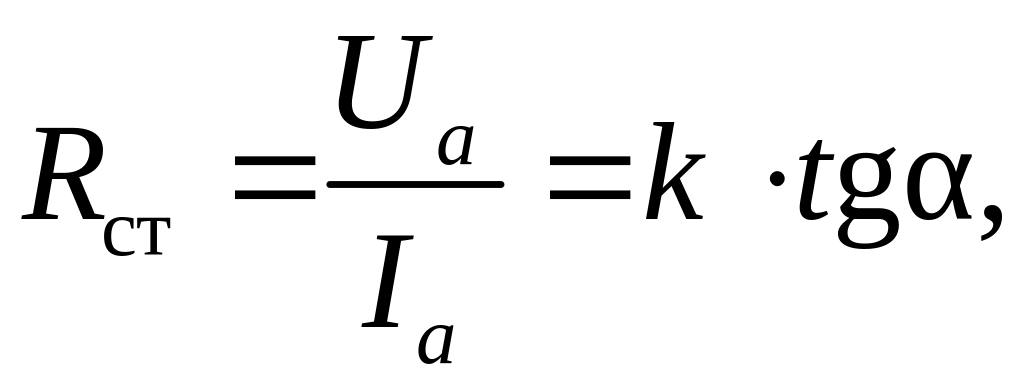
где k− коэффициент, равный отношению масштабов напряжения и тока по осям координат. Как видно из рисунка, статическое сопротивление пропорционально тангенсу угла между секущей 0a и осью абсцисс. Оно характеризует работу нелинейного элемента в установившемся режиме.
При изменении тока в окрестности точки a, т.е. в динамическом режиме, сопротивление нелинейного элемента определяется как отношение приращения напряжения к приращению тока, в пределе давая производную:
где k− коэффициент, равный отношению масштабов напряжения и тока по осям координат. Как видно из рисунка, динамическое сопротивление пропорционально тангенсу угла между касательной к вольт-амперной характеристике в точке a и осью абсцисс.
Статическое и динамическое сопротивление изменяется от точки к точке вольт-амперной характеристики нелинейного элемента. При этом статическое сопротивление всегда положительно, в то время как динамическое может принимать отрицательные значения. Это определяется наклоном вольт-амперной характеристики: если характеристика содержит нисходящие участки, то Rд˂0.
В лабораторной работе, посвященной исследованию нелинейных цепей, используются несимметричные нелинейные резистивные элементы, поэтому остановимся лишь на тех резистивных элементах, которые являются объектом исследования.