6.1.4. Расчет переходного процесса
в цепях первого порядка
Рассмотрим расчет переходного процесса в цепях с индуктивностью и с емкостью.
1. Цепь, содержащая элементы R,L
Расчетная схема приведена на рис. 6.5. Коммутация происходит замыканием ключа К.
Рис. 6.5. Расчетная схема с R,L элементами
Составляем уравнение по ЗНК для цепи после коммутации (ключ К замкнут) в соответствии с принятыми положительными направлениями тока и падений напряжения:
uL(t) + uR(t) = E.
Переменным состояния, которое определяет поведение цепи в переходном процессе, является ток в индуктивности. Относительно него и запишем уравнение.
Выражая падения напряжения uL(t) и uR(t) через ток iL(t) в цепи, получим дифференциальное уравнение первого порядка
(6.17)
Характеристическое уравнение имеет вид:
Величина L/R имеет размерность времени (с), называется постоянной времени и обозначается через τ.
Находим корень характеристического уравнения:
В соответствии с (6.9) решением уравнения (6.17) будет
Согласно табл. 6.2 установившееся и начальное значения тока в индуктивности: ILуст= E/R, iL+0 = 0.
Для момента времени t= t+0=0 можно записать:
откуда находим произвольную постоянную С:
С= iL+0− ILуст=− ILуст= −E/R.
Соответственно решение уравнения (6.17) :
(6.18)
Проанализируем полученный результат.
Первое слагаемое
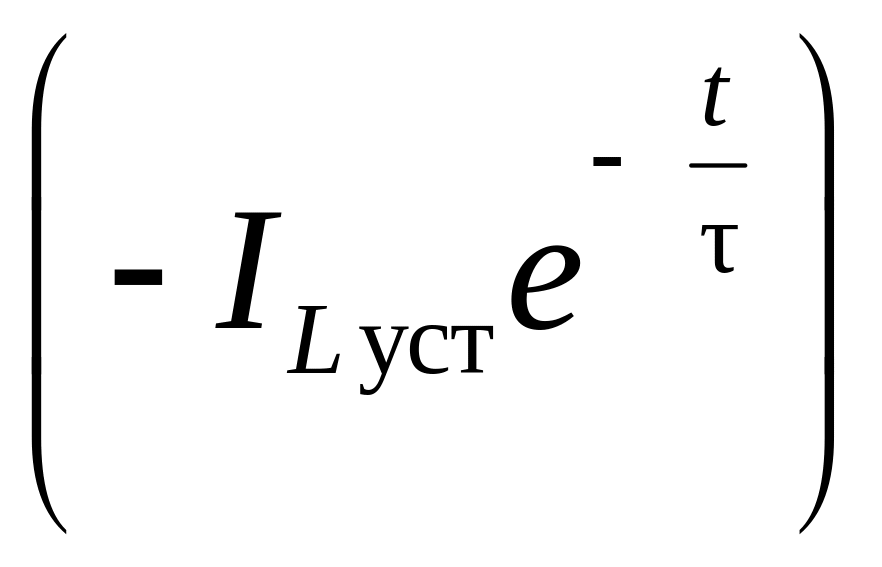в (6.18) представляет собой общее решение
iобщ(t)
исходного дифференциального уравнения.
При t→∞
оно стремится
к нулю. Это значит, что оно характеризует
переходный режим, затухающий с течением
времени.
В теории переходных процессов общее решение уравнения, описывающего переходный процесс, называют свободной составляющей и обозначают iLсв(t). Физически стремление к нулю свободной составляющей обусловлено наличием в цепи активного сопротивления, в котором имеют место необратимые потери энергии. Таким образом, с учетом принятых обозначений решение уравнения (6.17) имеет вид:
(6.19)
Именно в таких обозначениях будем искать решение и в дальнейшем.
Теперь выясним физический смысл постоянной времени τ.
Рассмотрим интервал ∆t=τ и найдем, как изменяется свободная составляющая iLсв(t) за данный промежуток времени. Для этого найдем отношение iLсв(t+τ)/ iLсв(t):
Полученный результат означает, что за интервал времени, равный постоянной времени цепи, свободная составляющая уменьшается в e раз.
С использованием (6.19) найдем, как изменяется напряжение на индуктивности в переходном процессе:
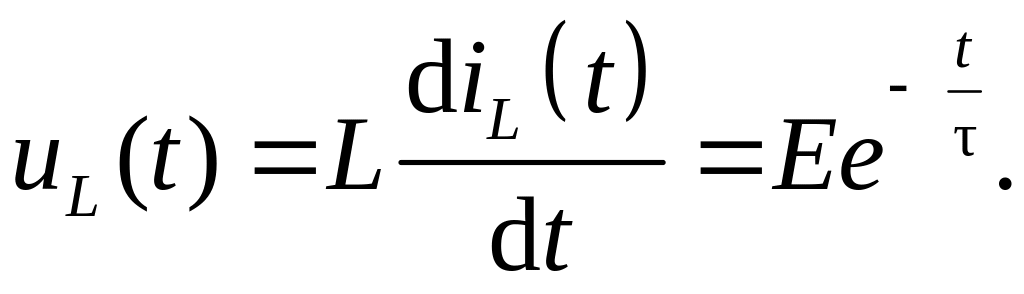(6.20)
На рис. 6.6 приведены кривые изменения тока (а) и напряжения (б) на индуктивности в переходном режиме, построенные по выражениям (6.19) и (6.20).
а) б)
Рис. 6.6. Кривые тока (а) и напряжения (б) на индуктивности
в переходном процессе
Кривая тока iL(t) является результатом от сложения кривых свободной составляющей iLсв(t) и установившегося режима ILуст. Как видно из графиков, ток iL(t) в индуктивности изменяется от значения, которое он имел до коммутации, а напряжение uL(t) в момент коммутации претерпевает скачок.
Отметим без доказательства, что проведенная в любой точке кривой переходного процесса касательная дает значение подкасательной, равное постоянной времени τ цепи. Данный факт позволяет по величине τ оценить время переходного процесса. Строго говоря, переходный процесс заканчивается в бесконечности. Но можно считать, что установившийся режим наступает в течение времени, равного (4...5)τ. Таким образом, если постоянная времени может быть определена без расчета переходного режима, то можно оценить время переходного процесса, зная параметры цепи.
Рассмотрим переходный процесс в той же цепи, но при отключении ее от источника. Расчетная схема приведена на рис. 6.7.
Рис. 6.7. Расчетная схема цепи
Ключ К отключает цепь от источника и замыкает ее накоротко перемычкой. До коммутации направление тока iL(t) в цепи обозначено стрелкой. В момент коммутации согласно закону коммутации ток ни по величине, ни по направлению не изменился. Составим уравнения по ЗНК для цепи после коммутации и решим его.
uL(t) + uR(t) = 0.
Выражая падения напряжения uL(t) и uR(t) через ток iL(t) в цепи, получим дифференциальное уравнение первого порядка
(6.21)
Характеристическое уравнение имеет вид:
Находим корень характеристического уравнения:
где τ=L/R − постоянная времени цепи.
В соответствии с (6.9) решением уравнения (6.21) будет
Согласно табл. 6.2 установившееся и начальное значения тока в индуктивности: ILуст= 0, iL+0 = E/R.
Для момента времени t= t+0=0 можно записать:
откуда находим произвольную постоянную С:
С= iL+0− ILуст= iL+0 = E/R.
Соответственно решение уравнения (6.17) :
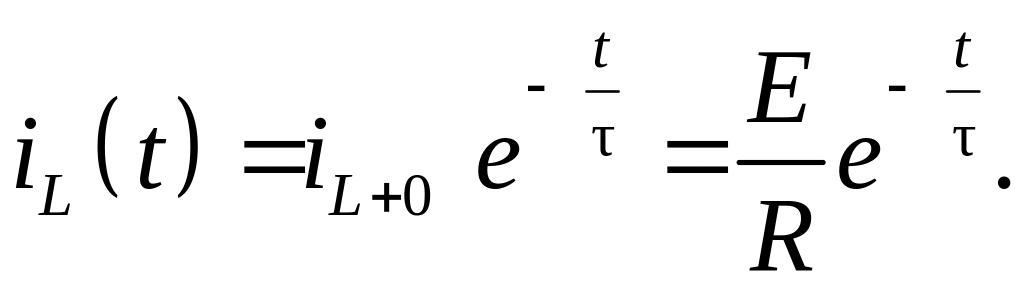(6.22)
Напряжение на индуктивности в переходном процессе:
(6.23)
На рис. 6.8 приведены кривые изменения тока (а) и напряжения (б) на индуктивности в переходном режиме, построенные по выражениям (6.22) и (6.23).
а) б)
Рис. 6.8. Кривые тока (а) и напряжения (б) на индуктивности
в переходном процессе
Напряжение на индуктивности по величине в момент коммутации скачкообразно изменяется от нуля до E, а затем по экспоненциальному закону уменьшается до нуля.
Поскольку за время, равное постоянной времени, ток и напряжение уменьшаются в e раз, то по кривой переходного процесса, например, тока можно легко найти величину постоянной времени. Действительно, для t=τ значение ординаты iτ кривой тока будет равно iτ= iL+0 /e=0,37iL+0.
Данное соотношение целесообразно использовать для нахождения постоянной времени по экспериментальным кривым переходных процессов в цепях первого порядка.
2. Цепь, содержащая элементы R,С
Расчетная схема приведена на рис. 6.9. Коммутация происходит замыканием ключа К.
Рис. 6.9. Расчетная схема с R,С элементами
Составляем уравнение по ЗНК для цепи после коммутации (ключ К замкнут) в соответствии с принятыми положительными направлениями тока iС(t) и падений напряжения на емкости uС(t) и на активном сопротивлении uR(t) :
uС(t) + uR(t) = E.
Переменным
состояния, которое определяет поведение
цепи в переходном процессе, является
напряжение на емкости
uС(t).
Относительно него и запишем уравнение,
полагая
(6.24)
Характеристическое уравнение имеет вид:
где τ=RC − постоянная времени цепи, имеющая размерность времени (с).
Находим корень характеристического уравнения:
В соответствии с (6.9) решением уравнения (6.24) будет
где UCуст − установившееся значение напряжения на емкости после коммутации.
Согласно табл. 6.2 установившееся и начальное значения напряжения на индуктивности: UCуст= E, uС+0 = 0.
Для момента времени t= t+0=0 можно записать:
откуда находим произвольную постоянную С:
С= uC+0− UCуст=− UCуст= E.
Соответственно решение уравнения (6.24) :
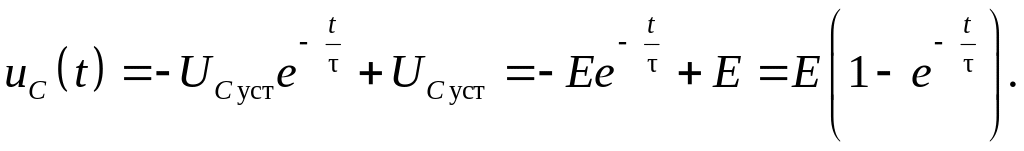(6.25)
Ток в емкости в переходном процессе:
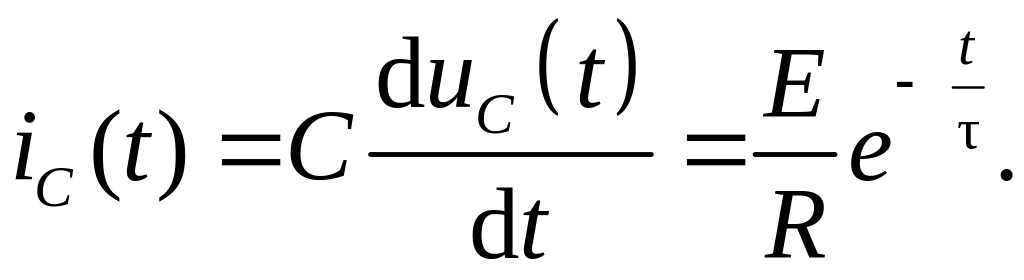(6.26)
На рис. 6.10 приведены кривые изменения напряжения (а) и тока (б) в емкости в переходном режиме, построенные по выражениям (6.24) и (6.25).
а) б)
Рис. 6.10. Кривые напряжения (а) и тока (б) в емкости
в переходном процессе
Кривая напряжения uС(t) является результатом от сложения кривых свободной составляющей uCсв(t) и установившегося режима UCуст. Как видно из графиков, напряжение uС(t) в емкости изменяется от значения, которое оно имело до коммутации, а ток iC(t) в момент коммутации претерпевает скачок.
Рассмотрим переходный процесс в той же цепи, но при отключении ее от источника. Расчетная схема приведена на рис. 6.11.
Ключ К отключает цепь от источника и замыкает ее накоротко перемычкой.
Рис. 6.11. Расчетная схема цепи
До коммутации направление напряжения uС(t) в цепи обозначено стрелкой. В момент коммутации согласно закону коммутации напряжение ни по величине, ни по направлению не изменилось. Примем направление падения напряжения uR(t) на активном сопротивлении, как на рис. 6.11, и составим уравнение ЗНК:
uС(t) + uR(t) = 0.
Студентам предлагается самостоятельно решить данное уравнение и построить соответствующие графики. Запишем лишь окончательное решение:
Ток в емкости в переходном процессе
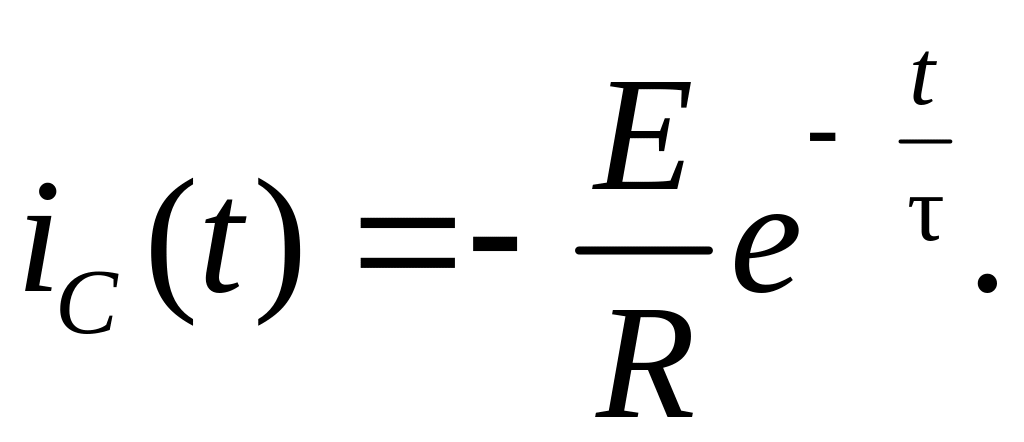
Знак минус в выражении для тока в емкости означает, что направление его противоположно принятому положительному направлению напряжений на рис. 6.11, т.е. физически происходит процесс разряда емкости.