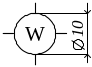- •Раздел 1. Линейные цепи постоянного тока
- •1.1. Краткие теоретические сведения
- •1.2.Лабораторная работа №1. Исследование резистивной цепи
- •1.3. Лабораторная работа №2. Исследование линии передачи
- •Раздел 2. Пассивные двухполюсники
- •Раздел 3. Трехфазные цепи
- •Раздел 4. Индуктивно − связанные цепи
- •Раздел 5. Линейные цепи периодического
- •5.1. Краткие теоретические сведения
- •5.2. Лабораторная работа №9. Линейные цепи периодического
- •Раздел 6. Переходные процессы в линейных
- •6.1. Краткие теоретические сведения
- •6.2. Лабораторная работа №10. Переходные процессы в линейных
- •Раздел 7. Электрические цепи
- •7.1. Краткие теоретические сведения
- •7.2. Лабораторная работа №11. Исследование цепей
- •В.1. Правила внутреннего распорядка и техники безопасности при выполнении лабораторных работ
- •В.2. Общие методические рекомендации и указания по выполнению лабораторных работ
- •В.3. Условные графические обозначения элементов электрических схем
- •Раздел 1. Линейные цепи постоянного тока
- •1.1. Краткие теоретические сведения
- •1.1.1. Основные понятия и определения
- •1.1.2. Законы Кирхгофа
- •1.1.3. Потенциальная диаграмма
- •1.1.4. Метод наложения
- •1.1.5. Линия передачи
- •1.2. Лабораторная работа №1
- •1.2.1. Цель и краткое содержание работы
- •1.2.3. Порядок выполнения измерений
- •1.2.4. Расчетная часть
- •1.2.5. Содержание отчета
- •1.2.6. Контрольные вопросы
- •1.3. Лабораторная работа №2
- •1.3.1. Цель и краткое содержание работы
- •1.1.1. Основные понятия и определения;
- •1.1.5. Линия передачи.
- •1.3.2. Описание лабораторного стенда
- •1. Напряжение на входе схемы устанавливать не более 20 в.
- •2. Избегать работы схемы при токах нагрузки более 0,3 а на протяжении более 10 мин.
- •1.3.3. Порядок выполнения измерений
- •1.3.4. Расчетная часть
- •1.3.5. Содержание отчета
- •1.3.6. Контрольные вопросы
- •Раздел 2. Пассивные двухполюсники
- •2.1. Краткие теоретические сведения
- •2.1.1. Основные понятия и определения
- •2.1.2. Основы символического метода
- •2.1.3. Комплексное представление элементов электрической цепи
- •2.1.4. Расчет цепей гармонического тока
- •2.1.5. Мощность в цепи гармонического тока
- •2.1.6. Резонанс в цепи гармонического тока
- •2.2. Лабораторная работа №3
- •2.2.1. Цель и краткое содержание работы
- •2.2.3. Порядок выполнения измерений
- •2.2.4. Расчетная часть
- •2.2.5. Содержание отчета
- •2.2.6. Контрольные вопросы
- •2.3. Лабораторная работа №4
- •2.3.1. Цель и краткое содержание работы
- •2.3.4. Расчетная часть
- •2.3.5. Содержание отчета
- •2.3.6. Контрольные вопросы
- •2.4. Лабораторная работа №5
- •2.4.1. Цель и краткое содержание работы
- •2.1.4. Расчет цепей гармонического тока;
- •2.1.5. Мощность в цепи гармонического тока;
- •2.1.6. Резонанс в цепи гармонического тока.
- •2.4.2. Описание лабораторного стенда
- •2.4.3. Порядок выполнения измерений
- •2.4.4. Расчетная часть
- •2.4.5. Содержание отчета
- •2.4.6. Контрольные вопросы
- •Раздел 3. Трехфазные цепи
- •3.1. Краткие теоретические сведения
- •3.1.1. Основные понятия и определения
- •3.1.2. Схемы соединения трехфазных цепей
- •3.1.3. Расчет трехфазных цепей
- •3.1.4. Мощность в трехфазной цепи
- •3.2. Лабораторная работа №6
- •3.2.1. Цель и краткое содержание работы
- •3.2.3. Порядок выполнения измерений
- •3.2.4. Расчетная часть
- •3.2.5. Содержание отчета
- •3.2.6. Контрольные вопросы
- •3.3. Лабораторная работа №7
- •3.3.1. Цель и краткое содержание работы
- •3.3.3. Порядок выполнения измерений
- •3.3.4. Расчетная часть
- •3.3.5. Содержание отчета
- •3.3.6. Контрольные вопросы
- •Раздел 4. Индуктивно − связанные цепи
- •4.1. Краткие теоретические сведения
- •4.1.1. Основные понятия и определения
- •4.1.2. Расчет электрических цепей
- •4.1.3. Определение одноименных зажимов
- •4.1.4. Экспериментальное определение
- •4.2. Лабораторная работа №8
- •4.2.1. Цель и краткое содержание работы
- •4.2.3. Порядок выполнения измерений
- •4.2.4. Расчетная часть
- •4.2.5. Содержание отчета
- •4.2.6. Контрольные вопросы
- •Раздел 5. Линейные цепи периодического
- •5.1. Краткие теоретические сведения
- •5.1.1. Основные понятия и определения
- •5.1.2. Расчет цепей негармонического тока
- •5.2. Лабораторная работа №9
- •5.2.1. Цель и краткое содержание работы
- •5.1.1. Основные понятия и определения;
- •5.1.2. Расчет цепей негармонического тока.
- •5.2.2. Описание лабораторного стенда
- •5.2.3. Работа с портативным осциллографом hps-1401
- •5.2.4. Порядок выполнения измерений
- •5.2.5. Расчетная часть
- •5.2.6. Содержание отчета
- •5.2.7. Контрольные вопросы
- •Раздел 6. Переходные процессы в линейных
- •6.1. Краткие теоретические сведения
- •6.1.1. Понятие переходного процесса.
- •6.1.2. Сведения из теории линейных
- •6.1.3. Расчет начальных условий
- •6.1.4. Расчет переходного процесса
- •6.1.5. Расчет переходного процесса
- •6.1.6. Порядок расчета переходных процессов
- •6.2. Лабораторная работа №10
- •6.2.1. Цель и краткое содержание работы
- •6.2.3. Работа с портативным осциллографом hps-1401
- •6.2.4. Порядок выполнения измерений
- •6.2.5. Расчетная часть
- •6.2.6. Содержание отчета
- •6.2.7. Контрольные вопросы
- •Раздел 7. Электрические цепи
- •7.1. Краткие теоретические сведения
- •7.1.1. Основные понятия и определения
- •7.1.2. Полупроводниковый диод
- •7.1.3. Полупроводниковый стабилитрон
- •7.1.4. Динистор
- •7.2. Лабораторная работа №11
- •7.2.1. Цель и краткое содержание работы
- •7.2.3. Порядок выполнения измерений
- •7.2.4. Расчетная часть
- •7.2.5. Содержание отчета
- •7.2.6. Контрольные вопросы
В.3. Условные графические обозначения элементов электрических схем
Под электрической цепью понимают совокупность связанных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. Изображение электрической цепи с помощью условных знаков называют электрической схемой. Изображения различных элементов в электрических схемах приведены в таблице.
Название |
Обозначение |
Название |
Обозначение |
Резистор |
|
Переменный резистор |
|
Катушка индуктивности |
|
Конденсатор |
|
Источник ЭДС |
|
Источник тока |
|
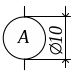
Амперметр |
|
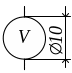
Вольтметр |
|
Ваттметр |
|
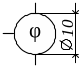
Фазометр |
|
Если число выводов, с помощью которых элемент присоединяется к электрической цепи, равно двум, то такой элемент называется двухполюсником. Если таких выводов четыре, то - четырехполюсником. В данном лабораторном практикуме рассматриваются двухполюсники.
Теоретические сведения, необходимые для выполнения лабораторного практикума, изложены в соответствующих разделах настоящего пособия. Более подробные теоретические сведения изложены в [1-4].
Раздел 1. Линейные цепи постоянного тока
1.1. Краткие теоретические сведения
1.1.1. Основные понятия и определения
Постоянным током называют ток, неизменный во времени. Источник электрической энергии характеризуется величиной и направлением электродвижущей силы (ЭДС) и величиной внутреннего сопротивления.
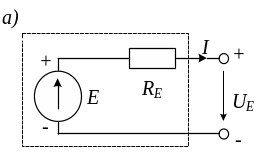
Напомним, что при расчете и анализе электрических цепей источник электрической энергии может быть представлен одной из моделей (рис.1.1):
- в виде идеального источника ЭДС E с последовательно включенным сопротивлением, равным внутреннему сопротивлению RE реального источника,
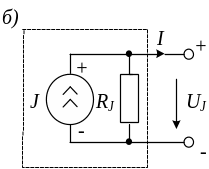
- в виде идеального источника тока J с параллельно включенным с ним сопротивлением, равным внутреннему сопротивлению RJ реального источника.
|
|
Рис.1.1. Источники: а – ЭДС, б – тока.
|
|
Известно правило эквивалентной замены одного источника другим:
E = JRJ и RJ =RE ,
где E - ЭДС источника напряжения, J - ток источника тока, RE и RJ - их внутренние сопротивления. Для электрической цепи не принципиально, какая модель принята, поскольку возможна эквивалентная замена одного источника другим. Поэтому в дальнейшем мы будем пользоваться источником ЭДС E с последовательно включенным внутренним сопротивлением RE .
В условном изображении источника ЭДС стрелка указывает на направление возрастания потенциала внутри источника, т.е. на положительное направление ЭДС. Из курса физики известно, что потенциал, являясь энергетической характеристикой электрического поля, связан с работой по перемещению единичного заряда. Поэтому физически стрелка в обозначении ЭДС означает направление разделения зарядов внутри источника в результате работы по преодолению кулоновских сил и указывает на положительный полюс. То же самое можно сказать и об источнике тока.
Под напряжением Uab на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка:
Uab= φa− φb.
На схемах напряжение изображают стрелкой. За положительное направление принимают направление понижения потенциала, поэтому напряжение на зажимах источника UE направлено встречно направлению ЭДС E, например, как на рис.1.1. При этом численно UE = E.
Напряжение на активном сопротивлении направлено так же, как и протекающий по нему ток, поскольку ток течет в направлении понижения потенциала. Напряжение на активном сопротивлении называют падением напряжения.
Для иллюстрации сказанного рассмотрим рис.1.2 с участком цепи, содержащим активное сопротивление R и ЭДС E .
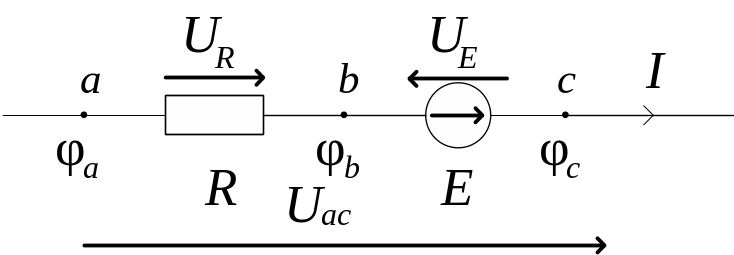
Рис.1.2. Участок цепи, содержащий ЭДС.
Напряжение между точками a и c равно разности потенциалов в соответствующих точках: Uaс= φa− φс . Падение напряжения на активном сопротивлении согласно закону Ома
UR = φa− φb = IR. (1.1)
Напряжение на источнике ЭДС
UE = φс− φb = E. (1.2)
Тогда очевидно равенство:
Uaс= UR − UE = IR − E = φa− φс. (1.3)
Следует обратить внимание на то, что в (1.3) падение напряжения на сопротивлении R и ЭДС E имеют разные знаки, хотя направлены одинаково, поскольку стрелка ЭДС указывает на повышение потенциала.
Если в данной цепи ЭДС E направлена в противоположную сторону, то последнее уравнение примет вид:
Uaс= UR + UE = IR + E = φa− φс. (1.4)
С использованием полученных выражений находим формулу для расчета тока в цепи при известных величинах Uaс , E и R:
![]() (1.5)
(1.5)
Если направления тока и ЭДС совпадают, то в числителе дроби (1.5) ставится знак "плюс", если не совпадают, то "минус". Выражение (1.5) может использоваться для расчета токов в ветвях методом узловых напряжений.