3.1.3. Расчет трехфазных цепей

Расчет трехфазных цепей ведется известными методами расчета цепей гармонического тока, т.к. они представляют собой частный случай сложной цепи, в которой действуют несколько источников ЭДС. Рассмотрим особенности расчета трехфазных цепей при соединении источников и приемников по схеме "звезда-звезда" и "треугольник-треугольник".

1. Схема "звезда-звезда"

Схема трехфазной цепи представлена на рис.3.6. Сопротивления линейных проводов включены в сопротивления фаз нагрузки. Сопротивление нулевого провода обозначено Соотношения между напряжениями в цепи устанавливаются ЗНК:

(3.5)

Напряжения являются напряжениями на зажимах генератора и равны соответствующим ЭДС. Поэтому они образуют симметричную звезду векторов (рис. 3.7). Линейные напряжения также образуют симметричную систему. На векторной диаграмме рис. 3.7 в соответствии с выражениями (3.5) изображены и остальные векторы напряжений схемы.

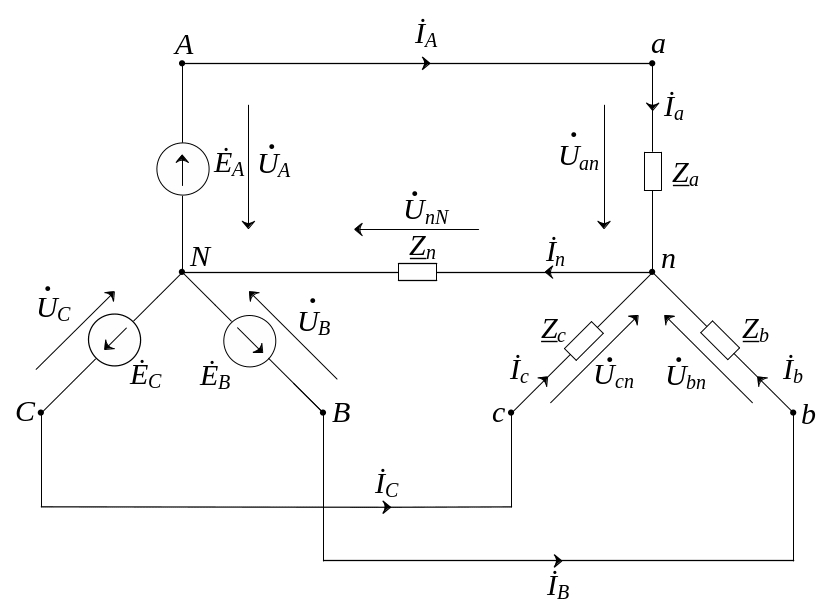
Рис. 3.6. Расчетная схема трехфазной цепи "звезда-звезда"

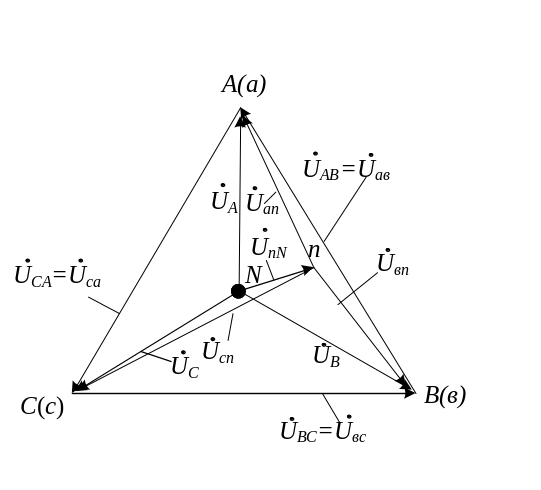
Рис. 3.7. Векторная диаграмма при несимметричной нагрузке

Величина падения напряжения в нулевом проводе зависит от параметров нагрузки, поэтому соответствующий вектор по величине и направлению на диаграмме рис. 3.7 изображен произвольно.

Как следует из векторной диаграммы, фазные напряжения на нагрузке не одинаковы и отличаются от фазных напряжений источника на величину падения напряжения в нулевом проводе . Такое положение недопустимо в реальных системах электроснабжения. Поэтому нулевой провод выполняют с минимальным сопротивлением, величиной которого можно пренебречь. Тогда падение напряжения в нулевом проводе можно считать равным нулю, и на векторной диаграмме точка n совпадет с точкой N. При этом вектора фазных напряжений совпадут с векторами фазных напряжений источника, а система станет симметричной.

Таким образом, основная роль нулевого провода − выравнивание фазных напряжений при несимметричной нагрузке фаз.

Если нулевой провод отсутствует, то векторная диаграмма при несимметричной нагрузке подобна диаграмме рис. 3.7, в которой вектор представляет собой напряжение между нейтральными точками генератора и нагрузки. Соотношения между напряжениями цепи при этом также описываются выражениями (3.5).

Рассмотрим два аварийных режима работы трехфазной цепи:

− короткое замыкание одной из фаз нагрузки;

− обрыв одной из фаз,

которые исследуются в лабораторном практикуме.

Короткое замыкание одной из фаз нагрузки, (например, фазы b)

Это означает, что сопротивление фазы стало равно нулю: .

При наличии нулевого провода такая ситуация приведет к замыканию накоротко фазы В источника, что, в свою очередь, приведет к срабатыванию автомата защиты в данной фазе. В других же фазах ничего не изменится, т.к. их фазные напряжения не изменились. Ток в нулевом проводе станет равен сумме токов фаз А и С .

В том случае, когда нулевой провод отсутствует, замыкание в фазе b приведет к изменению фазных напряжений. Схема цепи при замыкании фазы b приведена на рис. 3.8.

Из схемы видно, что для принятых положительных направлениях напряжений имеют место соотношения:

Векторная диаграмма, соответствующая данному режиму, приведена на рис. 3.9. Звезда фазных и треугольник линейных напряжений источника образуют соответственно симметричную звезду и треугольник, в то время как звезда фазных напряжений приемника изменилась.

Рис. 3.8. Схема цепи при коротком замыкании фазы b

Рис. 3.9. Векторная диаграмма при коротком замыкании фазы b

По сравнению с диаграммой рис. 3.7 произошли следующие изменения:

− точка n совместилась c точкой B(b) , т.к. а звезда фазных ЭДС источника не изменилась;

− фазные напряжения неповрежденных фаз совпали по величине с линейными напряжениями;

− напряжение стало равно напряжению закороченной фазы.

Если повышение фазного напряжения и соответственно тока в нагрузке в раз недопустимо по условиям эксплуатации, то в случае замыкания накоротко одной из фаз сработают аварийные выключатели.

Обрыв одной из фаз нагрузки, например, фазы b

При наличии нулевого провода в фазах А и С ничего не произойдет, т.к. фазные напряжения в нагрузке останутся прежними. Ток же в нулевом проводе станет равным сумме токов фаз А и С.

Схема цепи без нулевого провода приведена на рис. 3.10. Рассмотрим случай чисто активной симметричной нагрузки.

Рис. 3.10.Схема цепи при обрыве фазы b

Фазы a и c нагрузки (сопротивления R_a и R_b) оказываются соединенными последовательно, и к ним прикладывается линейное напряжение В соответствии с ЗНК согласно принятым положительным направлениям оно уравновешивается фазными напряжениями

Поскольку нагрузка фаз активная и симметричная, фазные напряжения будут одинаковыми по величине, а вектора, их изображающие, и вектор линейного напряжения будут параллельны. Векторная диаграмма при этом примет вид, как на рис. 3.11.

Звезда фазных и треугольник линейных напряжений источника останутся без изменения, поскольку они определяются источником, в то время как фазные напряжения нагрузки изменились, и появилось напряжение .

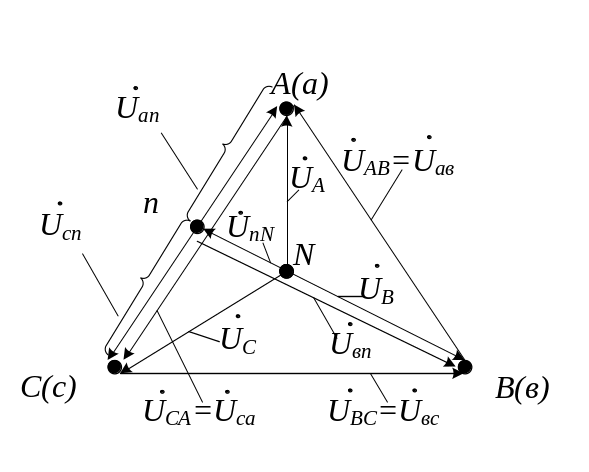
Рис. 3.11. Векторная диаграмма цепи при обрыве фазы b

По сравнению с диаграммой рис. 3.7 здесь произошли следующие изменения:

− точка n заняла серединное положение на векторе линейного напряжения при этом фазные напряжения по величине равны половине линейного напряжения;

− напряжение на разомкнутой фазе возросло (в данном случае в 1,5 раза);

− напряжение в данном случае по величине равно половине фазного напряжения источника.

Таким образом, рассмотрение несимметричных режимов показывает, что отсутствие нулевого провода в аварийных режимах приводит к существенному перекосу фазных напряжений по сравнению с симметричным режимом.

Расчет симметричного режима несложен. Поскольку система симметрична, то напряжение между нейтральными точками и ток в нулевом проводе равны нулю, а фазные напряжения на нагрузке равны соответствующим фазным напряжениям источника. Тогда токи в фазах найдутся по выражениям:

(3.6)

Несимметричный режим цепи с нулевым проводом конечного сопротивления целесообразно вести по методу узловых напряжений.

Если в качестве нулевого принять потенциал узла N, то можно записать

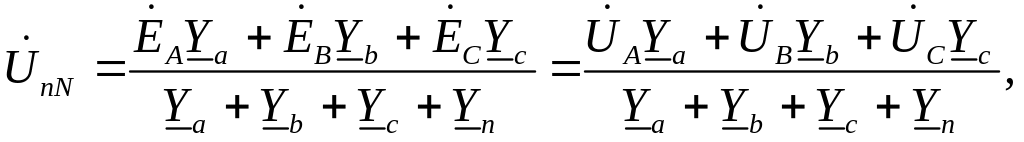(3.7)

где комплексные проводимости фаз и нулевого провода соответственно.

Тогда токи в фазах нагрузки определятся с учетом (3.5)

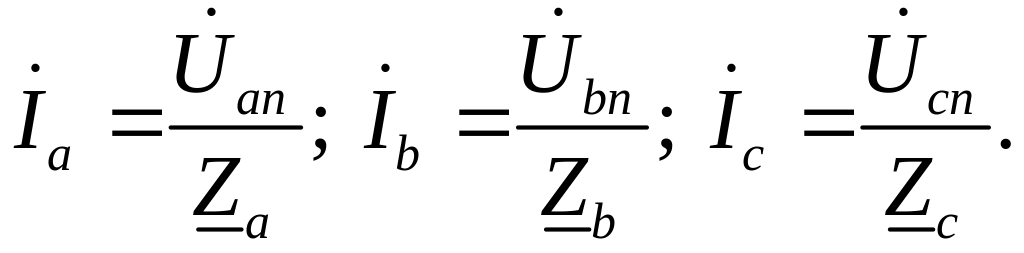(3.8)

Ток в нулевом проводе

В предельном случае, когда сопротивление нулевого провода равно нулю, т.е. Y_n=∞, напряжение между нулевыми точками также равно нулю. Тогда фазные напряжения на нагрузке равны соответствующим фазным напряжениям источника, и расчет можно вести по формулам (3.6).

Если нулевой провод отсутствует, то в выражении (3.7) следует положить

а расчет фазных токов вести по выражениям (3.8).

2.Схема при соединении нагрузки треугольником

При соединении нагрузки треугольником не принципиально, по какой схеме соединены обмотки генератора, т.к. к нагрузке подводятся линейные напряжения, а нулевой провод отсутствует. Поэтому для расчета достаточно рассмотреть схему со стороны нагрузки, представленную на рис. 3.5.

Токи в фазах определяются по закону Ома:

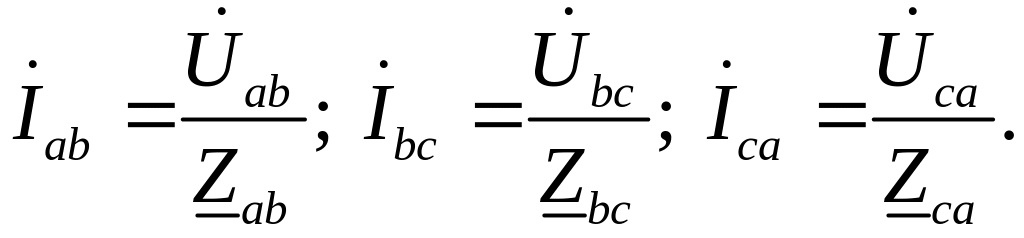(3.9)

Линейные токи определяются по формулам (3.3).