1.8. Определение множества состояний по внутренней структуре

Промежуточные и выходные переменные в дальнейшем изложении будут называться зависимыми переменными. В большинстве случаев, представляющих практический интерес, имеется достаточная информация о внутренней структуре системы для определения всех переменных, которые характеризуют поведение системы. Более того, можно определить значение любой зависимой переменной в любой тактовый момент, если известны значения входных переменных в этот момент и значения зависимых переменных в предыдущий тактовый момент. В таких случаях, как будет показано ниже, существует методика определения множества состояний системы.

Пусть заданы входные переменные системы x⁽¹⁾, x⁽²⁾, ..., x^(u), выходные переменные системы z^(l), z⁽²⁾, ..., z^(w) и зависимые переменные системы у⁽¹⁾, у⁽²⁾, ..., у^(r) (множества зависимых переменных включает в себя все выходные переменные). Предположим, что для каждой зависимой переменной y^(k) структура системы дает следующее соотношение:

y^(k)_ν= g_k(x⁽¹⁾_ν, x⁽²⁾_{ν, ...,} x^(u)_ν, y⁽¹⁾_ν-1, y⁽²⁾_ν-1, ..., y^(r)_ν-1). (1.9)

На основании § 1.4 входные переменные можно представить одной переменной х с алфавитом

, (1.10)

где X⁽ⁱ⁾, i=1,2,..., u, является алфавитом x⁽ⁱ⁾; выходные переменные можно представить одной переменной z с алфавитом

, (1.11)

где Z^(j), j = l, 2, ...,w, является алфавитом z^(j). Аналогично зависимые переменные можно представить одной переменной у с алфавитом

, (1.12)

где Y^(k), k = 1, 2, ..., r, является алфавитом y^(k). Тогда выражение (1.9) можно записать так:

y_ν = g_y(x_ν, y_ν-1). (1.13)

Так как каждая выходная переменная является зависимой переменной, мы также имеем:

z_ν = g_z(x_ν, y_ν-1). (1.14)

Для перехода от приведенных выше формул к стандартным характеристическим функциям f_z и f_s, конечного автомата определим переменную s следующим образом:

s_ν = y_ν-1. (1.15)

Тогда алфавит s, обозначаемый через S, определяется формулой

S=Y. (1.16)

Выражения (1.13) и (1.14) можно теперь записать так:

y_ν = f_s(x_ν, s_ν). (1.17)

z_ν = f_s(x_ν, s_ν). (1.18)

Из (1.15) и (1.17) получаем:

s_ν+1 = f_z(x_ν,s_ν). (1.19)

Как теперь видно, уравнения (1.18) и (1.19) выражают искомые характеристические функции. Следовательно, S составляет требуемое для описания заданной системы множество состояний.

Для примера рассмотрим схему, показанную на рис. 1.4. На вход υ_вх от источника поступают импульсы со значением О

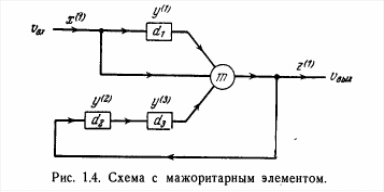
и 1 со скоростью один импульс в каждые Т секунд. Тактовые моменты выбраны совпадающими с моментами появления импульсов. Элементы d₁, d₂, d₃ — задержки, которые запоминают поступающие на них импульсы на Т секунд и затем передают их на следующий за ними элемент. Элемент m представляет собой «мажоритарный орган», который выдает импульс 0 или 1 в зависимости от значения (0 или 1

соответственно) большинства поступающих на его входы импульсов. Нас интересует значение импульса на выходе υ_вых. Значение импульса на входе схемы υ_вх в момент t_v можно принять в качестве входной переменной x⁽¹⁾ , а значение импульса на выходе v_вых в момент t_v — в качестве выходной переменной z⁽¹⁾. Значения импульсов, запомненные элементами d₁, d₂ и d₃, в момент t_v можно принять в качестве зависимых переменных у⁽¹⁾, у⁽²⁾ и у⁽³⁾ соответственно. Тогда имеем:

Х={0, 1},

Z={0, 1},

S= {(000), (001), (010), (011), (100), (101), (110), (111)}.

Из схемы видно, что у⁽¹⁾_v = х⁽¹⁾_v , у⁽²⁾_v = z⁽¹⁾_v и y⁽³⁾_v = у⁽²⁾_v-1; значение z⁽¹⁾_v равно значению большинства переменных у⁽¹⁾_v-1, х⁽¹⁾_v и у⁽³⁾_v-1. Используя эти соотношения, можно определить значения функций:

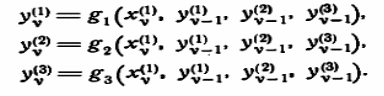
Результаты вычислений представлены в таблице 1.1. Из определения s следует, что каждая строка части таблицы, состоящей из столбцов у⁽¹⁾_v-1, у⁽²⁾_v-1 и у⁽³⁾_v-1, представляет собой состояние s_v, а каждая строка части таблицы, состоящей из

столбцов у⁽¹⁾_v, у⁽²⁾_v и у⁽³⁾_v —состояние s_v+1. Учитывая, что х⁽¹⁾_v= х_v и y⁽¹⁾_v= z_v, можно сделать вывод, что таблица 1.1 полностью описывает характеристические функции рассматриваемой схемы. Например, из таблицы легко определить (см. четвертую строку), что при состоянии в настоящий момент (001) и входном символе в этот же момент 1 выход в настоящий момент будет 1, а следующее состояние (11О).