2.8. Матрица переходов13

Матрицы переходов являются математической копией графов переходов; они дают возможность формализовать ряд операций, которые на графе переходов могут быть выполнены визуально. Матрицы переходов поэтому имеют преимущества в тех случаях, когда эти операции не могут быть выполнены человеком-исследователем и, следовательно, не могут быть выполнены визуально или когда граф переходов настолько сложен, что использование визуальной методики бесполезно.

Для автомата М, имеющего n состояний, матрица переходов состоит из n. строк и n столбцов и обозначается [М]. Пусть {σ₁, σ₂, .:., σ_n}—множество состояний автомата М и пусть b_ij обозначает дугу графа переходов автомата М, направленную от σ_i к σ_j. Элемент (i, j) (т. е. содержимое клетки, расположенной на пересечении i-й строки и j-го столбца матрицы [М] обозначается е_ij и определяется так:

Для ясности обычно обозначение k-го состояния σ_k приписывают k-й строке и k-му столбцу и называют их «строка σ_k» и «столбец σ_k» соответственно. Выражение (2.12) изображает матрицу переходов автомата А1, заданного в виде графа на рис. 2.2.

Если р — мощность входного алфавита автомата М, то каждая строка в [М] должна содержать точно р пар вход-выход, причем каждая пара имеет входной символ, отличный от входного символа любой другой пары. Дуги, заходящие в состояние σ_k, представляются недиагональными элементами¹⁴ столбца σ_k; дуги, исходящие из состояния σ_k, представляются недиагональными элементами строки σ_k ; петля состояния σ_k представляется диагональным элементом в строке σ_k или

столбце σ_k. Следовательно, если σ_k — переходящее состояние, то все недиагональные элементы в столбце σ_k (но не в строке σ_k) равны нулю; если σ_k —тупиковое состояние, то все недиагональные элементы в строке σ_k (но не в столбце σ_k) равны нулю; если σ_k —изолированное состояние, то все недиагональные элементы в строке σ_k и столбце σ_k равны нулю.

Если S_i = {σi₁, σi₂, ..., σi_r}, то определенное в § 2.6 множество G₁ (S_i) представляет собой объединение S_i и обозначений столбцов, в которых элементы, принадлежащие строкам σi₁, σi₂, ..., σi_r, не равны нулю. Определенное в § 2.7 множество H_I(S_i) представляет собой объединение S_i обозначений столбцов, в которых элементы, принадлежащие строкам σi₁, σi₂, ..., σi_r, не равны нулю, и обозначений строк, в которых элементы, принадлежащие столбцам σi₁, σi₂, ..., σi_r, не равны нулю. Например, из матрицы [Al] ясно видно, что для автомата A1 G₁(l, 2) = {1, 2, 3} и Н₁(4, 5)={1, 3, 4, 5}. Таким образом, ясно, что матрица переходов является удобным инструментом для выполнения алгоритмов 2.1, 2.2 и 2.3.

Для того чтобы определить, составляет ли множество S(σi₁, σi₂, ..., σi_r) преходящий, тупиковый или изолированный подавтомат автомата М, надо строки и столбцы матрицы [М] переставить так, чтобы строки и столбцы σi₁, σi₂, ..., σi_r заняли соседние положения, начиная с первой строки и первого столбца соответственно. Как показано в (2.13), эта перестановка делит матрицу [М] на четыре подматрицы [М₁₁], [М₁₂], [M₂₁], [М₂₂], причем строками и столбцами [М₁₁] являются строки и столбцы σi₁, σi₂, ..., σi_r

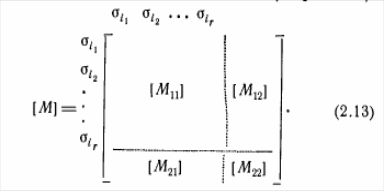
Обозначая матрицу, все элементы которой равны нулю, через [0], можно сделать вывод, что S_i составляет преходящий подавтомат, если [M₂₁] = [0], а [М₁₂] ≠ 0, тупиковый подавтомат, если [М₁₂] = [0], а [M₂₁] ≠ 0, и изолированный подавтомат, если [М₁₂] = [М₂₁] = [0]. В (2.14) представлена матрица переходов автомата A3, изображенного на рис. 2.5, в которой строки и столбцы переставлены так, чтобы выделить тупиковый подавтомат {1, 4, 7}, преходящий подавтомат {2, 5, 8} и изолированный подавтомат {3, 6, 9}.

Если S_i составляет тупиковый или изолированный подавтомат, то [M₁₂] = [0] и, следовательно, каждая строка в [М₁₁] содержит все р пар вход-выход, где р — мощность входного алфавита. Удалив [M₁₂], [M₂₁] и [М₂₂] из [М], получим матрицу [М₁₁] размером r r, которую можно трактовать как матрицу, представляющую независимый автомат М₁₁ с r состояниями, имеющий тот же входной алфавит, что и М. Отсюда следует то же заключение, которое было получено в § 2.6: если автомат находится в состоянии, принадлежащем тупиковому или изолированному подавтомату, то все состояния, которые не принадлежат этому подавтомату, и все дуги, исходящие из этих состояний, могут быть исключены.