Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Изучение колебаний связанных маятников

Методические указания к лабораторной работе

по курсу общей физики

Составитель: С. А. Чудинова, к. ф.-м. н., доцент кафедры общей физики

Рецензент: А. И. Назаров, д. п. н., к. ф.-м. н., профессор кафедры общей физики

Петрозаводск

2009

Изучение колебаний связанных маятников

Цель работы:

Экспериментальным путем изучить особенности колебаний связанных механических систем с двумя степенями свободы.

Задачи:

1. Определить коэффициент упругости пружины по ее растяжению.

2. Определить собственные частоты колебаний несвязанных маятников и рассчитать их момент инерции.

3. Определить собственные частоты колебаний системы двух маятников, связанных пружиной, для следующих случаев:

• колебания "в фазе";

• колебания "в противофазе".

4. Определить парциальные частоты колебаний при некотором произвольном режиме движения системы и исследовать их зависимость от длины сцепления.

5. Определить коэффициент связи маятников.

Теоретическое введение Сложение гармонических колебаний

Колебания являются одной из форм движения механической системы и характеризуются его повторяемостью через некоторый промежуток времени Т, называемый периодом колебаний. При небольших отклонениях от положения равновесия колебания бывают гармоническими, т. е. описываются законом:

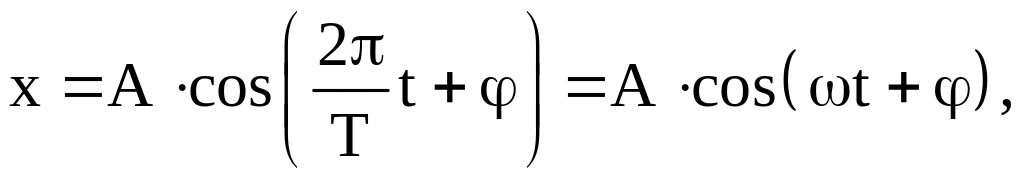(1)

где х – смещение точки от положения равновесия в некоторый момент времени t; – фаза колебания (аргумент функции косинус); φ – начальная фаза колебания; А – амплитуда колебания (А = х_max); ω = 2π/Т – циклическая частота колебания.

Г рафик гармонического колебания изображен на рис. 1.

Рис. 1. График гармонического колебания

Дважды продифференцировав уравнение (1), получим связь между ускорением и смещением:

а = –ω²х. (2)

Если материальная точка участвует одновременно в нескольких колебаниях, то результирующее движение может быть очень сложным и зависит от направлений исходных колебаний, а также от соотношения их частот, амплитуд и фаз.

К олебание (1) можно наглядно представить с помощью векторной диаграммы (рис. 2). Для этого изобразим в декартовых координатах вектор А, вращающийся вокруг точки О с угловой скоростью, равной циклической частоте колебаний ω. Мгновенное значение смещения х равно проекции вектора амплитуды на ось х:

Рис. 2. Изображение гармонического колебания с помощью векторной диаграммы

Пусть материальная точка участвует в двух колебаниях одинаковой частоты и одинакового направления:

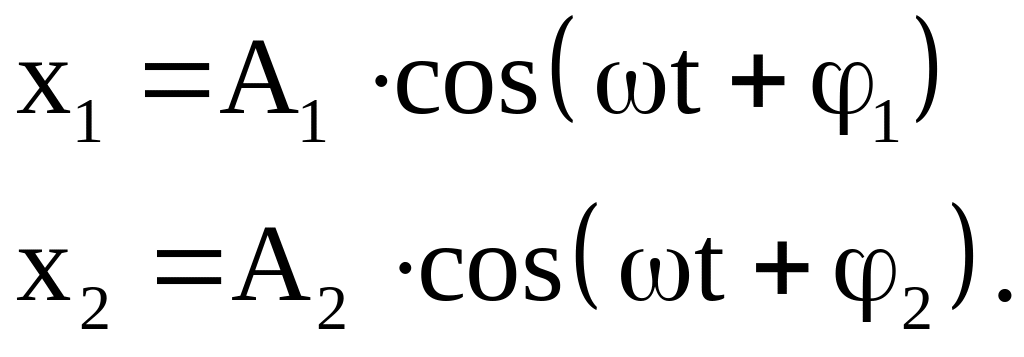
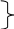
Н а векторной диаграмме (рис. 3) осуществлено сложение этих колебаний и изображен вектор амплитуды А результирующего колебания. Очевидно, вектор А со временем будет вращаться вокруг точки О с той же частотой ω, что и исходные вектора А₁ и А₂. Следовательно, результирующее движение материальной точки, совершающей два синхронных гармонических колебания, будет также гармоническим колебанием, характеризующимся той же частотой.

Рис. 3. Сложение гармонических колебаний

Уравнение суммарного колебания имеет вид Амплитуда результирующего колебания определяется соотношением:

(3)

Формулу (3) легко получить из векторной диаграммы сложения колебаний (рис. 3) по теореме косинусов. Из (3) следует, что амплитуда суммарного колебания зависит от разности фаз Δφ.

Рассмотрим теперь случай, когда колебания х₁ и х₂ происходят с разными частотамий:

Разность фаз этих колебаний со временем будет изменяться:

(4)

Из (3) и (4) следует, что при сложении колебаний с разными частотами амплитуда результирующего колебания А будет со временем изменяться с частотой |ω₁ – ω₂| от максимального значения (А₁ + А₂) до минимального |А₁ – А₂|. Этот процесс периодического изменения амплитуды особенно наглядно проявляется, если частоты исходных колебаний близки, но не равны: Δω = |ω₁ – ω₂| << ω₁ ≈ ω₂.

Н а рис. 4 представлен график колебания х(t), являющегося суммой двух колебаний х₁ и х₂ с близкими частотами. Периодическое изменение амплитуды с частотой |ω₁ – ω₂| называется биением.

Рис. 4. График биения

Частотой биений называется величина

ω_б = |ω₁ – ω₂|, (5)

а периодом биений

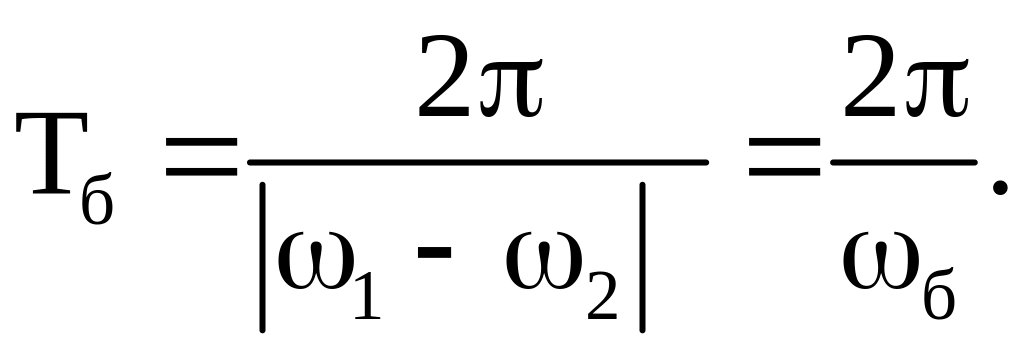(6)

Период биений Т_б и период колебаний Т_кол показаны на рис. 4.