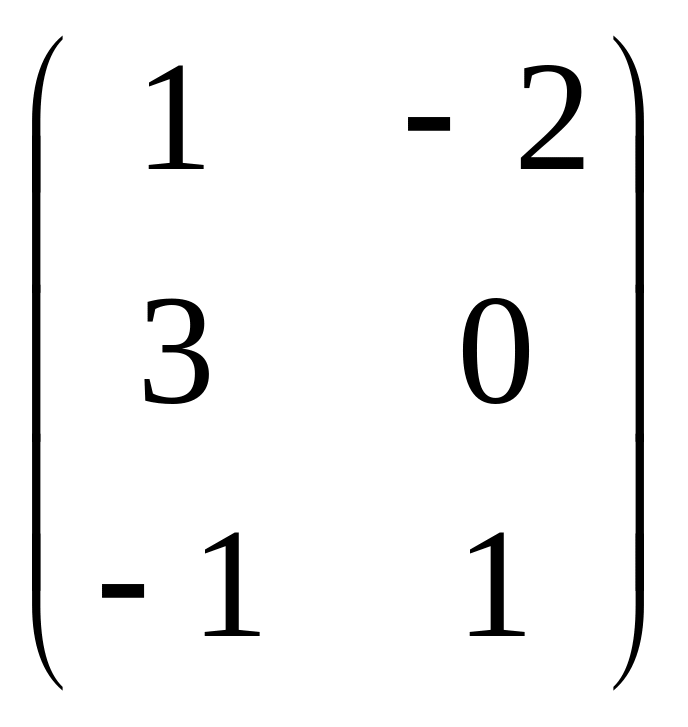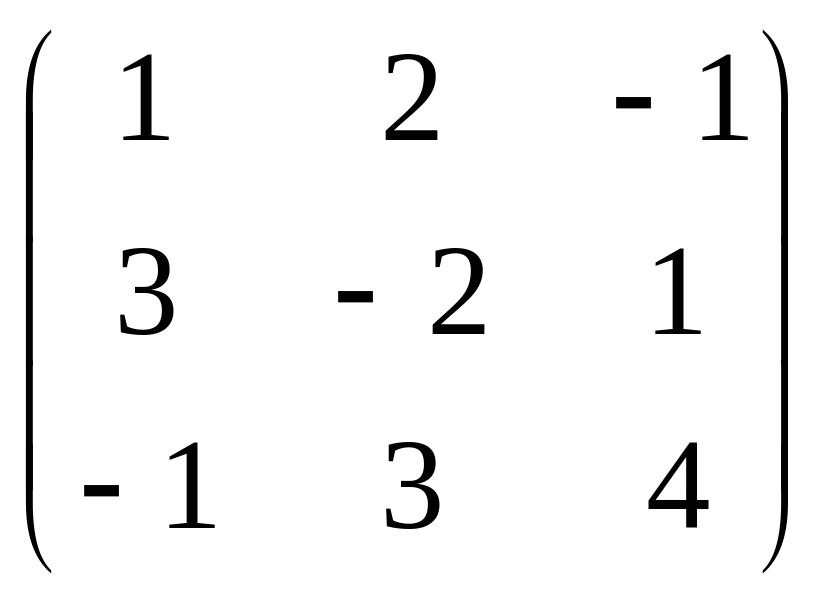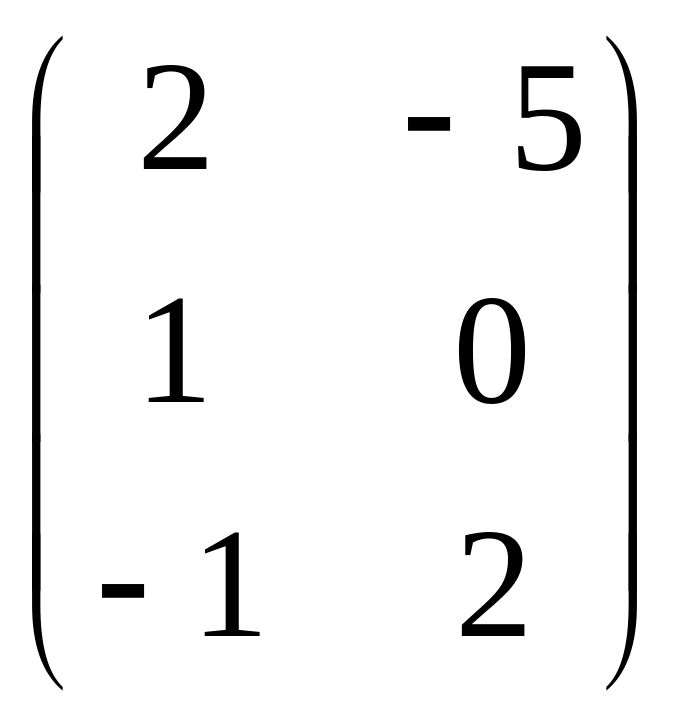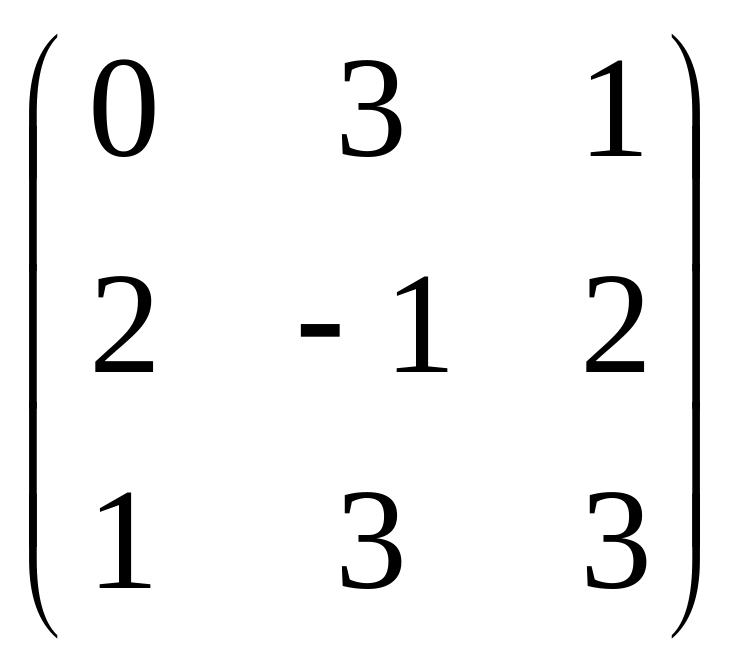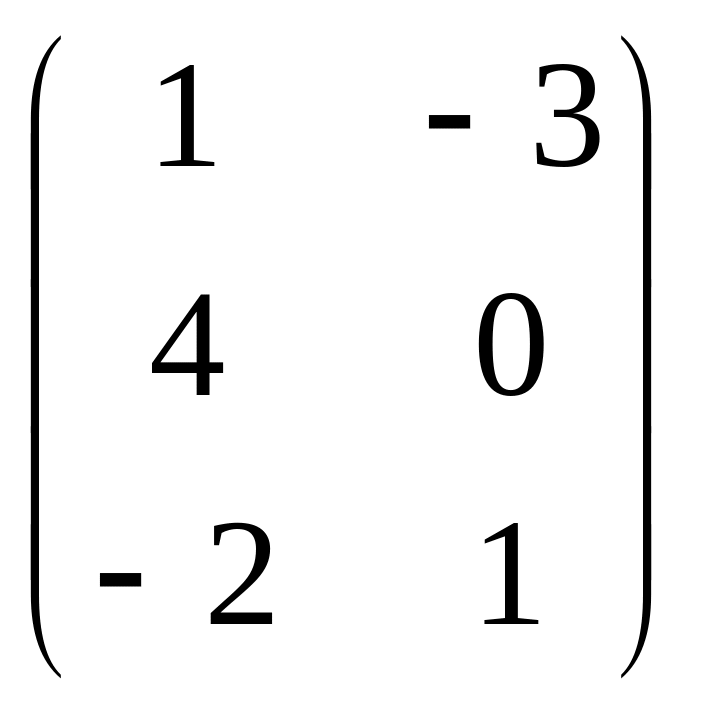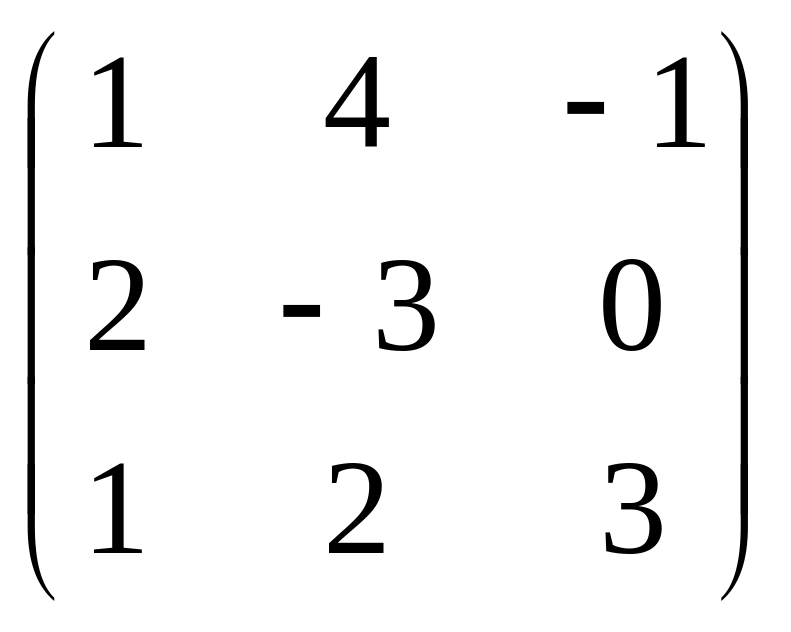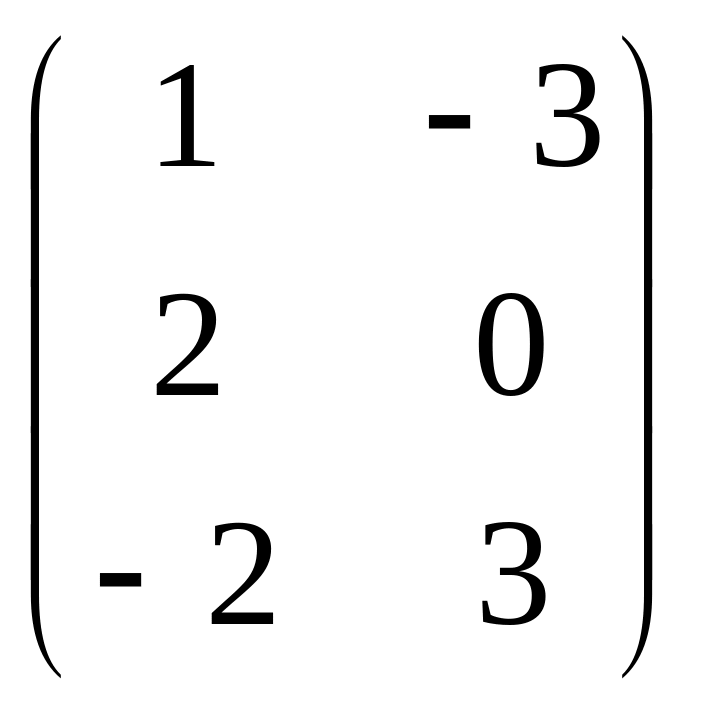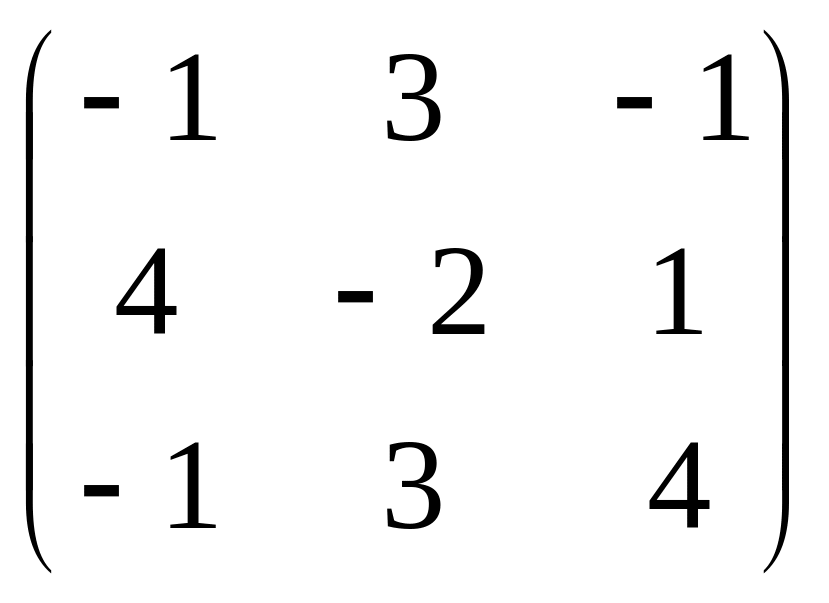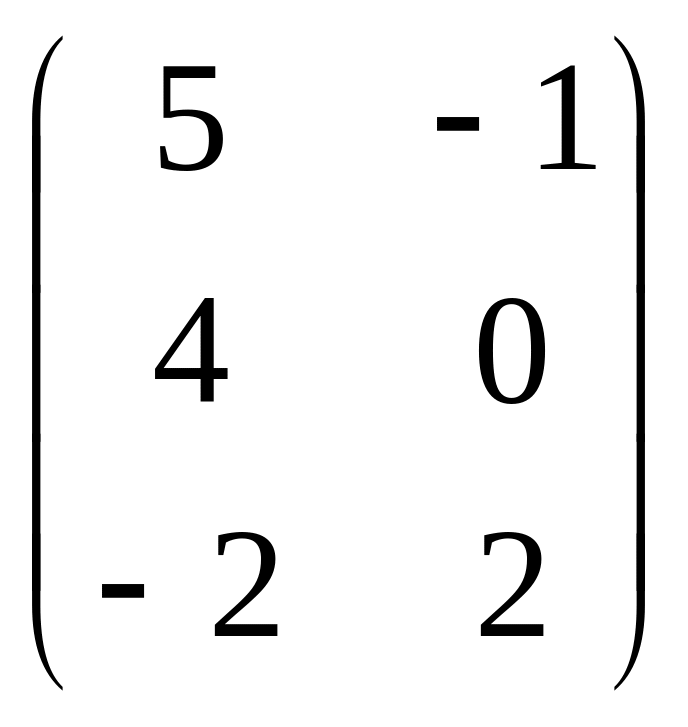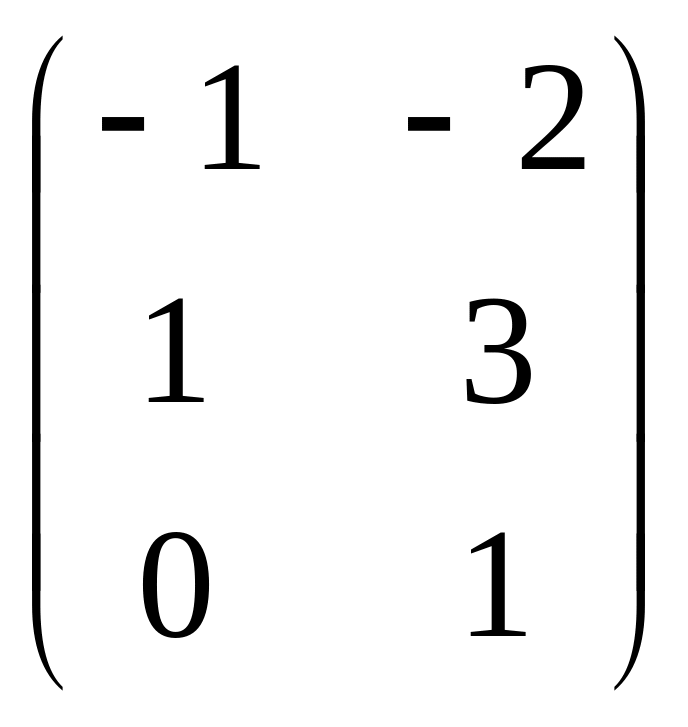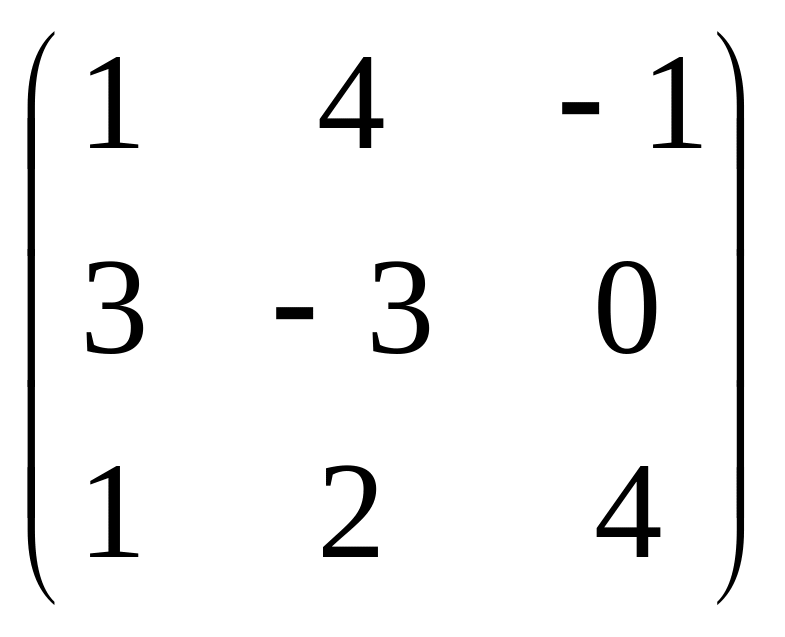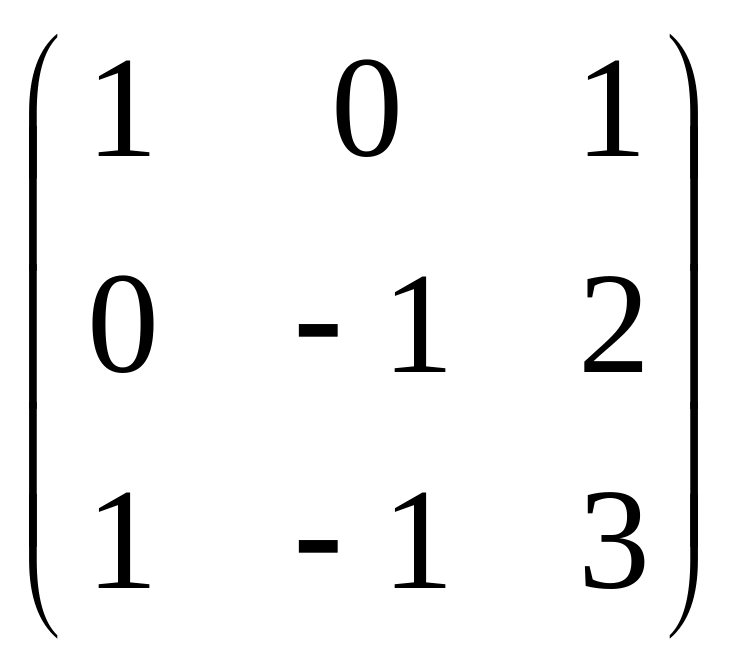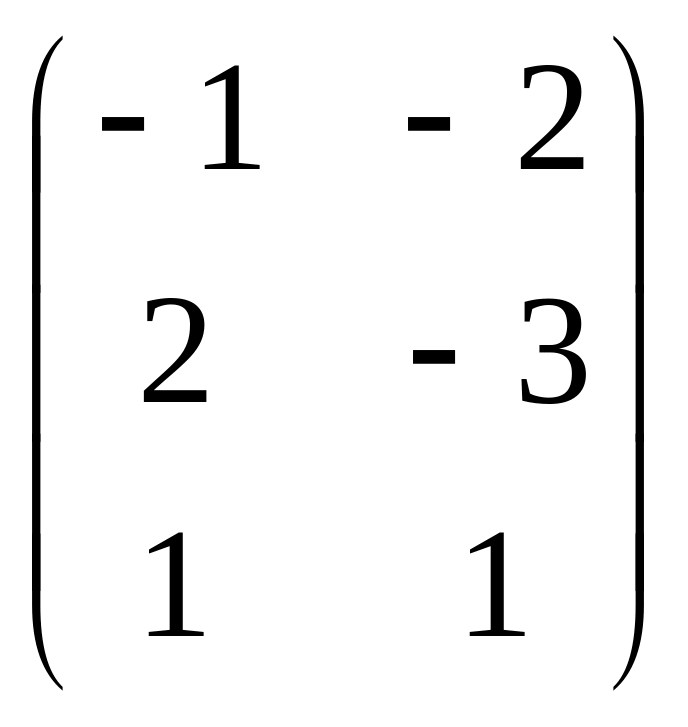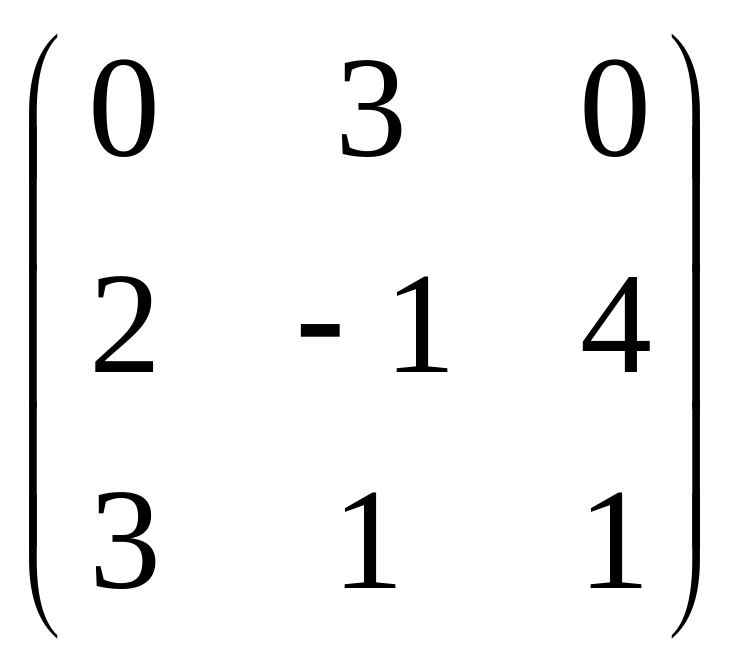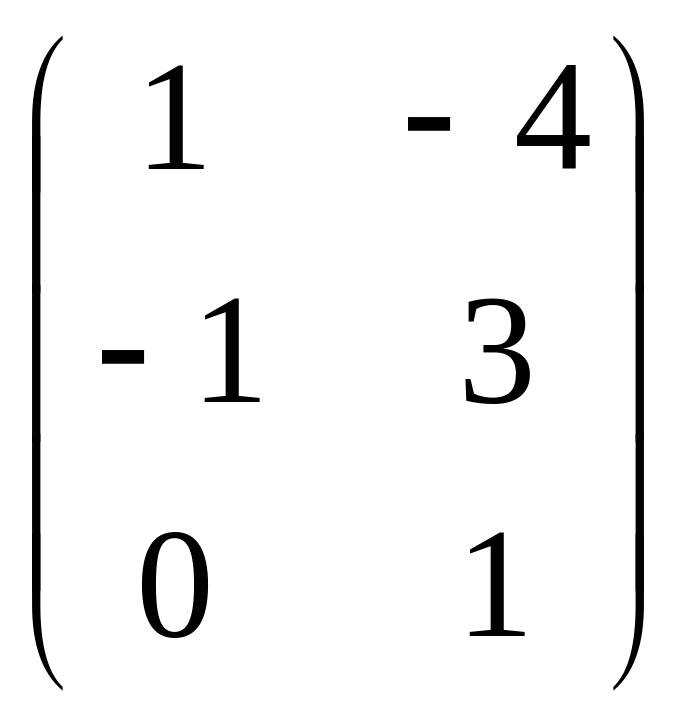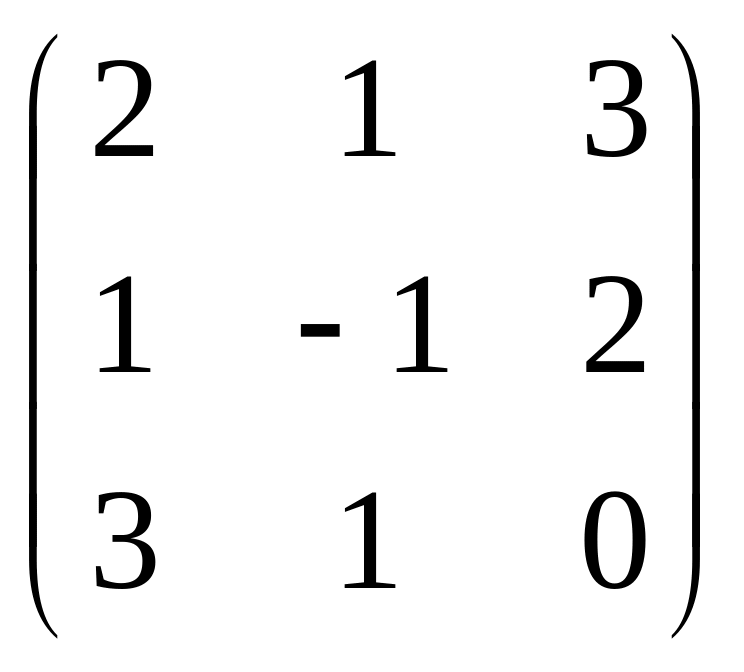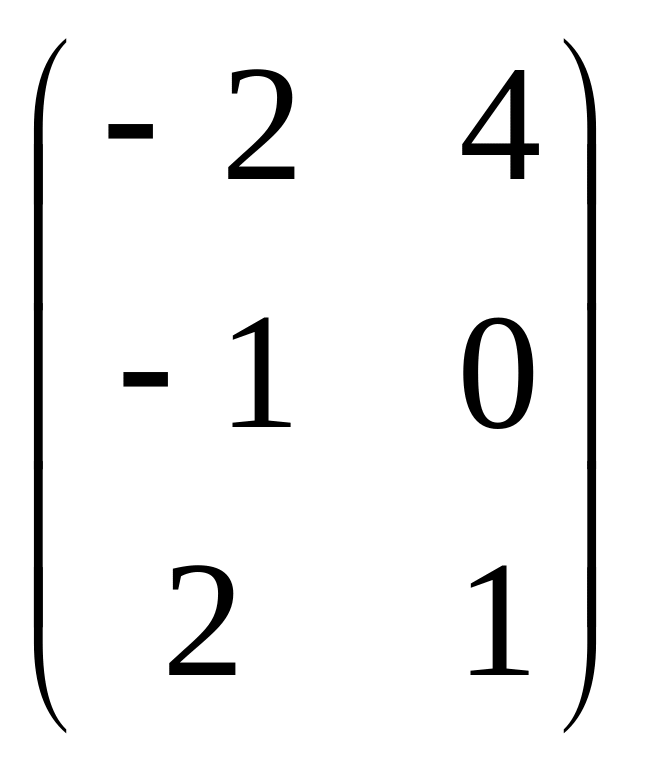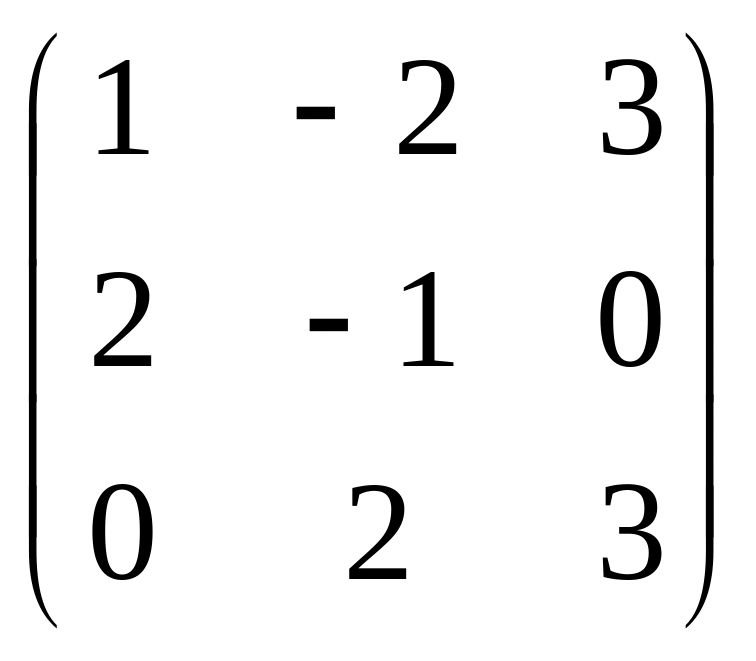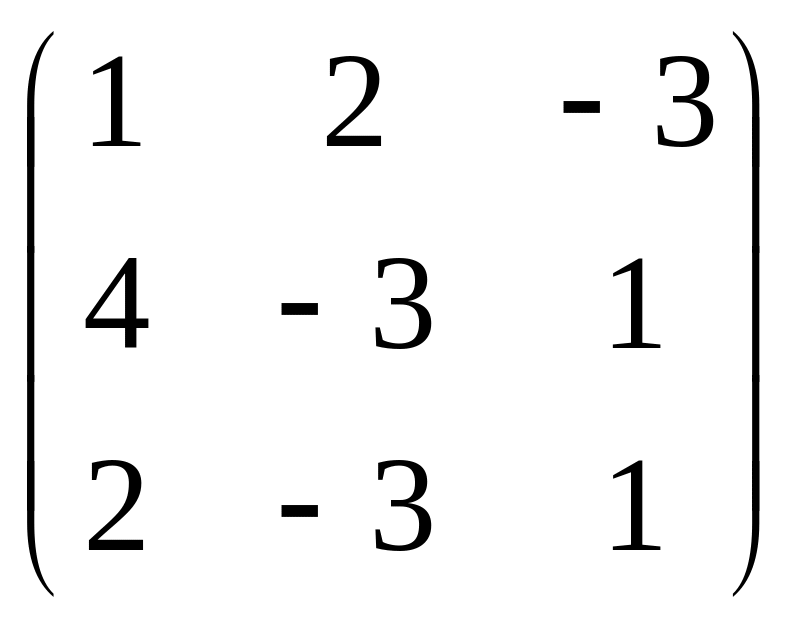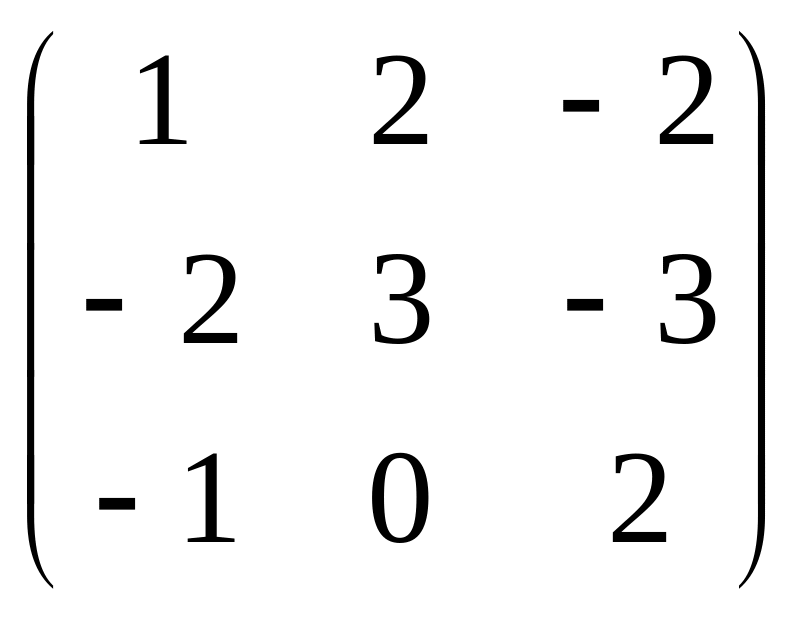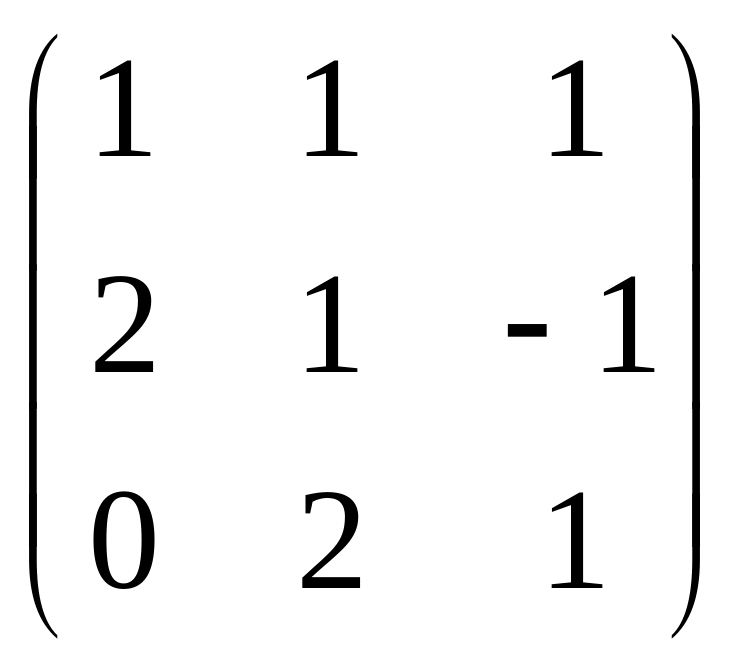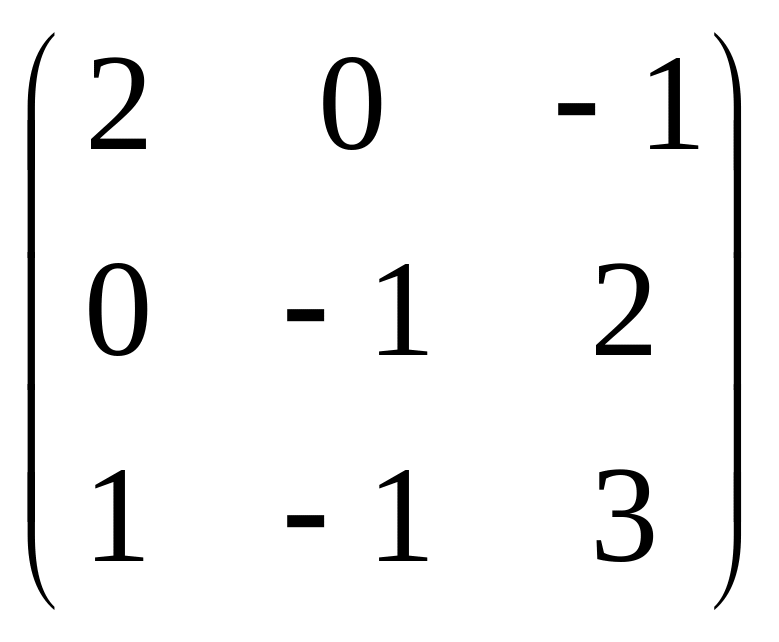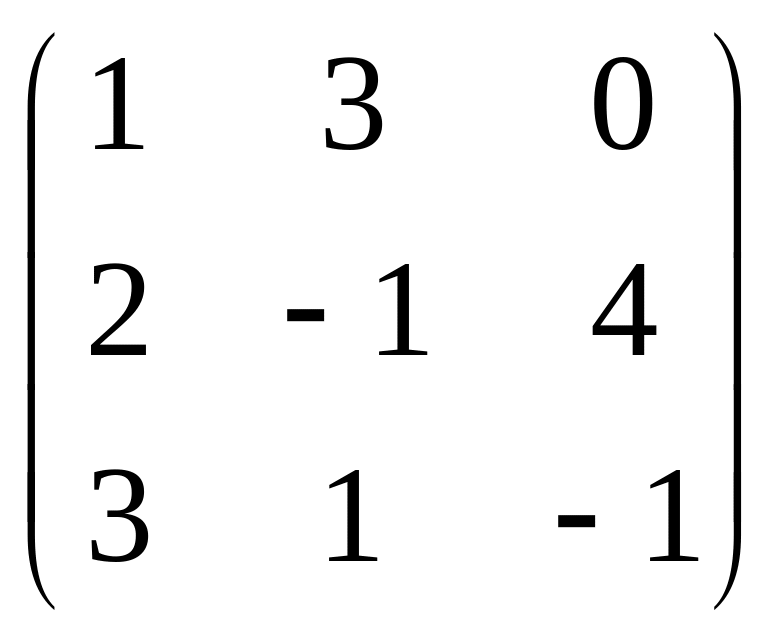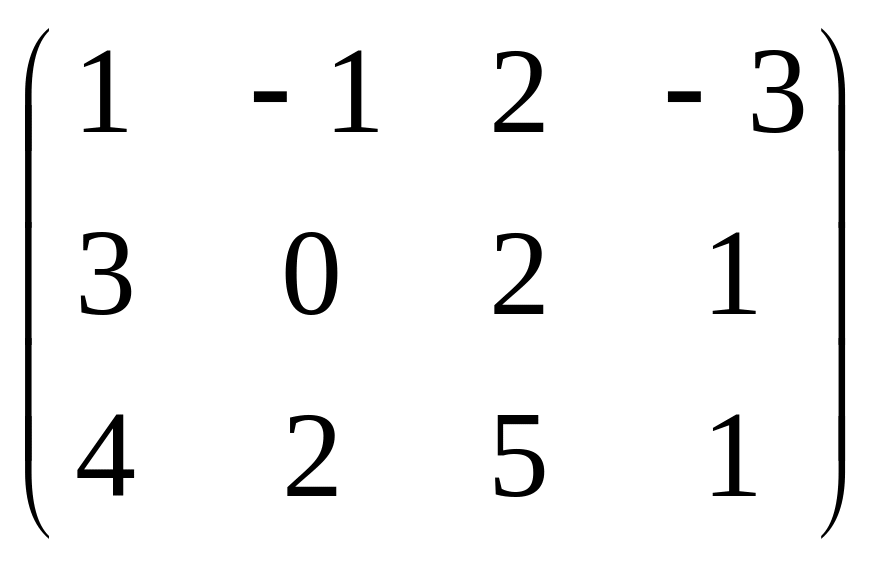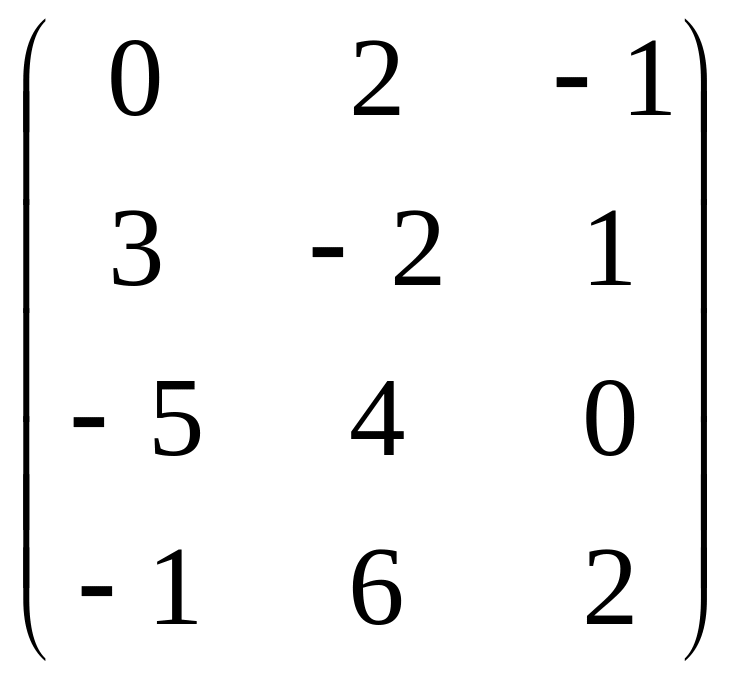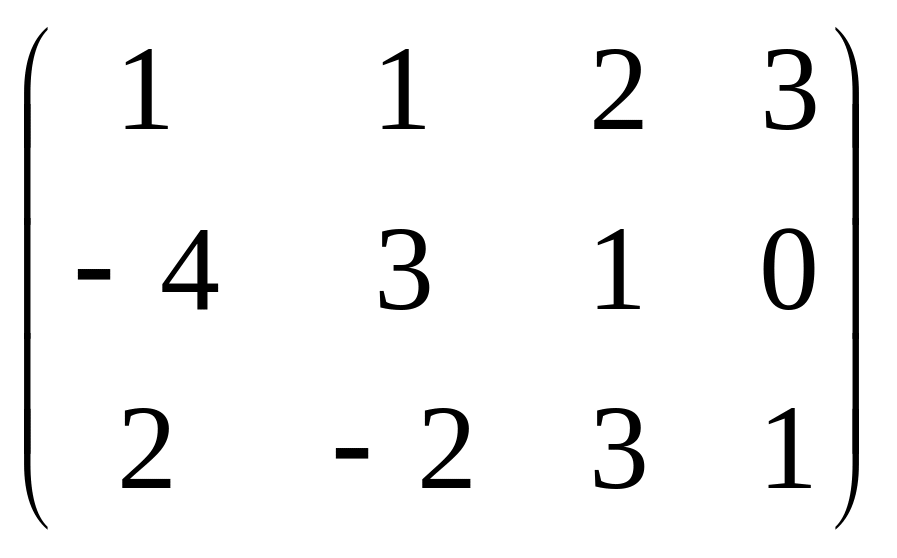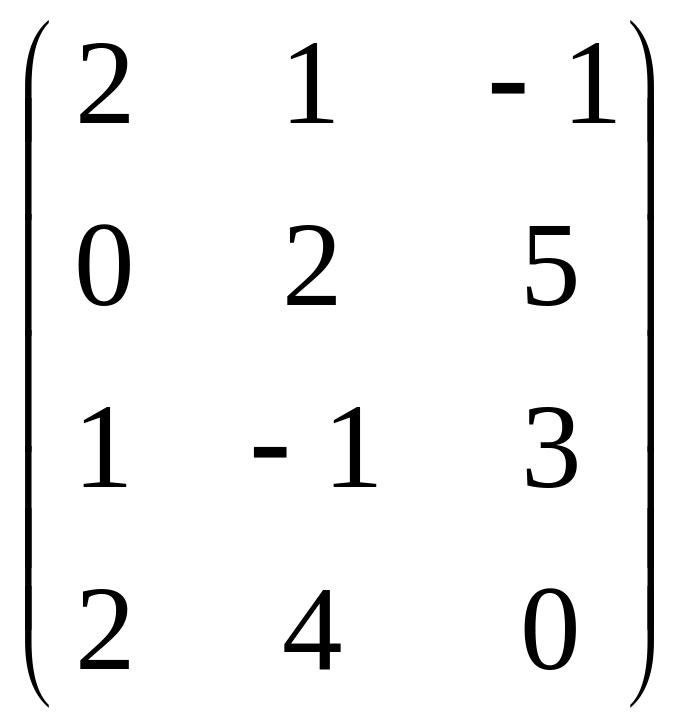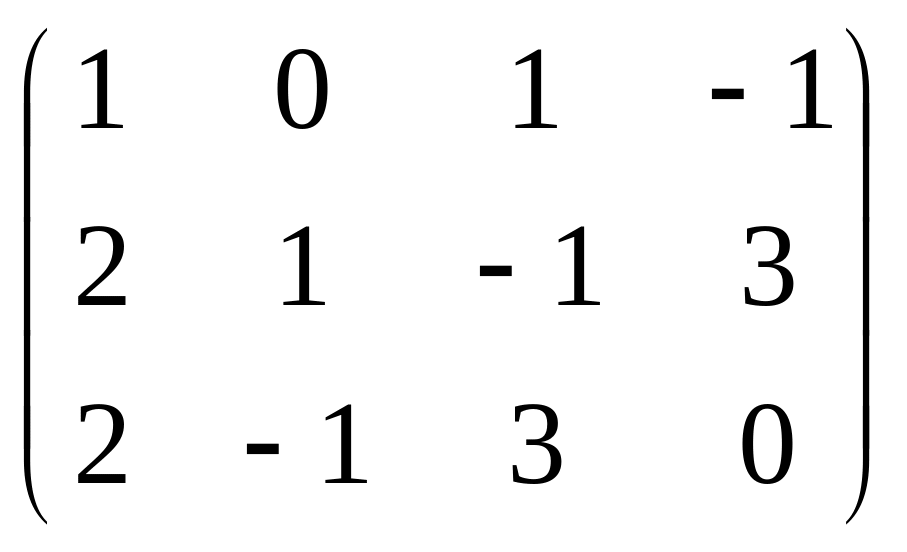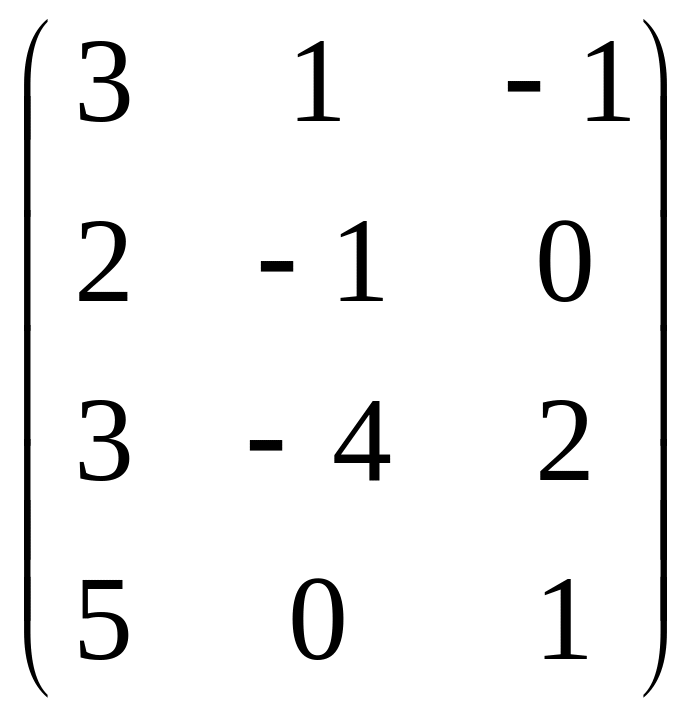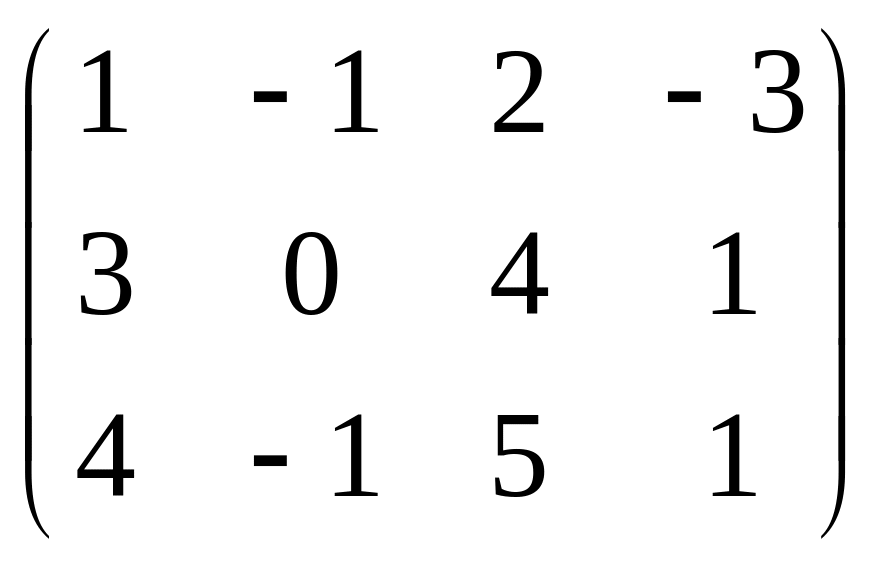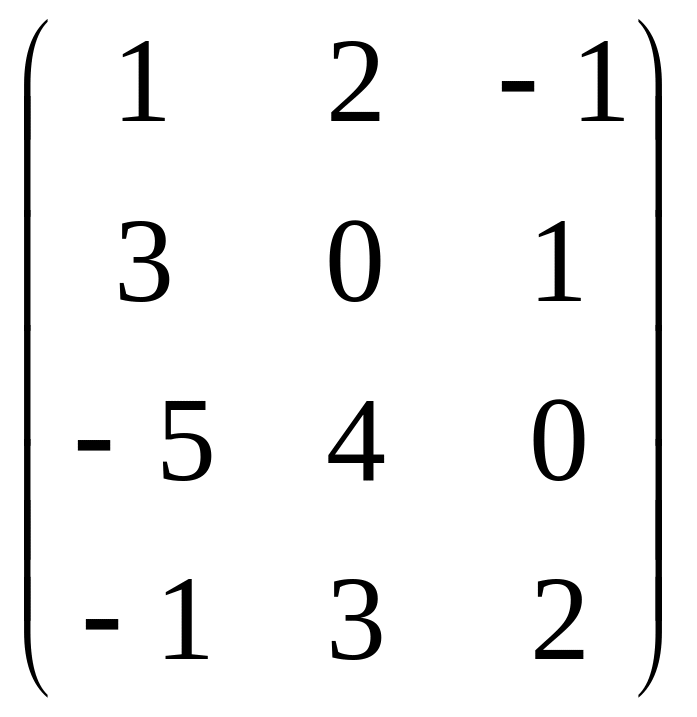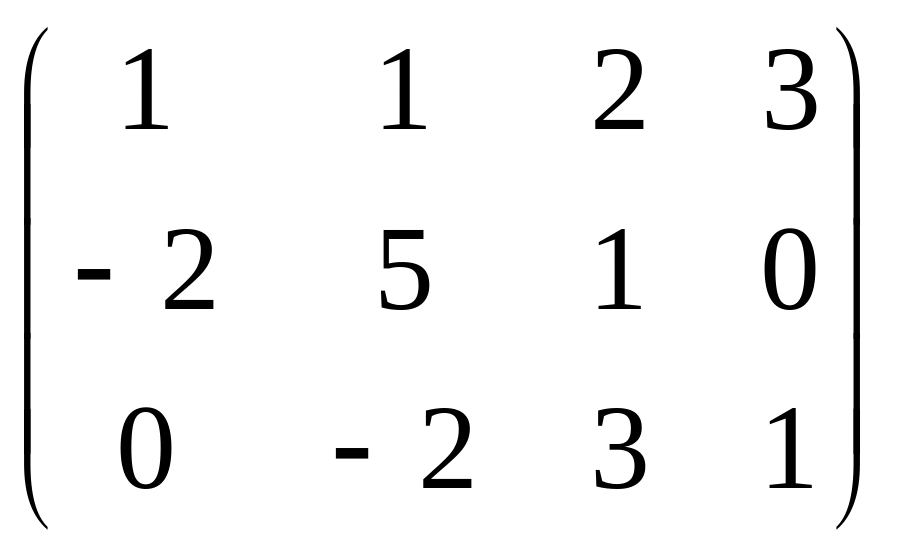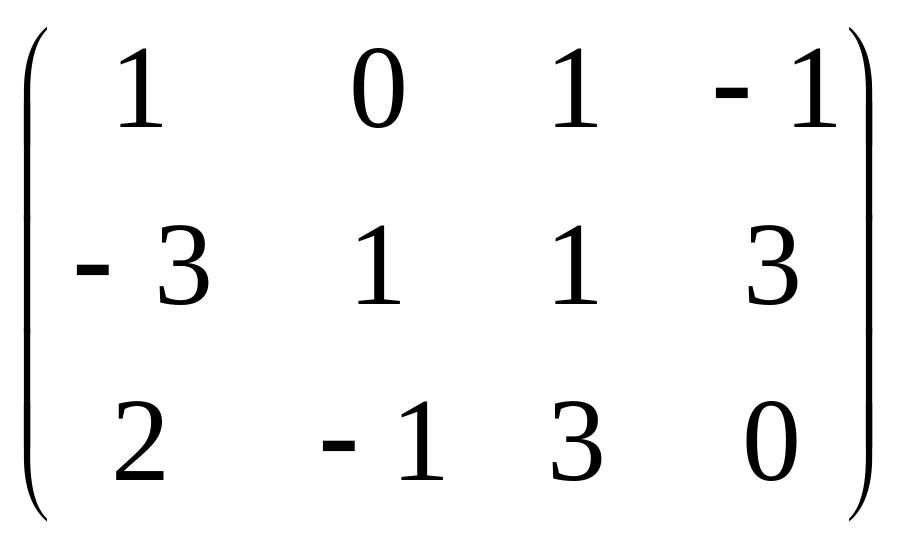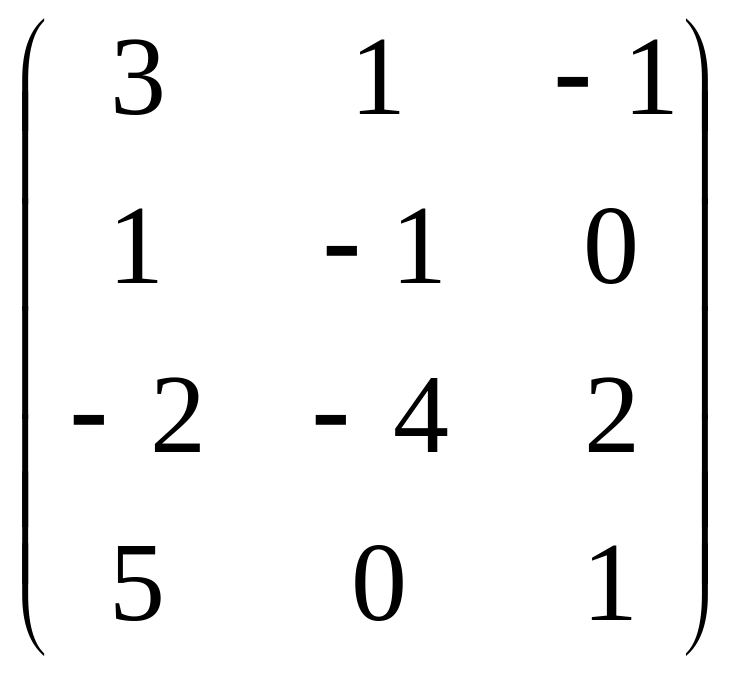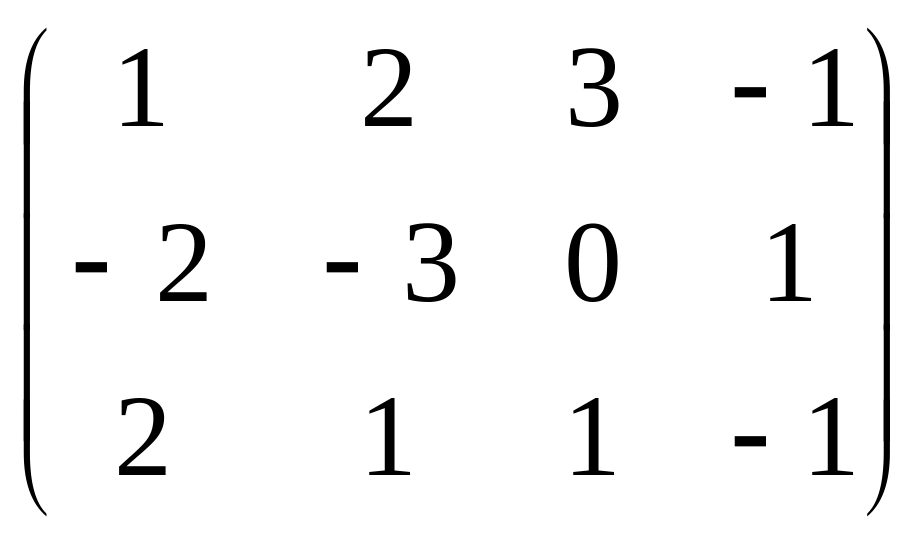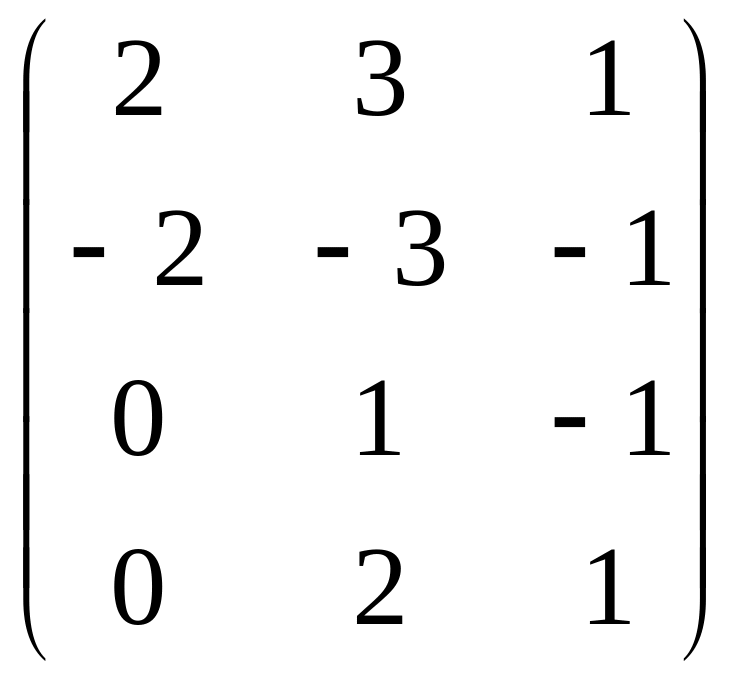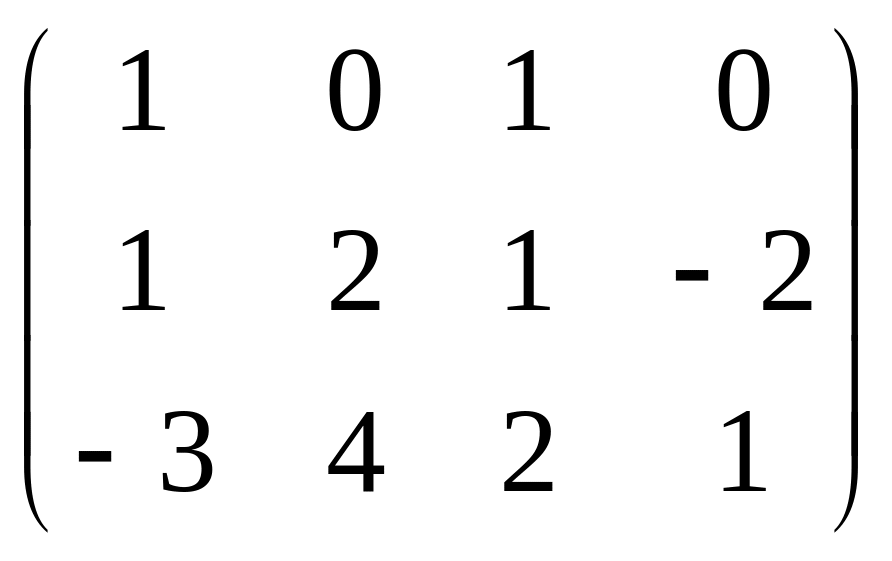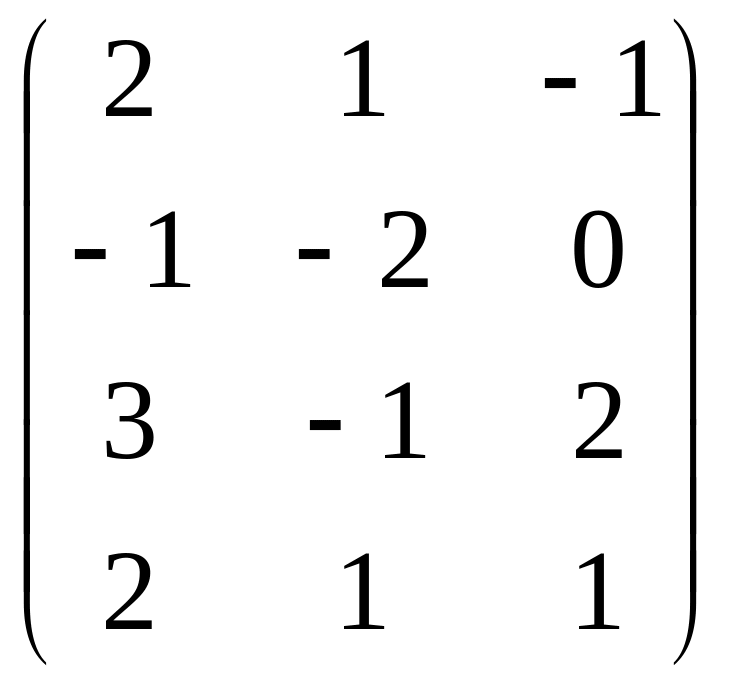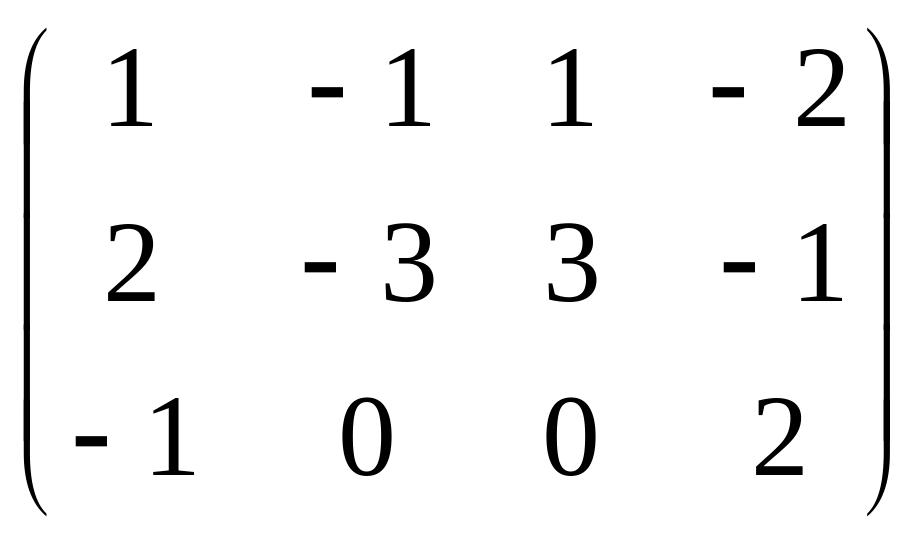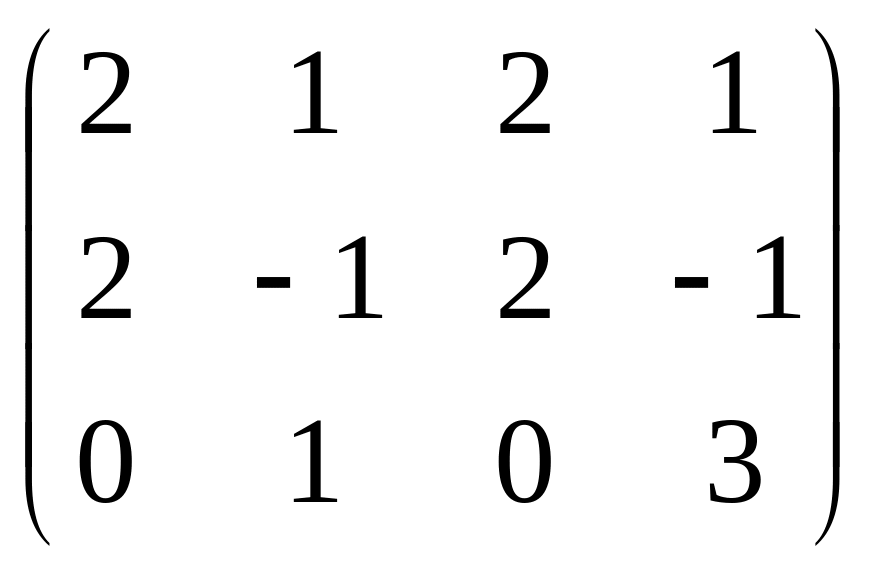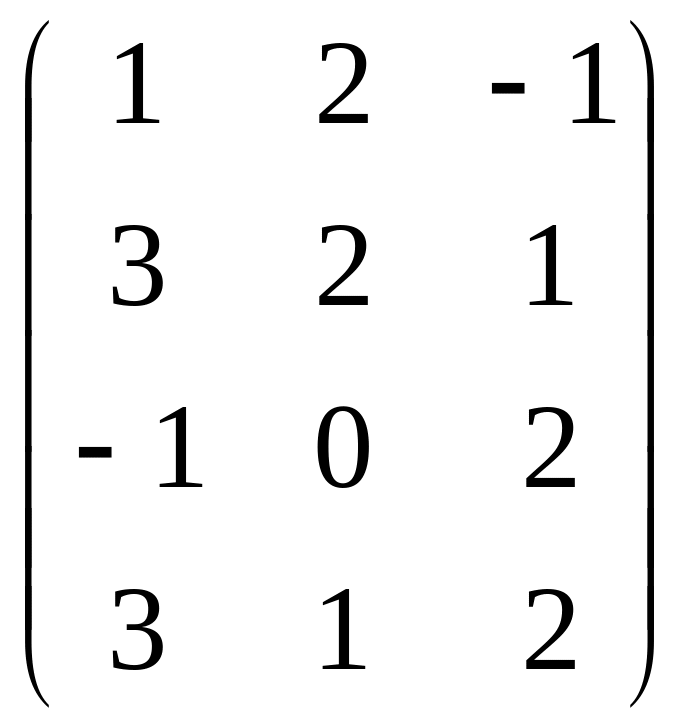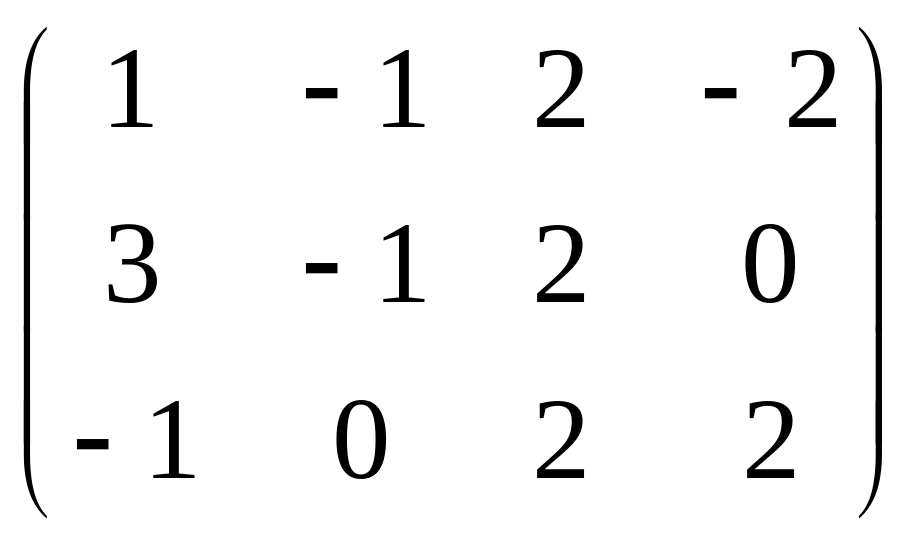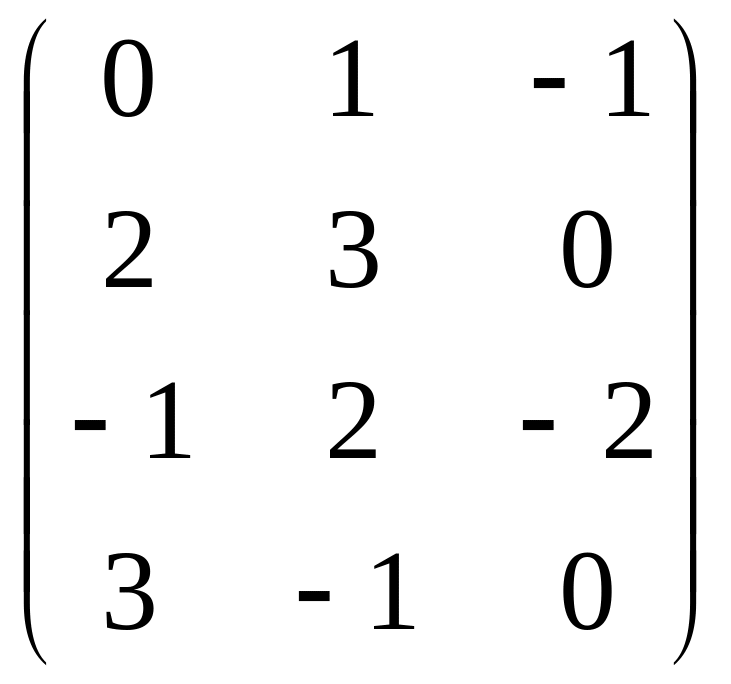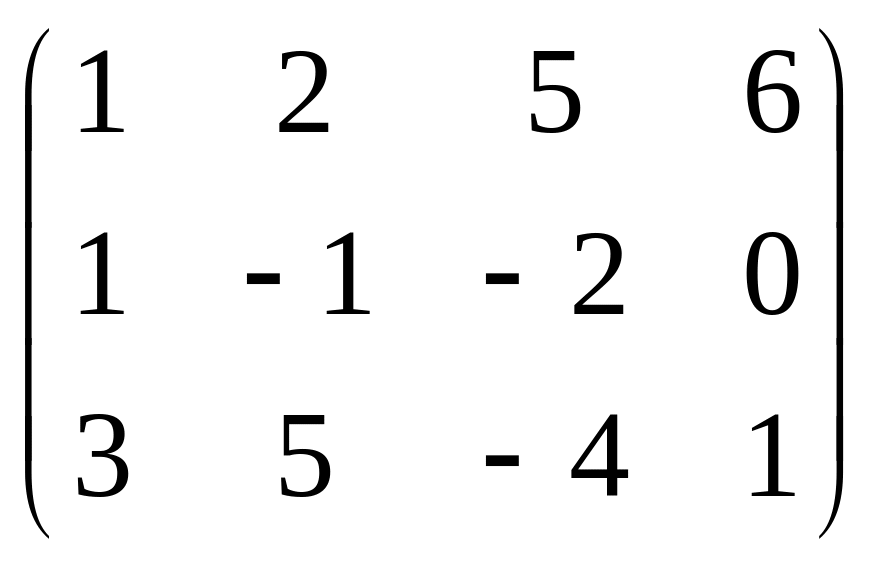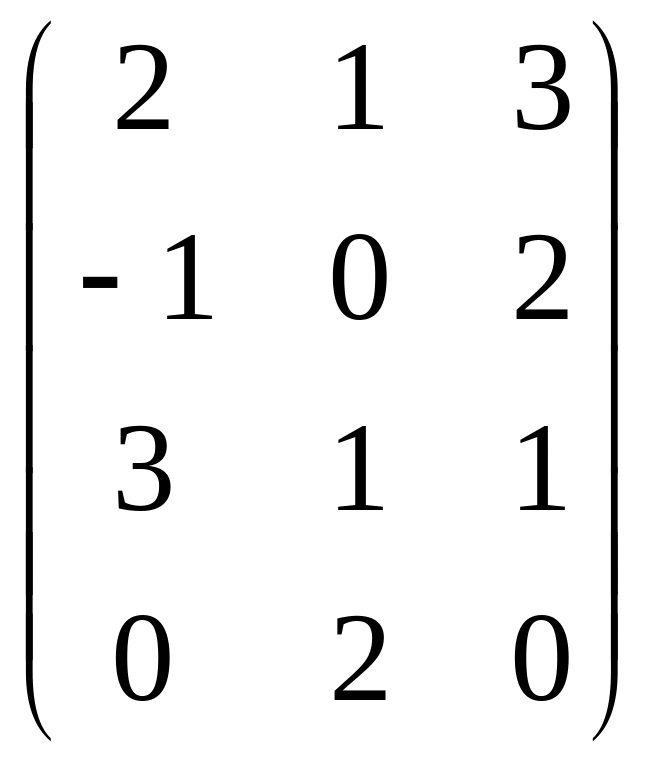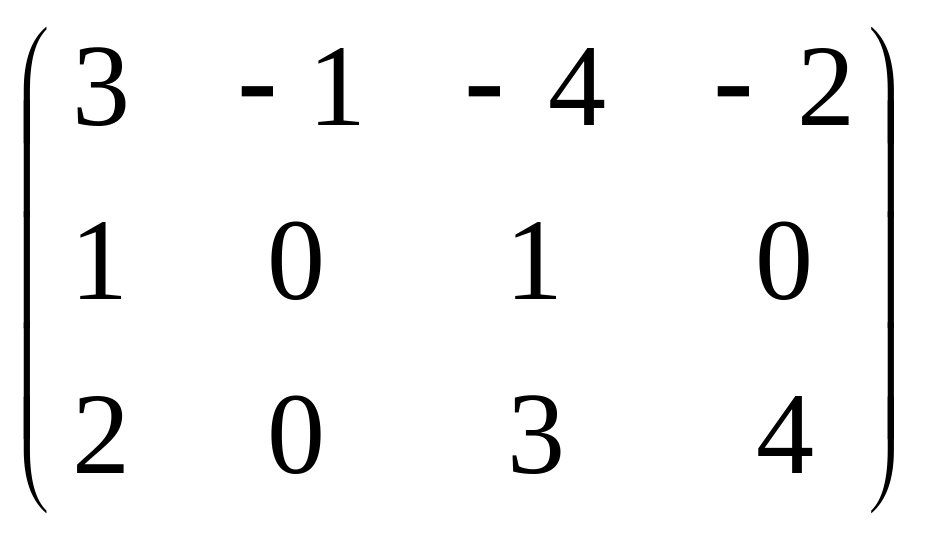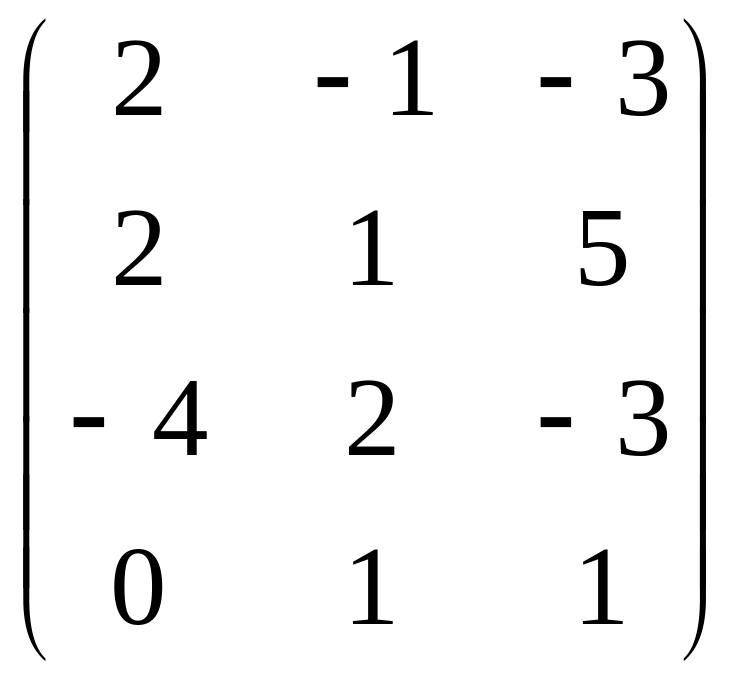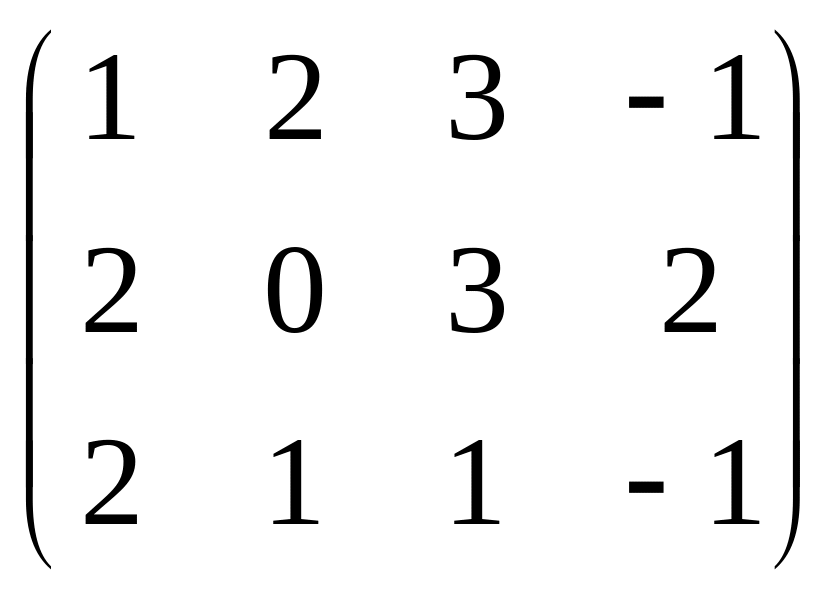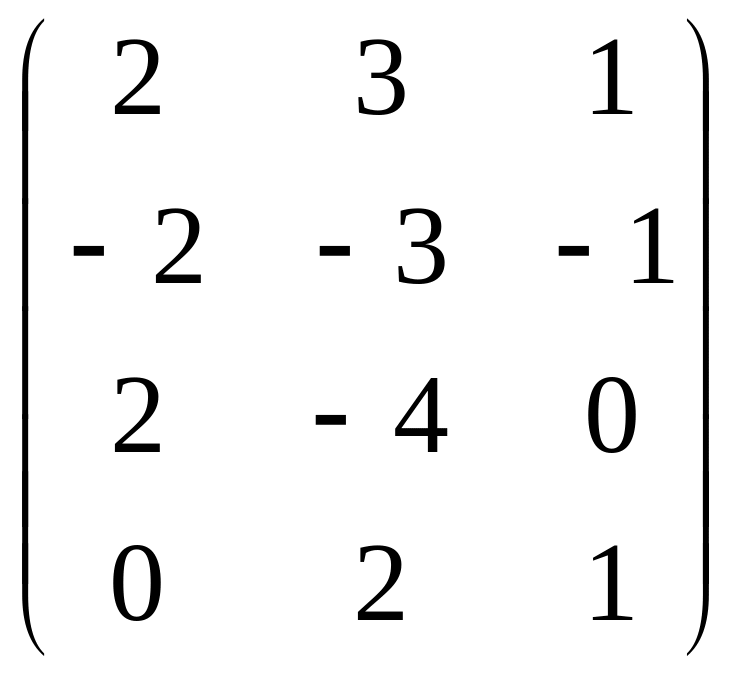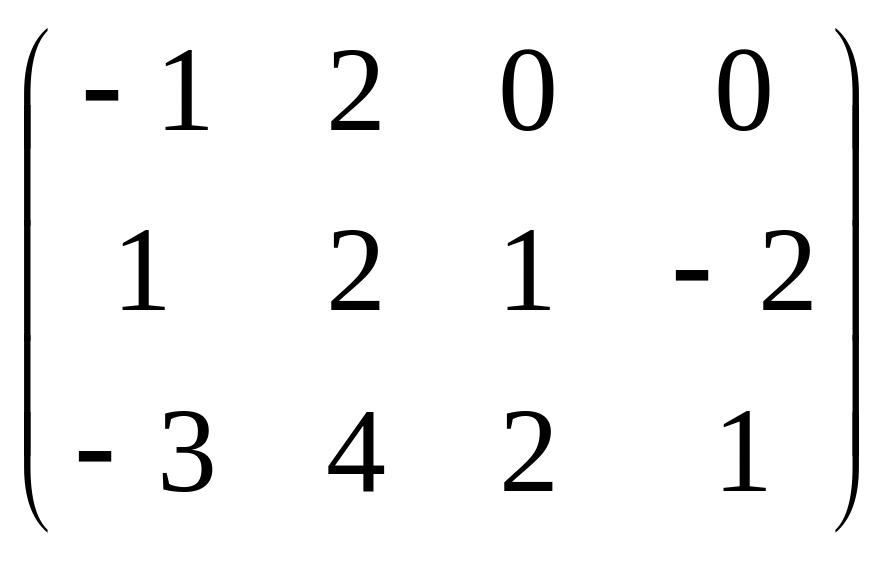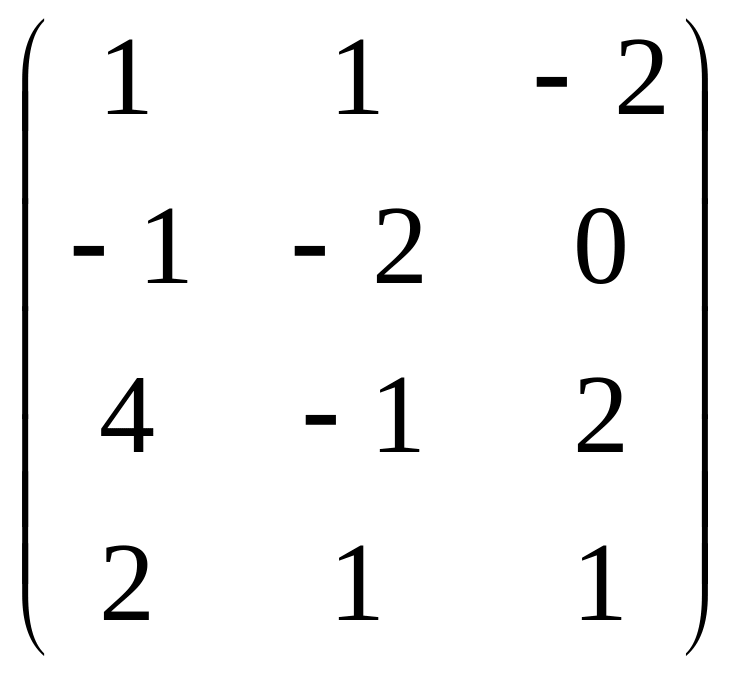Контрольная работа
по Математике (алгебра)
для студентов 1 курса заочного отделения
(преподаватель: Кириллова Д.А.)
(номер варианта соответствует номеру по списку в журнале старосты группы
на начало семестра)
Задание №1
Задана
матрица
.
Вычислите
и
.
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание №2
Даны матрицы
и число
.
Найдите матрицу
(единичную матрицу
написать подходящей размерности).
№ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
-2 |
|
|
|
|
|
3 |
|
|
|
|
|
-3 |
|
|
|
|
|
4 |
|
|
|
|
|
-4 |
|
|
|
|
|
5 |
|
|
|
|
|
-5 |
|
|
|
|
|
6 |
|
|
|
|
|
-6 |
|
|
|
|
|
2 |
|
|
|
|
|
-2 |
|
|
|
|
|
3 |
|
|
|
|
|
-3 |
|
|
|
|
|
4 |
Задание №3
Составить 2 матрицы второго порядка и 2 матрицы третьего порядка, вычислить их определители и их обратные матрицы.
Задание №4
Решите систему уравнений тремя способами: методом Гаусса, методом Крамера и с помощью обратной матрицы.
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
; |
|
|
; |
; |
|
|
; |
; |
|
|
; |
; |
|
|
; |
; |
|
|
. |
; |
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
;
;
Задание №5
Исследуйте систему на совместность. Если система совместна, найдите ее общее решение и одно частное решение. (Методом Гаусса)
;
;
;
;
;
;
;
;
;
;
;
;
;
;
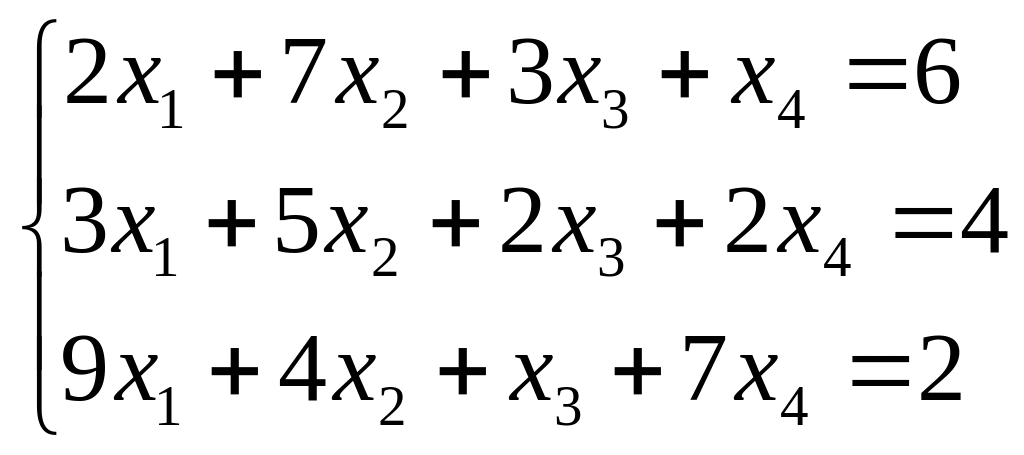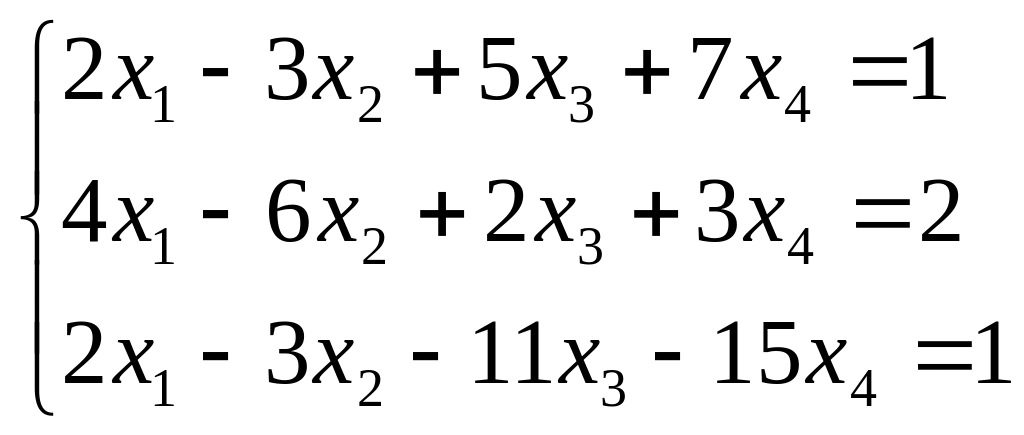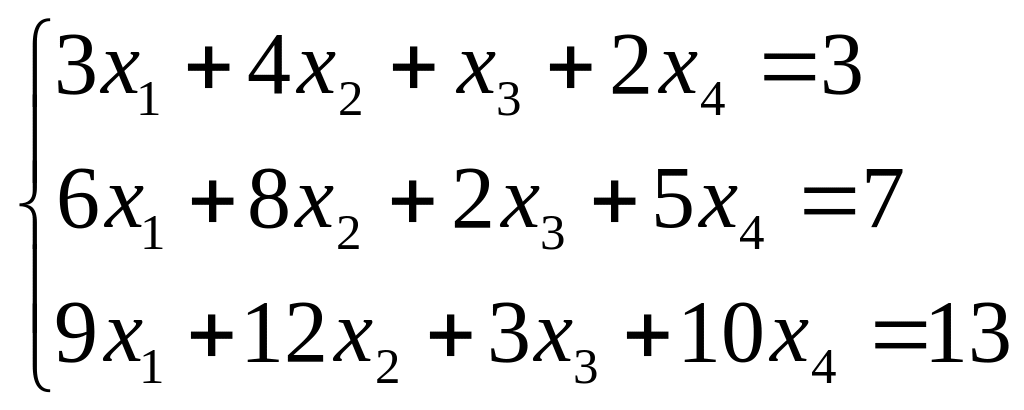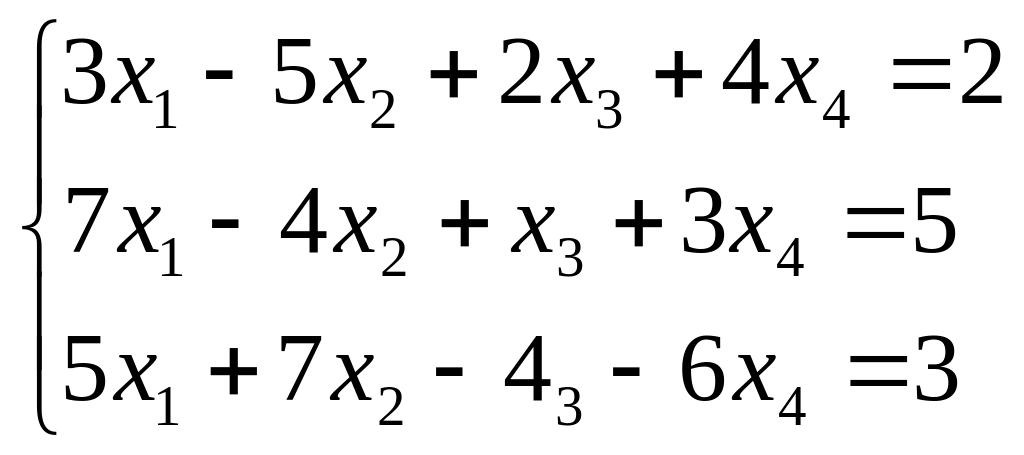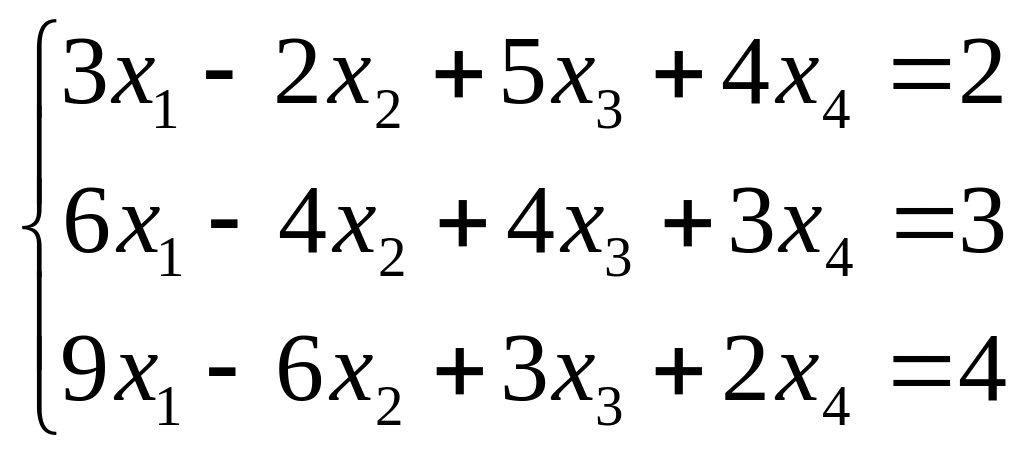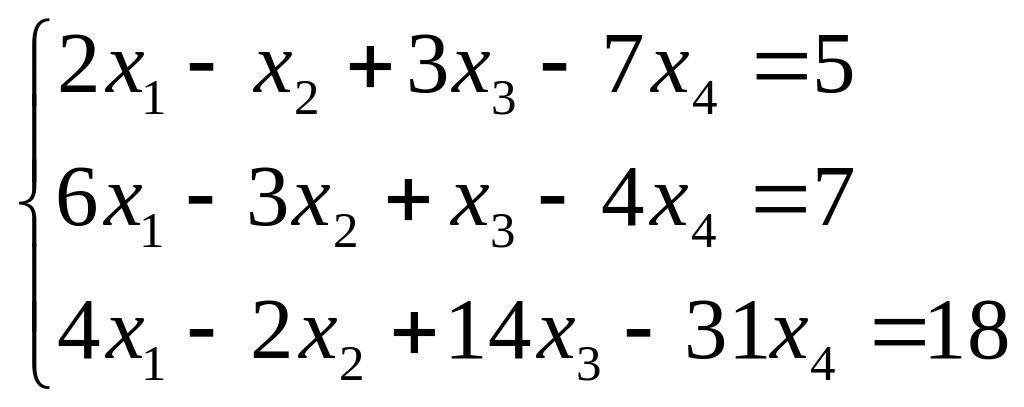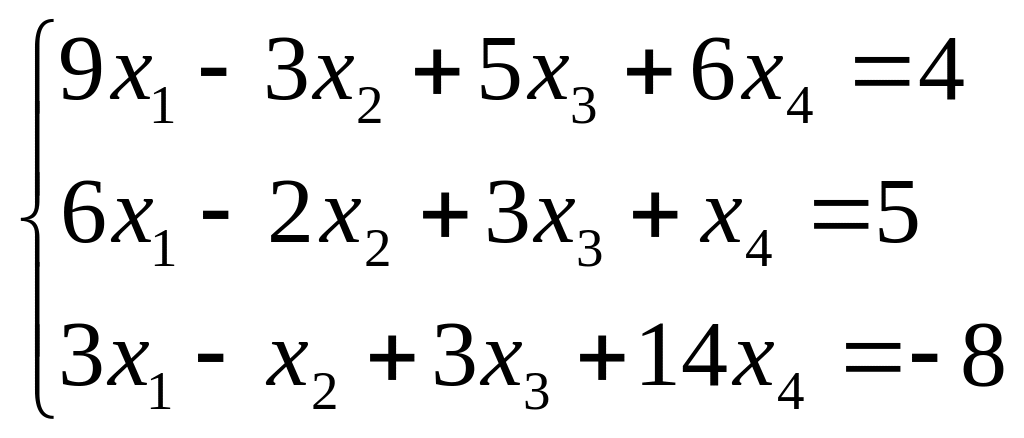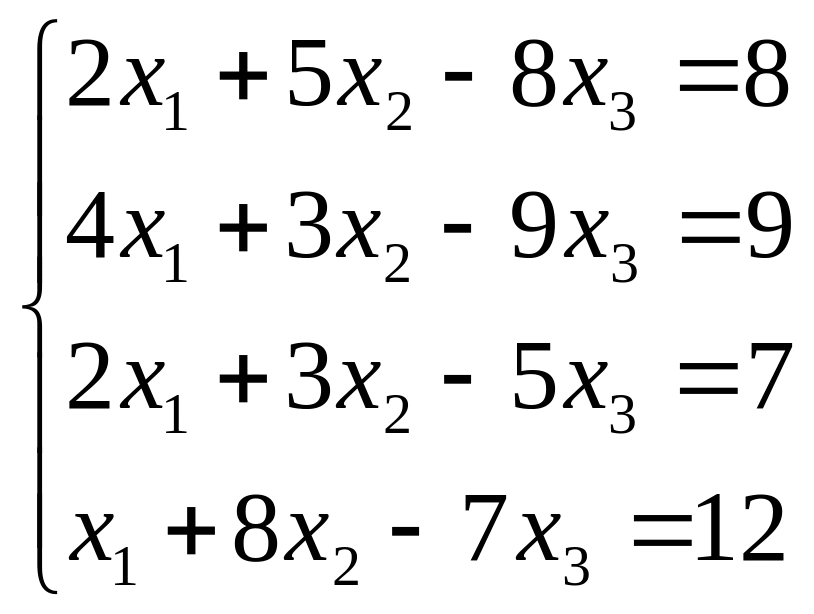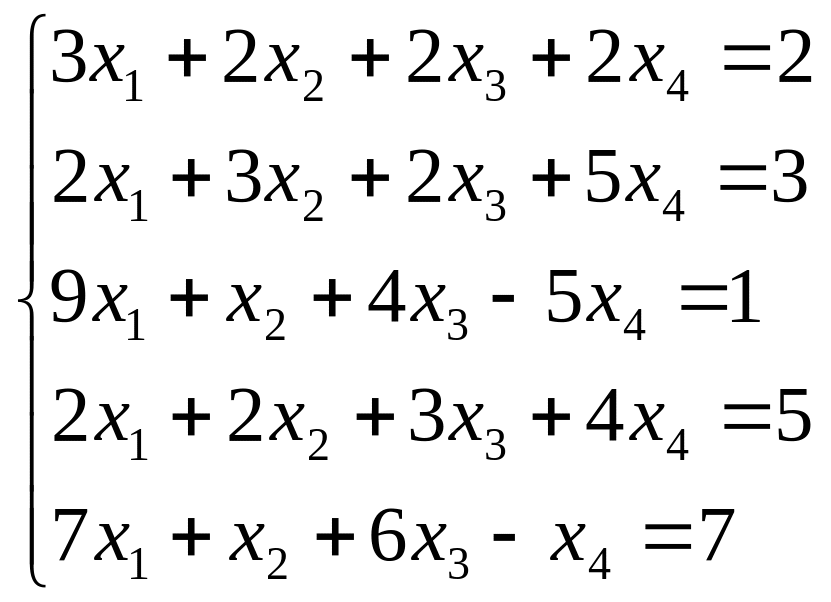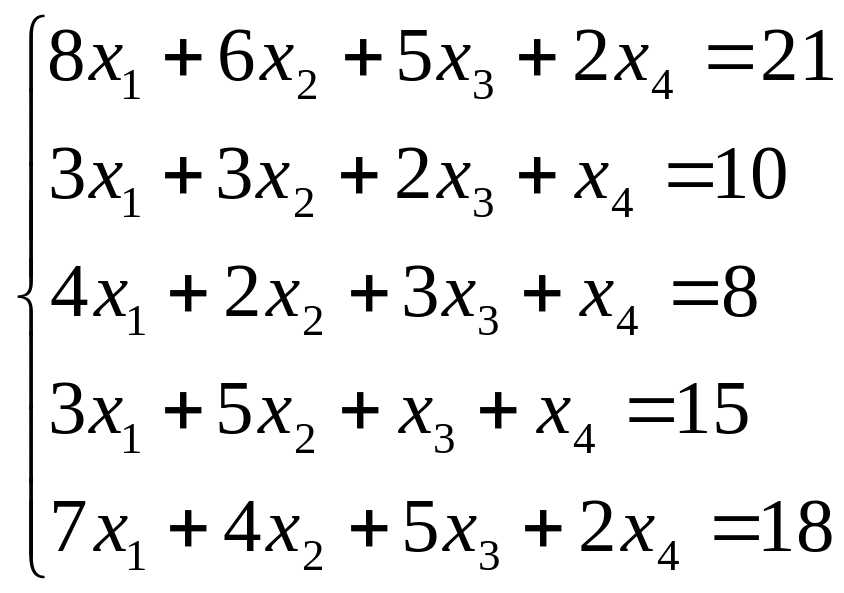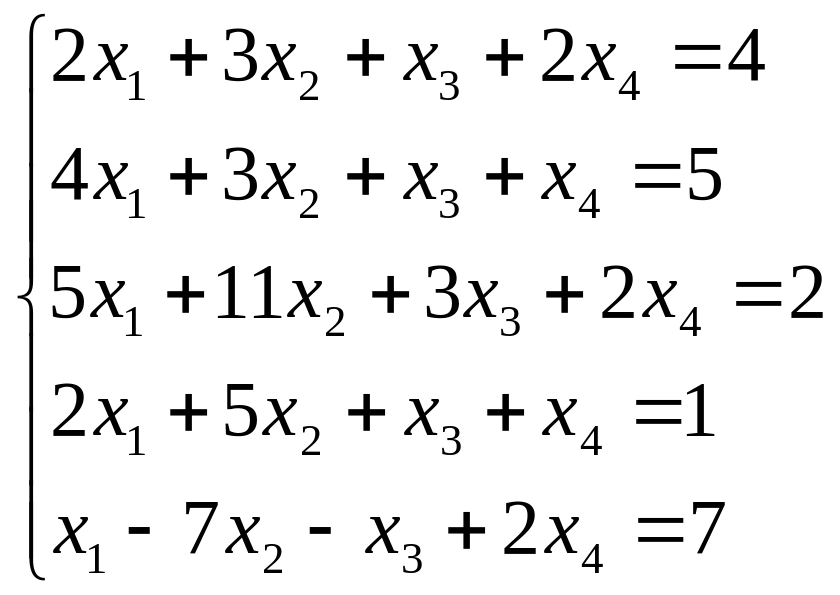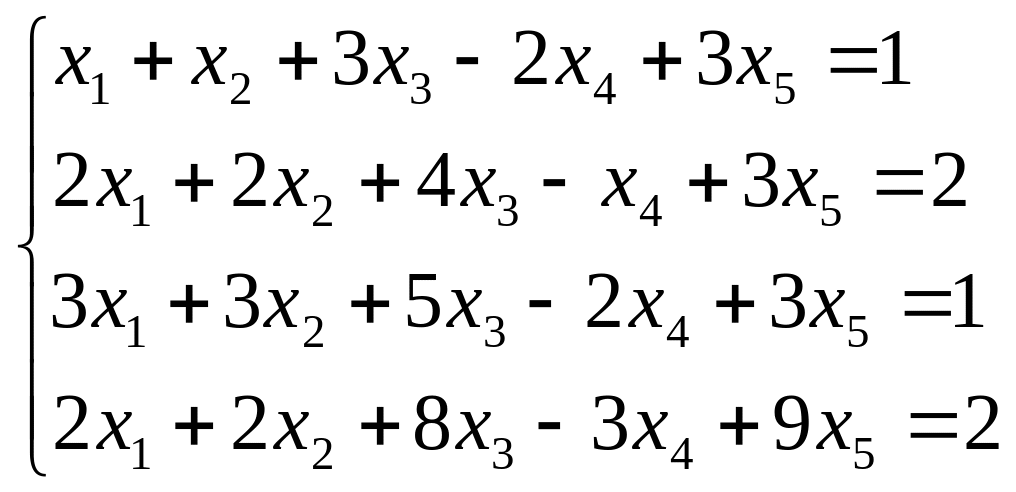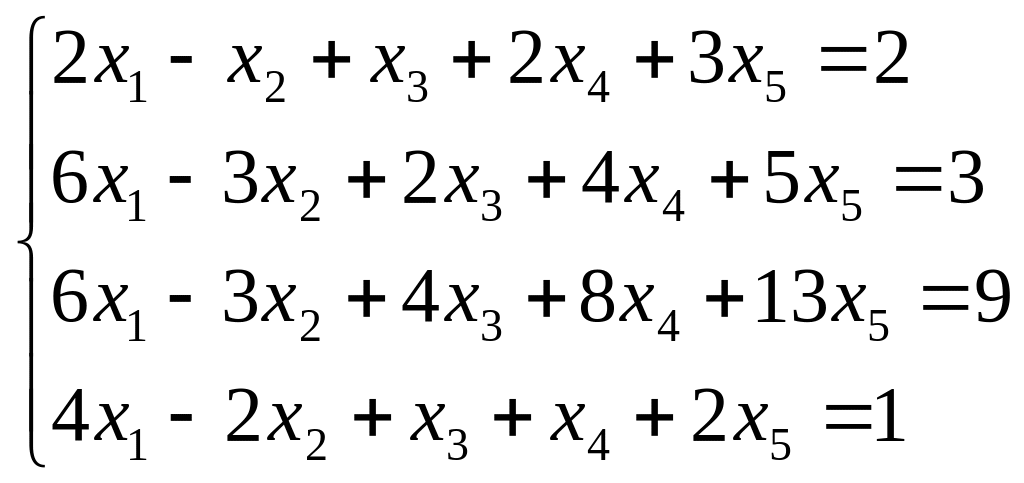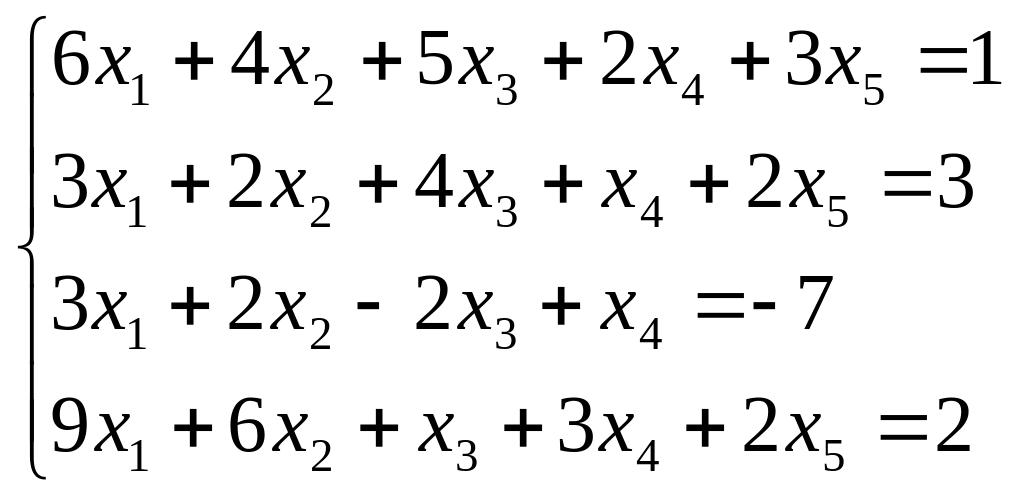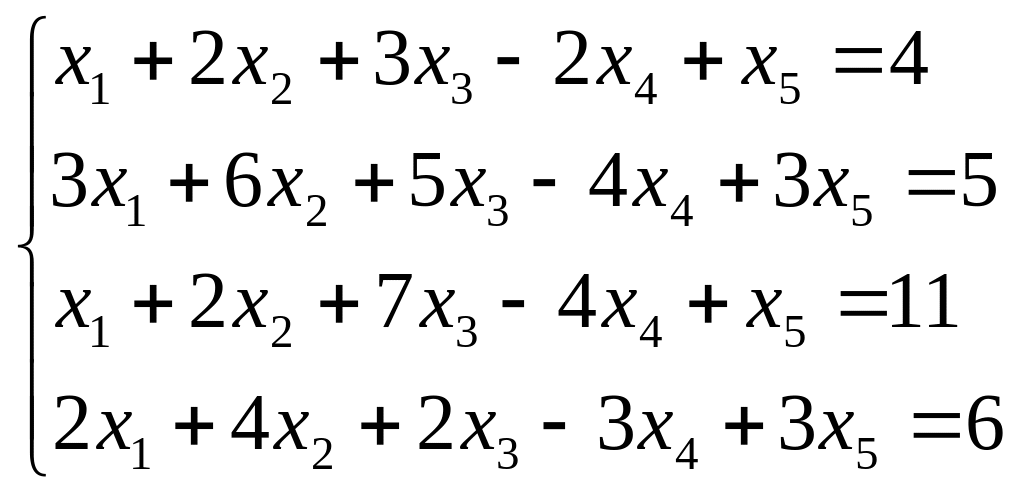
Задание №6
В
полярной системе координат задана
точка
.Декартова
система координат введена так, что
полюс полярной системы совпадает с
началом декартовой, а положительное
направление оси абсцисс совпадает с
направлением полярной оси. Определите
декартовы координаты точки
.
Сделайте чертеж и отметьте на нем
и
.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
2 |
3 |
4 |
5 |
2 |
3 |
4 |
5 |
2 |
3 |
4 |
5 |
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
