Основные формулы

По закону Кулона сила электростатического взаимодействия между двумя заряженными телами, размеры которых малы, по сравнению с расстоянием r между ними, определяется формулой

,

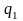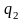где и - электрические заряды тел, ε – относительная диэлектрическая проницаемость среды, ε₀ = Ф/м – электрическая постоянная.

Напряженность электрического поля определяется формулой

,

где – сила, действующая на заряд q. Напряженность поля точечного заряда

.

По теореме Гаусса поток вектора напряженности сквозь любую замкнутую поверхность ,

где - алгебраическая сумма зарядов, находящихся внутри этой поверхности. При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами.

Напряженность поля, образованного заряженной бесконечно длинной нитью, ,

где - линейная плотность заряда на нити, а- расстояние от нити.

Напряженность поля, образованного заряженной бесконечной плоскостью, ,

где σ – поверхностная плотность заряда на плоскости.

Напряженность поля плоского конденсатора

.

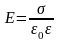Напряженность поля, образованного заряженным шаром,

,

_где q- заряд шара радиусом R, r- расстояние от центра шара, причем r≥R.

Примеры решения задач

Задача 1. Два одинаковых шарика, несущих равные заряды, подвешены на нитях равной длины к одной точке. Шарики опускают в керосин. Чему равна плотность материала шариков, если угол расхождения нитей в воздухе и в керосине одинаков? Плотность керосина ρ_к=0,8 г/см³, его диэлектрическая проницаемость ε = 2.

Решение: Когда система находится в воздухе, то на каждый шарик действует три силы (Рис.1.16 а): сила тяжести m сила натяжения нити и кулоновская сила _. Так как шарики находятся в равновесии, то сумма сил равна нулю:

.

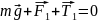Это означает, что при сложении сил векторы образуют прямоугольный треугольник (Рис.1,16. б). Из этого треугольника имеем: F₁ = mg tgα

Рисунок 1.16. К задаче 1 При погружении в керосин появляется

ещё архимедова сила F_a, а сила натяжения нити T₂ и кулоновская сила F₂ уменьшаются по модулю. Шарики находятся в равновесии, значит,

.

Отсюда следует, что

F₂ = (mg – F_a) tgα.

Отношение модулей сил и есть диэлектрическая проницаемость среды:

.

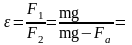
Отсюда

г/см³.

Задача 2. В атоме водорода электрон движется по стационарной круговой орбите с угловой скоростью 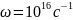. Определите радиус орбиты. Заряд электрона е =1,6 Кл, его масса m=9,1 кг.

Решение: В простейшей модели атома водорода считается, что электрон с зарядом -е движется по круговой орбите вокруг положительно заряженного ядра с зарядом +е. На электрон действует кулоновская сила притяжения к ядру F. Силой тяжести электрона можно пренебречь, так как она намного меньше F.

По второму закону Ньютона

,

Откуда

=1,4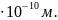

Задача 3. В сильном однородном электрическом поле напряженностью на одной силовой линии в точках 1 и 2, расположенных на расстоянии l₀ друг от друга, находятся протон р и электрон е. Начальная скорость обеих частиц равна нулю. Чему равно расстояние между частицами спустя время τ после начала движения?

Р ешение: Направим ось Х по направлению силовой линии , а начало отсчета совместим с точкой 2, где вначале находился электрон. Пренебрегая взаимодействием частиц друг с другом (сильное поле), можно считать движение электрона и протона равноускоренным. Тогда координата протона в момент времени τ равна:

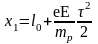, Рисунок 1.17.

где е- заряд, m_р- масса протона. К задаче 3

Координата электрона ,

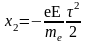где m_е- масса электрона. Искомое расстояние

,

так как m_р много больше m_е.

Задача 4. В вершинах квадрата со стороной a расположены два положительных и два отрицательных заряда, значение каждого из них Q (Рис.1.18 а, б). Определить напряжённость электрического поля в центре этого квадрата.

Решение: Поле создано четырьмя точечными зарядами. Поэтому напряжённость следует определять с помощью принципа суперпозиции:

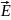= ₁+ ₂+ _{3 4}.

С начала следует показать на рисунке направление всех векторов _i зависящее от знака заряда Q_i.

Рисунок 1.18. К задаче 4

Расстояние от любого из зарядов до рассматриваемой точки

.

Рассмотрим распределение зарядов, показанное на рисунке 1.18 а. Напряжённости ₂ и ₄ полей, созданных вторым и четвёртым зарядами в точке С, сонаправлены и равны по модулю: E₂=E₄. Аналогично, E₁=E₃. Поэтому напряженность результирующего поля

Векторы ₁ и ₂ также равны по модулю и направлены ортогонально друг другу (по диагоналям квадрата), значит, результирующий вектор направлен вертикально вниз и тогда

E = 4E₁ cos 45^o.

Напряженность поля, созданного каждым из зарядов,

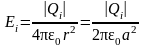
Заряд Q_i следует брать по модулю, так как знак каждого из зарядов был учтён при изображении соответствующего вектора _i. Окончательно

.

При расположении зарядов, показанном на рисунке 1.19 б, Е = 0.

Задача 5. Кольцо из проволоки радиусом R = 10 см имеет отрицательный заряд q = -5нКл. Найти напряжённости Е электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях L, равных 0, 5, 8, 10 и 15см. Построить график E = f(L). На каком расстоянии от центра кольца напряжённость Е электрического поля будет иметь максимальное значение?

Решение. Возьмем элемент кольца dl. Этот элемент имеет заряд dq. Напряженность электрического поля, заданная этим элементом в точке А, будет .

Вектор направлен по линии x, соединяющей точку А с элементом кольца dl (рис.1.19). Для нахождения напряженности поля всего кольца надо векторно сложить от всех элементов. Вектор d можно разло- жить на две составляющие d _n и d _τ. Составляющие d _n каждых двух диаметрально расположенных элементов взаимно уничтожаются, поэтому 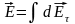. Но dE_τ=dEcosα= , что дает Рисунок 1.19. К задаче 5 .Учитывая, что , имеем

(1)

Если L>>R, то , т.е. на больших расстояниях заряженное кольцо можно рассматривать как точечный заряд.

Выразим величины x и L через угол α. Имеем R = x sinα, L = x cos α; теперь формула (1) примет вид sin²α. Для нахождения максимального значения напряженности Е возьмем производную и приравняем ее к нулю: 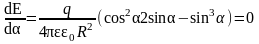или tg²α = 2. Тогда напряженность электрического поля имеет максимальное значение в точке А, расположенной на расстоянии см от центра кольца. Подставляя в (1) числовые данные, составим таблицу и построим график.

L, м	0	0,05	0,08	0,1	0,15
E, В/м	0	1600	1710	1600	1150

Задача 6. На некотором расстоянии от бесконечной равномерно заряженной плоскости плотностью σ = 0,1 нКл/см² положена круглая пластинка. Плоскость пластинки составляет с линиями напряженности угол 30^о. Определите поток Ф_Е вектора напряженности через эту пластинку, если ее радиус r равен 15 см.

Решение. Поток вектора напряженности Ф_Е через пластинку площадью равен

Ф_Е = E S cosα.

Н апряженность электростатического поля, создаваемого заряженной плоскостью (рис.1.20) с поверхностной плотностью заряда σ:

.

Площадь пластинки S = πr², где r – Рисунок 1.20. К задаче 6 радиус пластинки.

Угол α, образуемый нормалью к пластинке 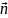и вектором равен 60^о. Следовательно,

.

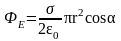Вывод: Напряженность является силовой характеристикой электрического поля. Она определяется зарядом – источником данного электрического поля и не зависит от пробного заряда q, внесенного в это поле. Очень важно определить правильно какой заряд является пробным, а какой является источником поля.