
- •Часть 2 «Электростатика. Постоянный ток»
- •1 Электростатика
- •1.1 Электрические заряды. Закон сохранения электрического заряда
- •1.2 Закон Кулона
- •1. 3 Электростатическое поле и его напряженность
- •1.4 Графическое изображение электростатических полей
- •1. 5 Принцип суперпозиции электростатических полей
- •1.6 Электростатическое поле электрического диполя
- •1.7 Поток вектора напряженности электростатического поля
- •1. 8 Теорема Гаусса для электростатического поля в вакууме
- •1. 9 Применение теоремы Гаусса для расчета напряженности электростатического поля
- •Поле двух бесконечных разноименно заряженных плоскостей.
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач).
- •Контрольные вопросы третьего уровня (тесты)
- •2.1 Работа сил электростатического поля при перемещении заряда
- •2.2 Циркуляция вектора напряженности электростатического поля
- •2.3 Потенциальная энергия и потенциал электростатического поля
- •2.4 Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности
- •2.5 Вычисление разности потенциалов по напряженности поля
- •Контрольные вопросы первого уровня
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы третьего уровня (тесты)
- •3 Диэлектрики в электрическом поле
- •3.1 Типы диэлектриков. Поляризация диэлектриков
- •3.2 Вектор поляризации и диэлектрическая восприимчивость диэлектриков
- •3.3 Напряженность поля в диэлектрике
- •3.4. Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
- •3.5 Сегнетоэлектрики
- •3.6 Пьезоэлектрический эффект
- •3.7 Проводники в электростатическом поле
- •3.8 Электрическая емкость уединенного проводника
- •3.9 Взаимная электроемкость. Конденсаторы
- •3.10 Энергия заряженного уединенного проводника, конденсатора. Энергия электростатического поля
- •Контрольные вопросы первого уровня
- •Методика решения задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы второго уровня (сборник задач)
- •Контрольные вопросы третьего уровня (тесты)
- •4.1 Электрический ток, сила и плотность тока
- •4.2 Сторонние силы. Электродвижущая сила и напряжение
- •4.3 Закон Ома для участка и полной замкнутой цепи
- •4.4 Сопротивление проводника. Явление сверхпроводимости
- •4.5 Работа и мощность тока. Закон Джоуля-Ленца
- •4.6 Правила Кирхгофа для разветвленных цепей
- •Контрольные вопросы первого уровня
- •Методические указания по решению задач
- •Основные формулы
- •Примеры решения задач
- •Контрольные вопросы третьего уровня (сборник задач).
- •Контрольные вопросы третьего уровня (тесты)
1. 5 Принцип суперпозиции электростатических полей
Основной
задачей электростатики является
определение величины и направления
вектора напряженности
в каждой точке поля, создаваемого либо
системой неподвижных точечных зарядов,
либо заряженными поверхностями
произвольной формы. Рассмотрим первый
случай, когда поле создано системой
зарядов q1,
q2,...,
qn.
Если в какую-либо точку этого поля
поместить пробный заряд q0,
то на него со стороны зарядов q1,
q2,...,
qn
будут действовать кулоновские силы
 .
Согласно принципу независимости действия
сил, рассмотренного в механике,
равнодействующая сила
.
Согласно принципу независимости действия
сил, рассмотренного в механике,
равнодействующая сила
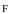 равна их векторной сумме
равна их векторной сумме
 .
.
Используя
формулу напряженности электростатического
поля, левую часть равенства можно
записать:
 ,
где
- напряженность результирующего поля,
создаваемого всей системой зарядов в
точке, где расположен пробный заряд q0.
Правую часть равенства соответственно
можно записать
,
где
- напряженность результирующего поля,
создаваемого всей системой зарядов в
точке, где расположен пробный заряд q0.
Правую часть равенства соответственно
можно записать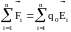 ,
где
,
где
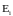 - напряженность поля, создаваемая одним
зарядом qi.
Равенство примет вид
- напряженность поля, создаваемая одним
зарядом qi.
Равенство примет вид
 .
Сокращая на q0,
получим
.
Сокращая на q0,
получим
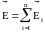 .
.
Напряженность электростатического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности. В этом заключается принцип независимости действия электростатических полей или принцип суперпозиции полей.
Обозначим
через
 радиус-вектор, проведенный из точечного
заряда qi
в исследуемую точку поля. Напряженность
поля в ней от заряда qi
равна
радиус-вектор, проведенный из точечного
заряда qi
в исследуемую точку поля. Напряженность
поля в ней от заряда qi
равна
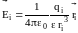 .
Тогда результирующая напряженность
,
создаваемая всей системой зарядов равна
.
Тогда результирующая напряженность
,
создаваемая всей системой зарядов равна
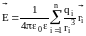 .
Полученная формула применима и для
расчета электростатических полей
заряженных тел произвольной формы, так
как любое тело можно разделить на очень
малые части, каждую из которых можно
считать точечным зарядом qi.
Тогда расчет
в любой точке пространства будет
аналогичен выше приведенному.
.
Полученная формула применима и для
расчета электростатических полей
заряженных тел произвольной формы, так
как любое тело можно разделить на очень
малые части, каждую из которых можно
считать точечным зарядом qi.
Тогда расчет
в любой точке пространства будет
аналогичен выше приведенному.
1.6 Электростатическое поле электрического диполя
Электрический
диполь -
система
двух равных по модулю и противоположных
по знаку точечных зарядов +q
и -q,
расстояние l
между которыми
мало по сравнению с расстоянием до
исследуемых точек поля. Прямая, проходящая
через оба заряда, называется осью диполя.
Вектор
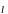 ,
направленный по оси диполя от
отрицательного заряда к положительному
и по модулю равный расстоянию между
ними, называется плечом
диполя.
Вектор, совпадающий по направлению с
плечом диполя и равный произведению
модуля заряда
,
направленный по оси диполя от
отрицательного заряда к положительному
и по модулю равный расстоянию между
ними, называется плечом
диполя.
Вектор, совпадающий по направлению с
плечом диполя и равный произведению
модуля заряда
 на плечо
,
называется электрическим
м
на плечо
,
называется электрическим
м

Рисунок 1.4 - Электрический диполь
оментом диполя или дипольным моментом
 .
Силовые линии поля диполя также
представлены на рисунке 1.4.
.
Силовые линии поля диполя также
представлены на рисунке 1.4.
Изучение поля диполя представляет большой практический интерес, так как молекулы диэлектриков по своим электрическим свойствам подобны диполям. Определяя напряженность электрического поля диполей, можно рассчитать силу электрического взаимодействия между молекулами, которая позволяет объяснить некоторые свойства и особенности поведения диэлектриков.
Рисунок
1.5 - К определению напряженности поля
на оси диполя.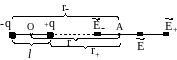
 ,
где
,
где
 и
и
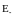 - напряженности полей зарядов +q
и -q.
Если исследуемая точка А расположена
на оси диполя (рис.1.5), то векторы
и
направлены вдоль оси, но в противоположные
стороны.
- напряженности полей зарядов +q
и -q.
Если исследуемая точка А расположена
на оси диполя (рис.1.5), то векторы
и
направлены вдоль оси, но в противоположные
стороны.
Модуль
вектора
равен
 ,
где
,
где
 ,
, 
В приведенных формулах =1 (воздух, вакуум).
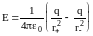 .
Выражение в скобке приведем к общему
знаменателю и разложим разность
квадратов:
.
Выражение в скобке приведем к общему
знаменателю и разложим разность
квадратов:
 .
.
Из
рисунка видим, что
 ;
;
 ,
где r
- расстояние от центра плеча диполя О
до точки А. Так как по определению диполя
rl,
то
,
где r
- расстояние от центра плеча диполя О
до точки А. Так как по определению диполя
rl,
то
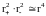 .
Таким образом, выражение для Е
принимает вид:
.
Таким образом, выражение для Е
принимает вид:
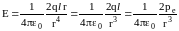
В
векторной форме:
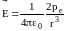 .
.
