Н.Ф. Рожков, д.В. Березовский, м.Г. Родионов

__________________________________________________________________

МЕТОДИЧЕСКОЕ УКАЗАНИЕ К РЕШЕНИЮ ЗАДАЧ

ПО ДИСЦИПЛИНЕ

"ПРЕОБРАЗОВАНИЕ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ"

ОмГТУ-2005

Данное методическое указание предназначено для проверки знаний студентов 3-го курса специальности "Информационно-измерительной техники и технологий" по дисциплине "Преобразование измерительных сигналов" в форме решения задач по разделам: "Квантование", "Модуляция", "Динамические погрешности", "Кодирование". Методическое указание содержит краткую теорию по каждому разделу, контрольные задачи и список рекомендуемой литературы.

Авторы: Рожков Н.Ф., Березовский Д.В., Родионов М.Г.

1. Квантование

1.1. Квантование с точки зрения теории информации

Преобразование непрерывных сигналов в дискретные называют квантованием сигналов. Дискретизация сигналов позволяет применить:

1. Временное разделение каналов, что позволяет увеличить пропускную способность линий связи

2. Повышать помехоустойчивость при передаче информации, что позволяет получить большую точность передаваемых сообщений

3. Устранить избыточность при передаче информации, а также использовать при построении цифровых измерительных приборов.

Различают квантование по уровню, по времени, а также по уровню и времени.

Погрешность квантования при равномерном квантовании по уровню определятся как:

,

где - погрешность квантования,

- квантованное значение,

- действительное значение.

Закон распределения этой погрешности зависит от закона распределения х(t).

Математическое ожидание суммарной погрешности квантования .

Дисперсия погрешности:

Таким образом, в случае отсутствия фиксации дискретных уровней относительно начального уровня квантуемой функции среднеквадратическая погрешность квантования увеличивается в раза.

При квантовании по времени дискретизация сигнала x(t) связана с заменой промежутка изменения независимой переменной некоторым множеством точек, то есть операции дискретизации соответствует отображение.

При малых интервалах дискретизации количество отсчетов на заданном интервале будет большим, а, следовательно, точность восстановления исходной функции будет высокой. И наоборот, при больших интервалах tколичество отсчетов уменьшается и точность воспроизведения уменьшается.

Методы дискретизации классифицируют по следующим наиболее существенным признакам:

1. Регулярность отсчетов: равномерная, неравномерная, случайная, аддитивная, с кратными интервалами, с некратными интервалами

2. Критерий оценки точности: максимальный, среднеквадратический, интервальный, вероятностнозональный

3. Базисные функции: ряд Фурье, ряд Котельникова, полином Чебышева, полином Лежандра, степенные полиномы, функции Уолша, функции Хаара

4. Принцип приближения: интерполяция, экстраполяция, комбинированный.

Интервал дискретизации для значений максимальной относительной погрешности при ступенчатой аппроксимации определяется как:

,

где t– интервал дискретизации,

_max– максимальная относительная погрешность,

_с– наивысшая частота сигнала.

Для случая кусочно-линейной интерполяции:

.

Для параболической:

,

М₃– модуль максимума 3-й производной.

Пример1.

Дан сигнал вида Ux=Um*sin2πFt, имеющийUm=1 В,Fmax= 100 Гц, Определить шаг квантования, число преобразований в секунду для случая линейной аппроксимации, если допустимая абсолютная погрешность восстановления не превышает 0,1 В.

Решение.

Интервал дискретизации для значений максимальной относительной погрешности при линейной аппроксимации определяется как:

Подставляем известные значения в формулу и получим:

Шаг квантования можно определить как:

При рассмотрении элементов теории информации при квантовании сигнала оперируют случайными величинами (Рисунок 1).

Рисунок 1 – Сообщения с равновероятными и независимыми распределениями уровней квантования

Отображается некоторые сообщения, поступающие от источника информации. При этом сигнал квантуется по уровню и времени, имеющий n– различных состояний. Тогда вероятность любого из уровней (n> 1) сигнала любого из отсчетов (m= 1) может быть выражена:, гдеи. Количество информации в этом случае приn>>1 иm=1:

.

При m=2,n>>1:

.

А для условия m>>1,n>>1:

Если количество источников сообщения будет равно k, то:

.

Энтропия – это количество информации, приходящиеся на один отчет.

.

Пример2.

Пусть имеется два потенциометрических датчика D1,D2, погрешность составляет 0.1% и 0.2%, соответственно. Определить количество информации, если первым датчиком снято 4 отсчета, вторым – 6. Определить энтропию и пропускную способность как максимальную скорость, которая составляет скорость информации от каждого датчика 0.1 секунды за отсчет.

Решение.

1. Для того, чтобы определить количество информации, сначала необходимо вычислить количество состояний каждого из датчиков.

,

тогда количество информации будет:

2. Энтропия определяется как:

Тогда:

3. Пропускная способность определяется как: .

Тогда

Рассмотрим теперь сообщения с неравномерными уровнями квантования и независимыми отсчетами (Рисунок 2). Пусть при передачи сообщения снимается m– независимых друг от друга отсчетов, однако в отличие от первого случая уровни квантования появляются неравновероятно с вероятностямиP(S₀),P(S₁)…P(S_n). При этом, еслиm>>1, то одни и те же уровни квантования могут появляться неоднократно, то естьS₀=n₀– раз,S₁=n₁– раз так далее.

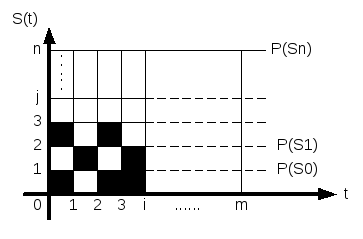
Рисунок 2 – Сообщения с неравномерными уровнями квантования и независимыми отсчетами

Определим теперь количество информации и энтропию для случая, когда m>>1, аn=2. Допустим, что при достаточно длинной последовательности значения уровня сигналаS₀встречаетсяn₀– раз, аS₁–n₁ – раз, тогда вероятности появленияS₀иS₁можно выразить через частности вероятностей,, где. Приведенное выше сведем в таблицу 1.

Таблица 1 – Параметры сообщения с неравномерными уровнями квантования и независимыми отсчетами

Количество отсчетов	m
Уровни квантования	S0	S1
Вероятности появления	P(S0)	P(S1)
Число уровней	k0	k1
Частота появления
Выполнение условия

Если обозначить m– длина команды, а М – число команд, полагая, что команды независимы друг от друга, то вероятность появления команды определяется. С другой стороны на основании теории вероятности о совмещении двух событий. Рассматривая, по условию, команды как сообщения с равновероятным и независимым распределением, определим количество информации:

Соответственно энтропия:

Пример3.

Пусть каждая команда управления передается 10-ти разрядным двоичным кодом. Причем каждая команда состоит из 4-х нулей и 6-ти единиц. Определить вероятность появления команд, количество информации и энтропию.

Решение.

Данные: m= 10,k₀= 4,k₁= 6,m= 4 + 6 = 10.

Определим:

1. Вероятность появления команд:

,

Тогда вероятность появления команд на основе теоремы теории вероятности и совмещении двух событий:

2. Количество информации в каждой команде:

3. Определим энтропию как:

Рассмотрим сообщения с неравновероятным и зависимым распределением уровней сигнала. В реальном случае символы, образующие сообщение, взаимосвязаны, что необходимо учесть в выражении энтропии. Величина энтропии с учетом взаимосвязи может быть выражена по аналогии с первыми двумя случаями.

.

Соответственно, для 2-х символов:

Для 3-х символов:

Пример4.

Управляющее устройство вырабатывает три командыS₁,S₂,S₃. При этом известны вероятности их появленияP(S₁) = 0.3,P(S₂) = 0.6,P(S₃) = 0.1 и взаимосвязь между любыми командами, то есть задаются условные вероятности перехода от одной команды к другой. Данные сведем в таблицу.

Si	Sj
	S1	S2	S3
S1	0.8	0	0.2	1
S2	0	0.5	0.5	1
S3	0.1	0.5	0.4	1

Решение.

Определим энтропию и избыточность команд для всех трех случаев.

1. Для 1-го случая: энтропия будет равна:

,

избыточность определяется:

,

так как уровни равновероятны и потому избыточность равна нулю.

2. Для второго случая:

3. Для третьего случая:

.

Определим вероятности с учетом условного перехода, которые сведем в таблицу.

Si	Sj
	S1	S2	S3
S1	0.24	0	0.06	0.3
S2	0	0.3	0.3	0.6
S3	0.01	0.15	0.04	0.1

Коэффициент избыточности:

Как видно из примера, коэффициент избыточности возрастает и для третьего случая он самый большой.