§4. Дифференциальные зависимости между поперечной силой и изгибающим моментом. Пункты контроля правильности построения эпюр внутренних силовых факторов

Рассмотрим брус, нагруженный произвольно распределенной нагрузкой (рисунок 4.1).

Двумя сечениями вырежем из бруса бесконечно малый участок длиной dz. В этом случае действующую внешнюю нагрузку можно считать равномерно распределенной, или постоянной.

Составляем уравнение равновесия для этого бесконечно малого участка:

(4.1)*

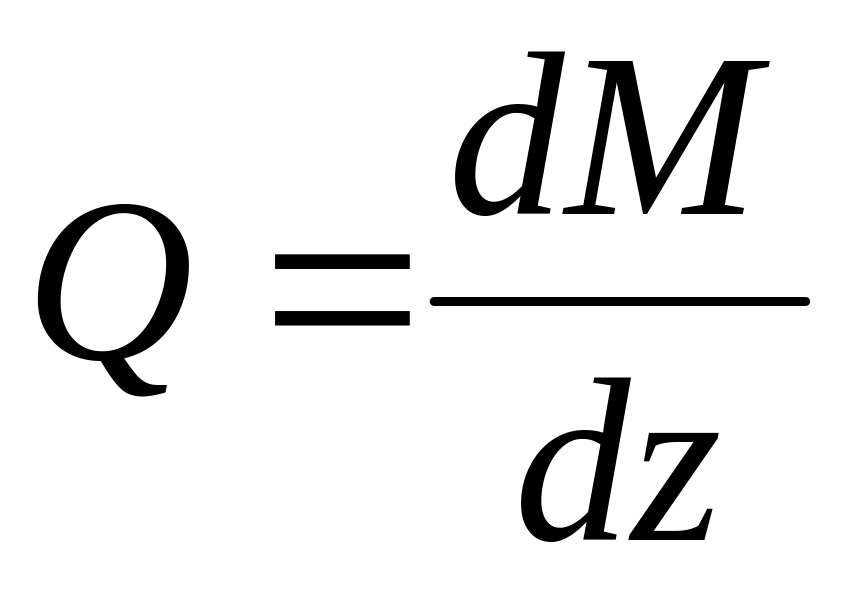
(4.2)*

Подставим (4.2) в (4.1), получим:

(4.3)*

Система уравнений (4.1), (4.2) и (4.3) носит название дифференциальных зависимостей при изгибе. При помощи этих зависимостей можно выполнить проверку правильности построения эпюр при изгибе.

Рассмотрим основные пункты контроля построения эпюр В.С.Ф. для случая изгиба:

1. На участках, где действует только внешний момент, эпюра Q отсутствует, а эпюра M ограничена прямой, параллельной оси эпюры (рисунок 4.2).

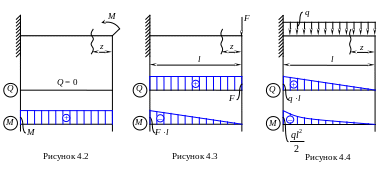
2. На участках, где действует только сила, эпюра Q ограничена прямой, параллельной оси, а эпюра M – наклонной линией (рисунок 4.3).

3. На участках, где действует только равномерно распределенная нагрузка, эпюра Q ограничена наклонной, а эпюра M – параболой, причем кривизна параболы совпадает с направлением стрелок распределенной нагрузки. Это утверждение справедливо только для растянутого волокна. (рисунок 4.4).

4. В сечениях, где приложен внешний момент, эпюра Q остается неизменной, а ан эпюре M наблюдается «скачки» на величину внешнего момента (рисунок 4.5).

5. В сечениях, где приложена внешняя сила, на эпюре Q наблюдается «скачок» по направлению и величине внешней силы, а на эпюре M возникает излом линии, острие которого (излома) совпадает с направлением внешней силы, если эпюра построена на растянутом волокне.

6. В сечениях, где эпюра Q пересекает осевую линию, то есть обращается в нуль, на эпюре M имеет место экстремальный момент, то есть максимальный или минимальный в пределах данного участка (рисунок 4.7).

7. На участках, где Q больше нуля, ординаты эпюры M слева направо возрастают алгебраически, а где Q меньше нуля – убывают (рисунки 4.3 – 4.7).

8. Ординаты эпюры Q изменяются прямо пропорционально тангенсу угла наклона касательной к эпюре моментов в данной точке (рисунок 4.7, увеличенное изображение).

§5. Построение эпюр для сложных балок, рам и криволинейных брусьев

Под сложной понимается балка, опирающаяся более чем на две опоры, имеющая в своем составе врезанные шарниры (рисунок 5.1).

При решении сложных балок необходимо составить дополнительные уравнения в виде уравнений моментов относительно врезанного шарнира для одной из частей балки, а при построении эпюр моментов необходимо учесть то, что в данном сечении с врезанным шарниром момент должен иметь нулевую ординату.

Рамой называется система, состоящая из прямолинейных стержней, соединенных жесткими узлами (рисунок 5.2).

Построение эпюр для рам выполняется также, как для балок, но с учетом следующих особенностей:

1. для рамы строится не две, а три эпюры – продольной, поперечной сил (N и Q) и изгибающего момента (M);

2. для эпюр N и Q принимаются такие же правила знаков как для балок, но при построении эпюр положительные ординаты откладываются снаружи рамы, а отрицательные – внутри ее;

3. правила знаков для изгибающего момента принимаются условно, например, против часовой стрелки «+», против часовой стрелки «–», но, несмотря на это, сама эпюра строится на растянутом или сжатом волокне без указания знака;

4. построенные эпюры N, Q и M проверяются путем вырезания узлов и проверки их равновесия под действием внутренних силовых факторов и внешних нагрузок (если равновесие узла обеспечивается – эпюра построена правильно!).

При построении эпюр для криволинейных стержней, например арок, все уравнения В.С.Ф. составляются в угловых координатах, то есть через переменный угол, тогда получаемые эпюры также будут иметь криволинейные очертания (рисунок 5.3).