Повторні випробування за схемою Бернуллі

1. Схема повторних незалежних випробувань (схема Бернуллі).

2. Найімовірніше число появи випадкової події у схемі Бернуллі.

3. Локальна терема Муавра-Лапласа.

4. Інтегральна теорема Муавра-Лапласа.

5. Гранична теорема Пуассона.

Завдання 1. Ймовірність появи події в кожному випробуванні дорівнює Знайти ймовірність того, що при випробуваннях подія з’явиться:

1) разів;

2) від до разів;

3) не більше разів.

№ варіанта
1	0,6	100	70	40	50	60
2	0,7	200	120	100	150	180
3	0,75	300	200	230	250	150
4	0,8	400	250	200	300	100
5	0,65	100	50	60	70	55
6	0,55	200	130	140	160	100
7	0,5	300	200	220	250	150
8	0,85	400	300	320	350	200
9	0,9	100	60	80	90	75
10	0,68	200	140	100	120	90

Випадкові величини

1. Поняття випадкової величини (ВВ). Приклади випадкових величин. Закон розподілу випадкової величини .

2. Дискретні випадкові величини (ДВВ).

3. Неперервні випадкові величини (НВВ). Щільність ймовірностей, її властивості.

4. Функція розподілу випадкової величини, її властивості та графік.

5. Математичне сподівання випадкової величини.

6. Мода та медіана випадкової величини.

7. Дисперсія та середнє квадратичне відхилення випадкової величини.

8. Моменти розподілу випадкової величини.

Завдання 1.

Ймовірність того, що радіосигнал буде прийнятий при кожній з 6 передач, дорівнює

1) Побудувати закон розподілу випадкової величини – кількості прийнятих радіосигналів.

2) Побудувати функцію розподілу ймовірностей і накреслити її графік.

3) Знайти математичне сподівання , дисперсію , середнє квадратичне відхилення .

4) Знайти моду .

5) Знайти

№ варіанта	1	2	3	4	5	6	7	8	9	10
р	0,6	0,7	0,65	0,55	0,75	0,85	0,72	0,82	0,4	0,5

Завдання 2. Для непарних .

Випадкова величина задана функцією розподілу . Знайти:

1) параметр

2) диференціальну функцію (щільність розподілу),

3) математичне сподівання , дисперсію середнє квадратичне відхилення ,

4) моду та медіану ,

5)

Побудувати графіки функції та щільності розподілу.

1. 3.

7.

9.

Завдання 2. Для парних .

Виппадкова величина задана щільністю розподілу . Знайти:

1) параметр

2) інтегральну функцію розподілу,

3) математичне сподівання , дисперсію середнє квадратичне відхилення ,

4) моду та медіану

5)

Побудувати графіки функції розподілу та щільності розподілу.

2.

4.

6.

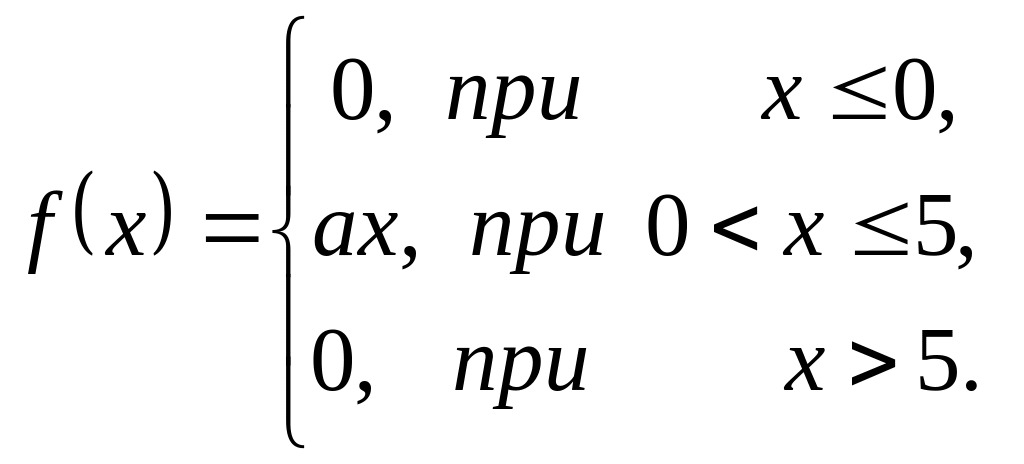
8.

10.

9. Нормальний закон розподілу, його числові характеристики. Правило трьох сигм.

Завдання 3. Випадкова величини розподілена нормально, її математичне сподівання дорівнює , а середнє квадратичне відхилення Знайти ймовірність того, що матиме значення в інтервалі .